Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Cohen, S. D.
1975.
Dense primitive polynomial sequences.
Mathematika,
Vol. 22,
Issue. 1,
p.
89.
Sárközy, A.
1997.
The Mathematics of Paul Erdös I.
Vol. 13,
Issue. ,
p.
241.
Sárközy, András
2013.
The Mathematics of Paul Erdős I.
p.
221.
Kartika, Nurmayuni
Sukenda, Sukenda
Nuryati, Sri
Lusiastuti, Angela Mariana
and
Hidayatullah, Dendi
2022.
Monovalent Mycobacterium fortuitum oral vaccination on giant gourami (Osphronemus Goramy) to prevent mycobacteriosis.
Aquaculture International,
Vol. 30,
Issue. 6,
p.
2775.

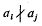 whenever
whenever