Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Öke, Figen
2009.
On Extensions of Valuations with given Residue Field and Value Group.
Mathematika,
Vol. 55,
Issue. 1-2,
p.
191.

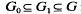 is an inclusion of totally ordered abelian groups with [
is an inclusion of totally ordered abelian groups with [