Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-13T08:29:36.118Z Has data issue: false hasContentIssue false
  • English
  • Français

Ramanujan's explicit values for the classical theta-function

Part of: Other special functions

Published online by Cambridge University Press:  26 February 2010

Bruce C. Berndt  and
Heng Huat Chan
Bruce C. Berndt
Affiliation:
Department of Mathematics, University of Illinois, 1409 West Green Street, Urbana, IL 61801, U. S. A.
Heng Huat Chan
Affiliation:
School of Mathematics, Institute for Advanced Study, Princeton, NJ 08540, U.S.A.
Get access

Extract

Let

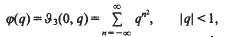
where φ is the notation used by Ramanujan in his notebooks [15], and is the familiar notation of Whittaker and Watson [20, p. 464]. It is well known that [1, p. 102] (with a misprint corrected)

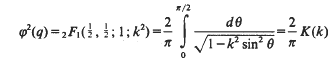
where 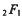denotes the ordinary or Gaussian hypergeometric function; k, 0 < k < 1, is the modulus; K is the complete elliptic integral of the first kind; and

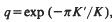
where K′=K(k′) and 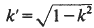is the complementary modulus. Thus, an evaluation of any one of the functions φ, 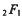, or K yields an evaluation of the other two functions. However, such evaluations may not be very explicit. For example, if K(k) is known for a certain value of k, it may be difficult or impossible to explicitly determine K′, and so q cannot be explicitly determined. Conversely, it may be possible to evaluate φ(q) for a certain value of q, but it may be impossible to determine the corresponding value of k. (Recall that 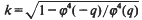[1, p. 102].)

MSC classification

Secondary: 33E05: Elliptic functions and integrals
Type
Research Article
Information
Mathematika , Volume 42 , Issue 2 , December 1995 , pp. 278 - 294
Copyright
Copyright © University College London 1995

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Berndt, B. C.. Ramanujan's Notebooks, Part III (Springer-Verlag, New York, 1991).Google Scholar
2.Berndt, B. C.. Ramanujan's Notebooks, Part IV (Springer-Verlag, New York, 1994).CrossRefGoogle Scholar
3.Berndt, B. C., Bhargava, S. and Garvan, F. G.. Ramanujan's theories of elliptic functions to alternative bases. Trans. Amer. Math. Soc. To appear.Google Scholar
4.Berndt, B. C., Chan, H. H. and Zhang, L. C.. Ramanujan's class invariants and cubic continued fraction. Ada Arith. To appear.Google Scholar
5.Borwein, J. M. and Borwein, P. B.. Pi and the AGM (Wiley, New York, 1987).Google Scholar
6.Borwein, J. M. and Borwein, P. B.. A cubic counterpart to Jacobi's identity and the AGM. Trans. Amer. Math. Soc, 323 (1991), 691–701.Google Scholar
7.Borwein, J. M. and Zucker, I. J.. Fast evaluation of the gamma function for small rational fractions using complete elliptic integrals of the first kind. IMA J. Numerical Anal., 12 (1992), 519–526.CrossRefGoogle Scholar
8.Cox, D. A.. Primes of the form x2 + ny2 (Wiley, New York, 1989).Google Scholar
9.Hall, H. S. and Knight, S. R.. Higher Algebra (Macmillan, London, 1957).Google Scholar
10.Huard, J. G., Kaplan, P. and Williams, K. S.. The Chowla-Selberg formula for genera. Ada Arith. To appear.Google Scholar
11.Joyce, G. S. and Zucker, I. J.. Special values of the hypergeometric series. Math. Proc. Cambridge Phil. Soc, 109 (1991), 257–261.Google Scholar
12.Kaplan, P. and Williams, K. S.. The Chowla-Selberg formula for non-fundamental discriminants. To appear.Google Scholar
13.Landau, S.. How to tangle with a nested radical. Math. Intell, 16 (1994), 49–55.Google Scholar
14.Ramanujan, S.. Modular equations and approximations to Π. Quart. J. Math. (Oxford), 45 (1914), 350–372.Google Scholar
15.Ramanujan, S.. Notebooks (2 volumes) (Tata Institute of Fundamental Research, Bombay, 1957).Google Scholar
16.Ramanujan, S.. Collected Papers (Chelsea, New York, 1962).Google Scholar
17.Watson, G. N.. Some singular moduli (II). Quart. J. Math., 3 (1932), 189–212.CrossRefGoogle Scholar
18.Watson, G. N.. Singular moduli (5). Proc. London Math. Soc, 42 (1937), 377–397.CrossRefGoogle Scholar
19.Weber, H.. Lehrbuch der Algebra, dritter Band (Chelsea, New York, 1961).Google Scholar
20.Whittaker, E. T. and Watson, G. N.. A Course of Modern Analysis, 4th ed. (Cambridge University Press, Cambridge, 1966).Google Scholar
21.Williams, K. S. and Nan-Yue, Zhang. The Chowla-Selberg relation for genera. To appear.Google Scholar
22.Zippel, R.. Simplification of expressions involving radicals. J. Symbolic Comp., 1 (1985), 189–210.Google Scholar
23.Zucker, I. J.. The evaluation in terms of Г-functions of the periods of elliptic curves admitting complex multiplication. Math. Proc. Cambridge Phil. Soc, 82 (1977), 111–118.CrossRefGoogle Scholar