No CrossRef data available.
Article contents
Reconstructing curves from sets of quantized observations
Published online by Cambridge University Press: 26 February 2010
Extract
For arbitrary f: R → R and ϒ ⊂ Z × R we define the set 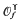 of quantized observations of f relative to ϒ as follows: for each integer n and each y∈R we write
of quantized observations of f relative to ϒ as follows: for each integer n and each y∈R we write
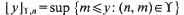
(the supremum of an empty set is taken to be −∞ ) and we put
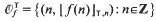
Thus for example 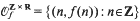 and
and 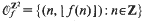 , where [x] (without subscript) denotes as usual the integer part of x.
, where [x] (without subscript) denotes as usual the integer part of x.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1995
References
1.Bruijn, N. G. de. Updown generation of Beatty sequences. Proc. Kon. Ned. Akad. Wet., A, 92 (1989), 385–407.Google Scholar
2.Corput, J. G. van der. Über Gitterpunkte in der Ebene. Math. Ann., 81 (1920), 1–20.CrossRefGoogle Scholar
3.Graham, S. W. and Kolesnik, G.. Van der Corpufs method for exponential sums. LMS Lecture Notes, 115 (Cambridge University Press, 1987).Google Scholar
5.Jarnik, V., Über die Gitterpunkte auf konvexen Kurven. Math. Zeit., 24 (1925), 500–518.CrossRefGoogle Scholar
6.Kendall, D. G.. On the number of lattice points inside a random oval. Quart. J. Math. (Oxford series), 19 (1948), 1–26.CrossRefGoogle Scholar
7.Rooij, A. C. M. van and Schikhof, W. H.. A second course on real functions (Cambridge University Press, 1982).CrossRefGoogle Scholar
8.Vershik, A. M.. The limit shape theorem for convex lattice polygons and related topics. Fund. Anal. Appl. To appear.Google Scholar

