No CrossRef data available.
Article contents
Riemann equivalence of functions
Published online by Cambridge University Press: 26 February 2010
Extract
Two finite real functions ƒ(x) and g(x), defined for — ∞ < x < ∞, are said to be Riemann equivalent if |ƒ(x)—g(x)| has a zero Riemann integral over every finite interval; we then write ƒ~g or
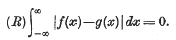
N. G. de Bruijn conjectured that if ƒ(x+h)~ƒ(x) for every real number h, then ƒ~c where c is a constant; this was proved by P. Erdös [1]. In this note we associate with an arbitrary function ƒ the additive group 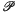 (ƒ) of all numbers h which make ƒ(x)~ƒ(x+h), i.e. which make
(ƒ) of all numbers h which make ƒ(x)~ƒ(x+h), i.e. which make
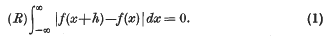
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1955
References
1.Erdös, P., “A theorem on the Riemann integral”, Indag. Math., 14, No. 2 (1952), 142–144.CrossRefGoogle Scholar
2.Souslin, M., “Sur un corps non-dénombrable de nombres réels”, Fundamenta Math., 4 (1923), 311–315.CrossRefGoogle Scholar
3.Sierpiński, W., “… la Base de M. Hamel”, Fundamenta Math., 1 (1920), 105–111.CrossRefGoogle Scholar

