Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T23:01:41.105Z Has data issue: false hasContentIssue false
  • English
  • Français

Separation of K–analytic sets

Part of: Connections with other structures, applications

Published online by Cambridge University Press:  26 February 2010

R. W. Hansell ,
J. E. Jayne  and
C. A. Rogers
R. W. Hansell
Affiliation:
Department of Mathematics, University of Connecticut, Storrs, Connecticut 06268, U.S.A..
J. E. Jayne
Affiliation:
Department of Mathematics, University College London, Gower Street, London, WC1E 6BT
C. A. Rogers
Affiliation:
Department of Mathematics, University College London, Gower Street, London, WC1E 6BT
Get access

Extract

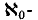In [5] we have developed part of a theory of K- analytic sets that forms a common generalization of the theory of Lindelöf K- analytic sets developed by Choquet, Sion and Frolik and the theory of metric analytic sets developed by Stone and Hansell. As we explain in [5], this theory parallels the recently developed theory of Frolík and Holický, but has certain advantages. In this paper we take the theory rather further, and, in particular, we prove a number of variants of Lusin's first separation theorem and give some of their applications. We make free use of the definitions, notation and conventions introduced in [5].

MSC classification

Secondary: 54H05: Descriptive set theory (topological aspects of Borel, analytic, projective, etc. sets)
Type
Research Article
Information
Mathematika , Volume 32 , Issue 1 , June 1985 , pp. 147 - 190
Copyright
Copyright © University College London 1985

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Davies, R. O., Jayne, J. E., Ostaszewski, A. J. and Rogers, C. A.. Theorems of Novikov type. Mathemalika, 24 (1977), 97–114.Google Scholar
2.Engelking, R.. General Topology (PWN, Warsaw, 1977).Google Scholar
3.Frohík, Z.. Lusin sets are additive. Comment. Math. Univ. Carotin., 21 (1980), 527–533.Google Scholar
4.Hansell, R. W.. On the representation of nonseparable analytic sets. Proc. Amer. Math. Soc, 39 (1973), 402–408.CrossRefGoogle Scholar
5.Hansell, R. W., Jayne, J. E. and Rogers, C. A., K-analytic sets. Mathematika, 30 (1983), 189–221.Google Scholar
6.Hansell, R. W., Jayne, J. E. and Rogers, C. A.. K-analytic sets: corrigenda et addenda. Mathematika, 31 (1984), 28–32.CrossRefGoogle Scholar
7.Jayne, J. E.. Generation of σ-algebras, Baire sets and descriptive Borel sets. Mathematika, 24 (1977), 241–256.CrossRefGoogle Scholar
8.Novikov, P. S.. Sur la séparabilite-B dénombrable des ensembles analytiques. Dokl. Akad. Nauk SSSR, 3 (1934), 145–148.Google Scholar
9.Novikov, P. S.. On the projection of certain B-sets. Dokl. Akad. Nauk SSSR, 23 (1939), 863–864.Google Scholar
10.Rogers, C. A., Jayne, J. E., Dellacherie, C., Topsøe, F., Hoffmann-Jørgensen, J., Martin, D. A., Kechris, A. S. and Stone, A. H.. Analytic Sets (Academic Press, London, 1980).Google Scholar
11.Sierpiński, W.. Funkeje Przedstawialne Analityncznie, in Polish (Lwow, 1925).Google Scholar