Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-29T02:23:59.087Z Has data issue: false hasContentIssue false
  • English
  • Français

Short surface waves due to an oscillating half-immersed sphere

Part of: Incompressible inviscid fluids

Published online by Cambridge University Press:  26 February 2010

A. M. J. Davis
A. M. J. Davis
Affiliation:
Department of Mathematics, University College, London.
Get access

Extract

This paper uses systems of image sources to construct suitable generalised Green's functions for considering small amplitude short surface waves due to an oscillating immersed sphere. A sphere of radius a is half-immersed in a fluid under gravity and is making vertical oscillations of small constant amplitude and period 2π/σ about this position. It is required to find the fluid motion, and in particular the virtual mass and wavemaking coefficients. For sufficiently small amplitudes the motion depends non-trivially on only a single dimensionless parameter

where g is the gravitational acceleration. This was shown by Ursell in an unpublished U. S. Navy report in which the methods of an earlier paper (Ursell, 1949) were adapted from cylindrical to spherical symmetry and resolved the conflict between Havelock (1955) and Barakat (1962) in favour of the former. Ursell showed that the virtual mass coefficient is

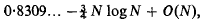
i.e. infinitely increasing initially so that Barakat's results must be incorrect near N = 0. However, although existence is proved for all N, the same difficulty arises as with the heaving cylinder, namely computation is only practical for values of N up to about 1. In the cylindrical case, Ursell (1953) developed a method for finding the asymptotic solution for large N and here it will be adapted, surprisingly perhaps, to deal with the spherical case. Ursell (1954) then published a formal solution which gave the same virtual mass as the rigorous treatment and if this formal method is applied to the heaving sphere, the virtual mass coefficient obtained is

MSC classification

Secondary: 76B15: Water waves, gravity waves; dispersion and scattering, nonlinear interaction
Type
Research Article
Information
Mathematika , Volume 18 , Issue 1 , June 1971 , pp. 20 - 39
Copyright
Copyright © University College London 1971

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barakat, R., 1962, J. Fluid Mech, 13, 540–556.Google Scholar
Copson, E. T., 1965, Asymptotic Expansions (Cambridge University Press).Google Scholar
Davis, A. M. J., 1965, Proc. Camb. Phil. Soc, 61, 827–846.CrossRefGoogle Scholar
Havelock, T., 1955, Proc. Roy. Soc. London A, 231, 1–7.Google Scholar
Holford, R. L., 1965, Technical Report, Department of Mathematics, Stanford University.Google Scholar
John, F., 1950, Commun. Pure Appl. Math., 3, 45–101.Google Scholar
Lamb, H., 1932, Hydrodynamics, 6th edition (Cambridge University Press).Google Scholar
Rhodes-Robinson, P. F., 1970, Proc. Camb. Phil. Soc, 67, 423–442, 443-468.Google Scholar
Ursell, F., 1949, Quart. J. Mech. Appl. Math., 2, 218–231.Google Scholar
Ursell, F. 1953, Proc. Roy. Soc. London A, 220, 90–103.Google Scholar
Ursell, F. 1954, Quart. J. Mech. Appl. Math., 7, 427–437.CrossRefGoogle Scholar
Ursell, F. 1957, Proc. Symp. Behaviour of Ships in a Seaway (Wageningen).Google Scholar
Ursell, F. 1961, Proc. Camb. Phil. Soc, 57, 638–668.CrossRefGoogle Scholar
Watson, G. N., 1944, Theory of Bessel Functions 2nd edition (Cambridge University Press).Google Scholar