Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T21:01:56.341Z Has data issue: false hasContentIssue false
  • English
  • Français

SHUTOUT GAMES ON GRAPHS

Part of: Graph theory Game theory

Published online by Cambridge University Press:  03 February 2015

Alexandru Cioba  and
Michail Savvas
Alexandru Cioba
Affiliation:
Department of Mathematics, University College London, 25 Gordon Street, London WC1H 0AY, U.K. email a.cioba.12@ucl.ac.uk
Michail Savvas
Affiliation:
Department of Mathematics, Stanford University, 450 Serra Mall, Building 380, Stanford 94305-2125, U.S.A. email msavvas@math.stanford.edu
Get access

Abstract

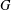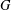Two players take it in turn to claim edges from a graph $G$. The first player (“Maker”) wins if at any point he has claimed $s$ edges at a vertex without the second player (“Breaker”) having claimed a single edge at that vertex. If, by the end of play, this does not occur we say that Breaker wins. Our main aim is to show that for every $s$ there is a graph $G$ in which Maker has a winning strategy.

MSC classification

Primary: 91A43: Games involving graphs 91A46: Combinatorial games 05C57: Games on graphs
Type
Research Article
Information
Mathematika , Volume 61 , Issue 3 , September 2015 , pp. 523 - 530
Copyright
Copyright © University College London 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Beck, J., Combinatorial Games: Tic-Tac-Toe Theory (Encyclopedia of Mathematics and Its Applications 114), Cambridge University Press (Cambridge, 2008).CrossRefGoogle Scholar
Leader, I., Hypergraph Games. Notes available online at http://tartarus.org/gareth/maths/notes/.Google Scholar