Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T21:55:27.302Z Has data issue: false hasContentIssue false
  • English
  • Français

Small positive values of indefinite ternary forms

Part of: Geometry of numbers

Published online by Cambridge University Press:  26 February 2010

Terence Jackson
Terence Jackson
Affiliation:
Mathematics Department, University of York, Heslington, York YO10 5DD, England.
Get access

Abstract

For an indefinite quadratic form f(x1,…,xn) of discriminant d. let P(f) denote the greatest lower bound of the positive values assumed by f for integers x1, …, xn. This paper investigates the values of P3/|d| for nonzero ternary forms of signature −1, and finds the only remaining class of forms with .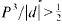

MSC classification

Secondary: 11H50: Minima of forms
Type
Research Article
Information
Mathematika , Volume 49 , Issue 1-2 , June 2002 , pp. 185 - 196
Copyright
Copyright © University College London 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Dani, S. G. and Margulis, G. A.. Values of quadratic forms at integral points: an elementary approach. Enseign. Math. (2), 36 (1990), 143–174.Google Scholar
2.Jackson, T. H.. One-sided inequalities for ternary forms I. J. Number Theory, 13 (1981), 376–397.Google Scholar
3.Jackson, T. H.. One-sided inequalities for ternary forms II. J. Number Theory. 16 (1983). 333–342.CrossRefGoogle Scholar
4.Mahler, K.. A theorem of B. Segre. Duke Math. J., 12 (1945), 367–371.CrossRefGoogle Scholar
5.Segre, B.. Lattice points in infinite domains and asymmetric Diophantine approximations. Duke-Math. J., 12 (1945), 337–365.CrossRefGoogle Scholar
6.Watson, G. L.. Integral quadratic forms, Cambridge University Press, Cambridge (1960).Google Scholar
7.Worley, R. T.. Non-negative values of quadratic forms. J. Austral. Math. Soc., 12 (1971). 224–238.CrossRefGoogle Scholar