Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-11T05:57:23.426Z Has data issue: false hasContentIssue false
  • English
  • Français

Small solutions of quadratic and quartic congruences

Published online by Cambridge University Press:  26 February 2010

R. C. Baker
R. C. Baker
Affiliation:
Royal Holloway College, Egham, Surrey
Get access

Extract

The present investigation was suggested by a theorem of A. Schinzel, H. P. Schlickewei and W. M. Schmidt [6]: let Q(x) = Q(x1,…, xs) be a quadratic form with integer coefficients. Then for each natural number m there are integers x1,…, xs satisfying

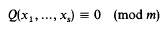
and having

Type
Research Article
Information
Mathematika , Volume 27 , Issue 1 , June 1980 , pp. 30 - 45
Copyright
Copyright © University College London 1980

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Baker, R. C. and Schmidt, W. M.. “Diophantine problems with variables restricted to 0 and 1”, J. Number Theory (to appear).Google Scholar
2.Birch, B. J.. “Homogeneous forms of odd degree in a large number of variables”, Mathematika, 4 (1957), 102–105.CrossRefGoogle Scholar
3.Borevich, Z. I. and Shafarevich, I. R.. Number Theory (Academic Press, New York, 1966).Google Scholar
4.Cassels, J. W. S.. “Bounds for the least solutions of homogeneous quadratic equations”, Proc. Cambridge Philos. Soc, 51 (1955), 262–264.CrossRefGoogle Scholar
5.Cassels, J. W. S.. An introduction to Diophantine approximation (Cambridge University Press, London, 1957).Google Scholar
6.Schinzel, A., Schlickewei, H. P. and Schmidt, W. M.. “Small solutions of quadratic congruences and small fractional parts of quadratic forms”, Acta Arith. (to appear).Google Scholar
7.Schmidt, W. M.. “Small zeros of additive forms in many variables”, Trans. Amer. Math. Soc, 248 (1979), 121–133.CrossRefGoogle Scholar
8.Schmidt, W. M.. “Diophantine inequalities for forms of odd degree”, Advances in Math, (to appear).Google Scholar