Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Chernyavskaya, Nina A.
and
Shuster, Leonid A.
2014.
Methods of analysis of the condition for correct solvability in L p (ℝ) of general Sturm-Liouville equations.
Czechoslovak Mathematical Journal,
Vol. 64,
Issue. 4,
p.
1067.
Chernyavskaya, N.
and
Shuster, L.
2025.
Necessary and sufficient conditions for the solvability of a singular Dirichlet boundary problem for the Sturm-Liouville equation of general form.
Journal of Differential Equations,
Vol. 416,
Issue. ,
p.
1564.

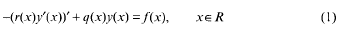
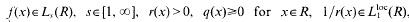 ,
, 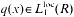 . The inversion problem for (1) is called regular in
. The inversion problem for (1) is called regular in 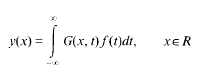
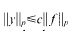 . Here
. Here 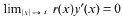 for any
for any 