Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Shirasaka, S.
2002.
On the Laurent coefficients of a class of Dirichlet series.
Results in Mathematics,
Vol. 42,
Issue. 1-2,
p.
128.
Ding, Liping
Li, Hailong
and
Shirasaka, S.
2005.
Abelian and Tauberian results on Dirichlet series.
Results in Mathematics,
Vol. 48,
Issue. 1-2,
p.
27.
BANERJEE, D.
CHAKRABORTY, K.
KANEMITSU, S.
and
MAJI, B.
2017.
ABEL-TAUBER PROCESS AND ASYMPTOTIC FORMULAS.
Kyushu Journal of Mathematics,
Vol. 71,
Issue. 2,
p.
363.
Wang, N.-L.
Agarwal, Praveen
and
Kanemitsu, S.
2020.
Limiting Values and Functional and Difference Equations.
Mathematics,
Vol. 8,
Issue. 3,
p.
407.

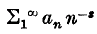 and if
and if 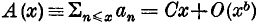 where 0 ≤
where 0 ≤