Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Semple, J. G.
and
Tyrrell, J. A.
1969.
The Cremona transformation of
S
6
by quadrics through a normal elliptic septimic scroll
1
R
7
.
Mathematika,
Vol. 16,
Issue. 1,
p.
88.
Dolgachev, I. V.
and
Iskovskikh, V. A.
1976.
Geometry of algebraic varieties.
Journal of Soviet Mathematics,
Vol. 5,
Issue. 6,
p.
803.
Pan, Ivan
and
Russo, Francesco
2005.
Cremona transformations and special double structures.
manuscripta mathematica,
Vol. 117,
Issue. 4,
p.
491.
Gonzalez-Sprinberg, Gerard
and
Pan, Ivan
2006.
On Characteristic Classes of Determinantal Cremona Transformations.
Mathematische Annalen,
Vol. 335,
Issue. 2,
p.
479.
Costa, Barbara
Simis, Aron
and
Ramos, Zaqueu
2014.
A theorem about Cremona maps and symbolic Rees algebras.
International Journal of Algebra and Computation,
Vol. 24,
Issue. 08,
p.
1191.
Alzati, Alberto
and
Sierra, José Carlos
2016.
Special birational transformations of projective spaces.
Advances in Mathematics,
Vol. 289,
Issue. ,
p.
567.
Mostafazadehfard, Maral
and
Simis, Aron
2016.
Homaloidal determinants.
Journal of Algebra,
Vol. 450,
Issue. ,
p.
59.
Staglianò, Giovanni
2020.
Special cubic birational transformations of projective spaces.
Collectanea Mathematica,
Vol. 71,
Issue. 1,
p.
123.
Ramos, Zaqueu
and
Simis, Aron
2024.
Determinantal Ideals of Square Linear Matrices.
p.
201.

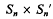 of two
of two 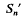 (regarded as an irreducible algebraic system of ∞
(regarded as an irreducible algebraic system of ∞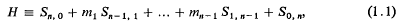
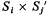 of
of