Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kundu, Debanjana
and
Washington, Lawrence C.
2024.
Heuristics for Anti-cyclotomic ℤ
p
-extensions
.
Experimental Mathematics,
Vol. 33,
Issue. 4,
p.
644.
Itoh, Tsuyoshi
2025.
Class number behavior in a two-tiered tower of ℤp-extensions.
International Journal of Number Theory,
Vol. 21,
Issue. 07,
p.
1547.
Gras, Georges
2026.
Initial layer of the anti-cyclotomic Zp-extension of Q(−m) and capitulation phenomenon.
Journal of Number Theory,
Vol. 280,
Issue. ,
p.
634.

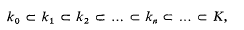
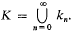 Let
Let 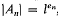 , with
, with
