Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T23:21:13.053Z Has data issue: false hasContentIssue false
  • English
  • Français

Subsets of positive finite measure in the space of compact subsets of the unit interval

Part of: Classical measure theory

Published online by Cambridge University Press:  26 February 2010

P. R. Goodey
P. R. Goodey
Affiliation:
Department of Mathematics, Royal Holloway College, Englefield Green, Surrey.
Get access

Extract

Definitions. We say that h is a Hausdorff measure function if it satisfies the following conditions:

(i) 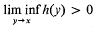for all x > 0,

(ii) h(x) → 0 as x → 0,

(iii) h(x) is monotonic increasing.

MSC classification

Secondary: 28A75: Length, area, volume, other geometric measure theory
Type
Research Article
Information
Mathematika , Volume 21 , Issue 2 , December 1974 , pp. 189 - 192
Copyright
Copyright © University College London 1974

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Boardman, E., “Some Hausdorff measure properties of the space of compact subsets of (0, 1)”, Quart. J. Math. Oxford (2), 24 (1973), 333–341.CrossRefGoogle Scholar
2.Goodey, P. R.. “On Hausdorff measure in Hilbert space”, Quart. J. Math. Oxford (2), 22 (1971), 271–276.Google Scholar
3.Goodey, P. R.. “On Hausdorff measure in Hilbert space (II)”, Quart J. Math. Oxford (2), 24 (1973), 107–117.CrossRefGoogle Scholar
4.Kuratowski, C.. Topologie, Volume 2 (Warszawa, 1952).Google Scholar