Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Pratt, Philip
1972.
Representation theorems for functions holomorphic and meromorphic in the unit disk.
Mathematische Zeitschrift,
Vol. 125,
Issue. 2,
p.
101.
1989.
Subharmonic Functions.
p.
865.

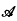 be the class of non-constant functions
be the class of non-constant functions 