Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T21:57:28.146Z Has data issue: false hasContentIssue false
  • English
  • Français

THE TILED CIRCLE PROBLEM

Part of: Additive number theory; partitions Discrete geometry

Published online by Cambridge University Press:  31 March 2014

M. N. Huxley
M. N. Huxley*
Affiliation:
School of Mathematics, University of Cardiff, 23 Senghennydd Road, Cardiff CF24 4AG, U.K. email huxley@cardiff.ac.uk
Get access

Abstract

How many square tiles are needed to tile a circular floor? Tiles are cut to fit the boundary. We give an algorithm for cutting, rotating and re-using the off-cut parts, so that a circular floor requires 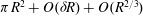$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}} \pi R^2 + O(\delta R) + O(R^{2/3}) $ tiles, where 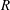$R$ is the radius and 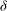$\delta $ is the width of the cutting tool. The algorithm applies to any oval-shaped floor whose boundary has a continuous non-zero radius of curvature. The proof of the error estimate requires methods of analytic number theory.

MSC classification

Secondary: 11P21: Lattice points in specified regions 52C05: Lattices and convex bodies in $2$ dimensions
Type
Research Article
Information
Mathematika , Volume 60 , Issue 2 , July 2014 , pp. 321 - 346
Copyright
Copyright © University College London 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bombieri, E. and Iwaniec, H., On the order of ζ (1∕2 + i t). Ann. Sc. Norm. Super. Pisa Cl. Sci. (4) 13 1986, 449–472.Google Scholar
Corput, J. G. v. d., Over Roosterpunten in het Platte Vlak, Noordhof (Groningen, 1919).Google Scholar
Corput, J. G. v. d., Beweis einer approximativen Funktionalgleichung. Math. Z. 28 1928, 238–310.CrossRefGoogle Scholar
Corput, J. G. v. d., Neue zahlentheoretische Abschätzungen. Math. Z. 29 1928/29, 397–426.Google Scholar
Francesca, P. d., De prospectiva pingendi, Heitz (1897).Google Scholar
Francesca, P. d., Il battesimo, Wikimedia Commons file, http://commons.wikimedia.org/wiki/File:Piero,_battesimo,_schema.jpg.Google Scholar
Graham, S. W. and Kolesnik, G., Van der Corput’s Method of Exponential Sums (London Mathematical Society Lecture Notes 126), Cambridge University Press (1991).Google Scholar
Huxley, M. N., On the differences of primes in arithmetic progressions. Acta Arithmetica 15 1969, 364–388.CrossRefGoogle Scholar
Huxley, M. N., Area, Lattice Points, and Exponential Sums (London Mathematical Society Monographs 13), Oxford University Press (1996).CrossRefGoogle Scholar
Huxley, M. N., Exponential sums and lattice points III. Proc. Lond. Math. Soc. (3) 87 2003, 591–609.Google Scholar
Iwaniec, H. and Mozzochi, C. J., On the divisor and circle problems. J. Number Theory 29 1988, 60–93.Google Scholar
Jarník, V., Über die Gitterpunkte auf konvexen Kurven. Math. Zeitschrift 24 1925, 500–518.Google Scholar
Karatsuba, A. A., On the distance between consecutive zeros of the Riemann zeta-function on the critical line. Tr. Mat. Inst. Steklova A.N.S.S.R. 157 1981, 49–63.Google Scholar
Kendall, D. G., On the number of lattice points inside a random oval. Q. J. Math. 19 1948, 1–26.Google Scholar
Phillips, E., The zeta-function of Riemann: further developments of van der Corput’s method. Q. J. Math. 4 1933, 209–225.Google Scholar
Sierpiński, W., O pewnem zagadneniu w rachunku funkcyj asymptoticznych. Prace Mat.-Fiz 17 1906, 77–118.Google Scholar
Voronoï, G., Sur un problème du calcul des fonctions asymptotiques. J. Reine Angew. Math 126 1903, 241–282.Google Scholar