Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-13T10:38:06.975Z Has data issue: false hasContentIssue false
  • English
  • Français

T-invariant algebras on Riemann surfaces

Part of: Riemann surfaces

Published online by Cambridge University Press:  26 February 2010

André Boivin
André Boivin
Affiliation:
Department of Mathematics, The University of Western Ontario, London, Ontario, Canada, N6A 5B7.
Get access

Abstract

The main purpose of this article is to outline for non-compact Riemann surfaces the development of a theory of T-invariant algebras similar to that developed by T. W. Gamelin [7] in the case of the plane. The main idea is to introduce, using the global local uniformizer of R. C. Gunning and R. Narashimhan, a Cauchy transform operator for the Riemann surface which operates on measures and solves an inhomogeneous 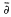-equation. This, in turn, can be used, analogously to the Cauchy transform on the plane, to develop meromorphic (rational) approximation theory. We sketch the path of the development but omit most of the details when they are very much similar to the planar case. Our presentation follows closely that of [7]. The original motivation for this study was to obtain more information on Gleason parts useful in the study of Carleman (tangential) approximation theory (see [5]).

MSC classification

Secondary: 30F99: None of the above, but in this section
Type
Research Article
Information
Mathematika , Volume 34 , Issue 2 , December 1987 , pp. 160 - 171
Copyright
Copyright © University College London 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Arens, R.. The closed maximal ideals of algebras of functions holomorphic on a Riemann surface. Rend. Circ. Mat. Palermo (2), 7 (1958), 245–260.CrossRefGoogle Scholar
2.Behnke, H.H., and Stein, K.. Entwicklung analytischer Funktionen auf Riemannschen Flächen. Math. Ann., 120 (1949), 430–461.CrossRefGoogle Scholar
3.Bishop, E.. A minimal boundary for function algebras. Pacific J. Math., 9 (1959), 629–642.CrossRefGoogle Scholar
4.Boivin, A.. Algèbres T-invariahts sur les surfaces de Riemann non compactes. Université de Montréal, Dept. of Math. Report No. 1986-22.Google Scholar
5.Boivin, A.. Carleman approximation on Riemann surfaces. Math. Ann. 275 (1986), 57–70.CrossRefGoogle Scholar
6.Gamelin, T. W.. Uniform Algebras, Second Edition (Chelsea, 1984).Google Scholar
7.Gamelin, T. W.. Rational Approximation Theory, University of California, Los Angeles, Course Notes for Math 285G, Fall 1975.Google Scholar
8.Gamelin, T. W. and Lumer, G.. Theory of abstract Hardy spaces and the Universal Hardy class. Adv. in Math., 2 (1968), 118–174.CrossRefGoogle Scholar
9.Gauthier, P. M.. Meromorphic uniform approximation on closed subsets of open Riemann surfaces. Approximation Theory and Functional Analysis, Proc. Conf. Campinas 1977, Prolla, J. B. ed. (North-Holland, 1979), 139–158.Google Scholar
10.Gunning, R. C. and Narasimhan, R.. Immersion of open Riemann surfaces. Math. Ann., 174 (1967), 103–108.CrossRefGoogle Scholar
11.Rossi, H.. Algebras of holomorphic functions on one-dimensional varieties. Trans., Amer. Math. Soc., 100 (1961), 439–458.CrossRefGoogle Scholar
12.Scheinberg, S.. Uniform approximation by functions analytic on a Riemann surface. Ann. of Math. (2), 108 (1978), 257–298.CrossRefGoogle Scholar
13.Wilken, D.. The support of representing measures for R(X). Pacific J. Math., 26 (1968), 621–626.CrossRefGoogle Scholar