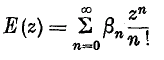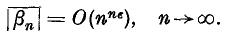Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Shidlovskii, A. B.
1967.
Transcendence measure estimates for the values of E-functions.
Mathematical Notes of the Academy of Sciences of the USSR,
Vol. 2,
Issue. 1,
p.
508.
Galochkin, A. I.
1968.
Estimate of the conjugate transcendence measure for the values of E-functions.
Mathematical Notes of the Academy of Sciences of the USSR,
Vol. 3,
Issue. 4,
p.
240.
Shidlovsky, A. B.
1983.
Studies in Pure Mathematics.
p.
635.
Chudnovsky, D. V.
and
Chudnovsky, G. V.
1984.
Number Theory.
Vol. 1052,
Issue. ,
p.
85.
Brownawell, W. Dale
1985.
Effectivity in independence measures for values ofE-functions.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 39,
Issue. 2,
p.
227.
Dvornicich, Roberto
and
Traverso, Carlo
1989.
Applied Algebra, Algebraic Algorithms and Error-Correcting Codes.
Vol. 356,
Issue. ,
p.
216.
Hazewinkel, M.
1992.
Encyclopaedia of Mathematics.
p.
197.
Lang, Serge
2000.
Collected Papers.
p.
396.
Bertrand, Daniel
2012.
Number Theory, Analysis and Geometry.
p.
51.
Narkiewicz, Władysław
2012.
Rational Number Theory in the 20th Century.
p.
131.
Chirskii, V. G.
2017.
Topical problems of the theory of Transcendental numbers: Development of approaches to their solution in the works of Yu. V. Nesterenko.
Russian Journal of Mathematical Physics,
Vol. 24,
Issue. 2,
p.
153.