Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Yu, Jing
1985.
Transcendence theory over function fields.
Duke Mathematical Journal,
Vol. 52,
Issue. 2,
Yu, Jing
1986.
Transcendence and Drinfeld modules.
Inventiones Mathematicae,
Vol. 83,
Issue. 3,
p.
507.
Yu, Jing
1992.
The Arithmetic of Function Fields.
p.
253.

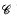 be a smooth projective, geometrically irreducible curve over a finite field
be a smooth projective, geometrically irreducible curve over a finite field 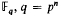 . We fix a rational point ∞on
. We fix a rational point ∞on 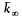 whose elements will be called “numbers”.
whose elements will be called “numbers”.