Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T22:31:24.551Z Has data issue: false hasContentIssue false
  • English
  • Français

Trapped modes in a waveguide with a thick obstacle

Part of: Spectral theory and eigenvalue problems

Published online by Cambridge University Press:  26 February 2010

Helen Hawkins  and
Leonid Parnovski
Helen Hawkins
Affiliation:
Centre for Mathematical Analysis and Its Applications, University of Sussex, Falmer, Brighton BN1 9QH, UK. E-mail: h.l.hawkins@sussex.ac.uk
Leonid Parnovski
Affiliation:
Department of Mathematics, University of College London, Gower Street, London WC1E 6BT, UK. E-mail: Leonid@math.ucl.ac.uk.
Get access

Extract

The problem of finding necessary and sufficient condi-tions for the existence of trapped modes in waveguides has been known since 1943. [10]. The problem is the following: consider an infinite strip M in ℝ2(or an infinite cylinder with the smooth boundary in ℝn). The spectrum of the(positive) Laplacian, with either Dirichlet or Neumann boundary conditions, acting on this strip is easily computable via the separation of variables; the spectrum is absolutely continuous and equals [v0,+∞). Here, v0 is the first threshold, i.e., eigenvalue of the cross-section of the cylinder (so v0 = 0 in the case of Neumann conditions). Let us now consider the domain 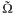(the waveguide) which is a smooth compact perturbation of M (for example, weinsert an obstacle inside M). The essential spectrum of the Laplacian acting on 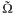still equals [v0, +ℝ), but there may be additional eigenvalues, which are often called trapped modes; the number of these trapped modes can be quite large, see examples in [11] and [8].

MSC classification

Secondary: 35P15: Estimation of eigenvalues, upper and lower bounds
Type
Research Article
Information
Mathematika , Volume 51 , Issue 1-2 , December 2004 , pp. 171 - 186
Copyright
Copyright © University College London 2004

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Adams, R. A., Sobolev spaces. Academic Press, (1975).Google Scholar
2.Borisov, D., Exner, P. and Gadyl'shin, R., Geometric coupling thresholds in a two-dimensionalstrip. J. Math. Phys., 43 (2002), 6265–6278.CrossRefGoogle Scholar
3.Davies, E. B. and Parnovski, L., Trapped modes in acoustic waveguides. Q. J. Mech. and Appl. Maths., 51 (1998), 477–192.CrossRefGoogle Scholar
4.Evans, D. V., Levitin, M. and Vassiliev, D., Existence theorems for trapped modes. J Fluid Mech., 261 (1994), 21–31.CrossRefGoogle Scholar
5.Exner, P., Laterally coupled quantum waveguides. Cont. Math., 217 (1998). 6982.CrossRefGoogle Scholar
6.Exner, P. and Vugalter, S. A., Asymptotic estimates for bound states in quantum waveguides coupled laterally through a narrow window. Ann. Inst. Henri Poincare. Phys. Theor.. 65 (1) (1996), 109–123.Google Scholar
7.Khallaf, N. S. A., Parnovski, L. and Vassiliev, D., Trapped modes in a waveguide with a long obstacle. J. Fluid Mech., 403 (2000), 251–261.CrossRefGoogle Scholar
8.Parnovski, L., Spectral asymptotics of the Laplace operator on manifolds with cylindrical ends. Int. J. Math., 6 (1995), 911–920.CrossRefGoogle Scholar
9.Popov, Y., Asymptotics of bound states for laterally coupled waveguides. Rep. op. Math. Phys., 43 (3) (1999), 427–437.CrossRefGoogle Scholar
10.Rellich, F., Uber das asymptotische Verhalten der Losungen von D + lu = 0 in unendlichen Gebieten. Jahresberichte Deutsch. Math.-Verein, 53 (1943), 57–65.Google Scholar
11.Witsch, K. J., Examples of embedded eigenvalues for the Dirichlet-Laplacian in domains with infinite boundaries. Math. Met. Appl. Sc., 12 (1990), 177–182.CrossRefGoogle Scholar