Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T22:48:07.873Z Has data issue: false hasContentIssue false
  • English
  • Français

Universal graphs without large bipartite subgraphs

Published online by Cambridge University Press:  26 February 2010

Péter Komjáth  and
János Pach
Péter Komjáth
Affiliation:
Mathematical Institute, Hungarian Academy of Sciences, Budapest, V. Reáltanoda u. 13–15, Hungary.
János Pach
Affiliation:
Mathematical Institute, Hungarian Academy of Sciences, Budapest, V. Reáltanoda u. 13–15, Hungary.
Get access

Abstract

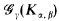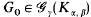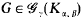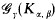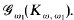Let 1 ≤ α ≤ β ≤ γ be cardinals, and let denote the class of all graphs on γ vertices having no subgraph isomorphic to Kα,β. A graph is called universal if every can be embedded into Go as a subgraph. We prove that, if α < ω ≤ γ and the General Continuum Hypothesis is assumed, then has a universal element, if, and only if, (i) γ > ω or (ii) γ = ω, α = 1 and β ≤ 3. Using the Axiom of Constructibility, we also show that there does not exist a universal graph in .

Type
Research Article
Information
Mathematika , Volume 31 , Issue 2 , December 1984 , pp. 282 - 290
Copyright
Copyright © University College London 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Chang, C. C. and Kiesler, H. J.. Model theory (North-Holland, Amsterdam, London, New York, 1973).Google Scholar
2.Devlin, K. J.. The axiom ofconstructibility, A guide for the mathematician, Lecture Notes in Mathematics, 617 (Springer, Berlin-Heidelberg-New York, 1977).Google Scholar
3.Erdos, P. and Spencer, J.. Probabilistic methods in combinatorics (Academic Press, New York-London, 1974).Google Scholar
4.Hajnal, A. and Mété, A.. Set mappings, partitions, and chromatic numbers, Logic Colloquium '73 (Bristol). Studies in Logic and the Foundations of Mathematics, 80 (North-Holland, Amsterdam, 1975), 347–379.Google Scholar
5.Hajnal, A. and Pach, J.. Monochromatic paths in infinite graphs. In Finite and Infinite Sets. Coll. Math. Soc. J. Bolyai, 37 (Eger, 1981), 359–369.Google Scholar
6.Rado, R.. Universal graphs and universal functions. Ada Arith., 9 (1964), 331–340.CrossRefGoogle Scholar
7.Rado, R.. Universal graphs. In A Seminar in Graph Theory, (eds. Harary, and Beineke, ) (Holt, Rinehart and Winston Co., 1967).Google Scholar
8.Shelah, S.. Notes in combinatorial set theory. Israel J. Math., 14 (1973), 262–277.CrossRefGoogle Scholar
9.Report on the 1980 M. Schweitzer mathematical competition (in Hungarian). Mat. Lapok, 29 (1977–1981), 349–362.Google Scholar