Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T22:43:41.566Z Has data issue: false hasContentIssue false
  • English
  • Français

Upper and lower bound results on the convex hull of integer points in polyhedra

Part of: Discrete geometry

Published online by Cambridge University Press:  26 February 2010

D. A. Morgan
D. A. Morgan
Affiliation:
Dr. D. A. Morgan, Department of Mathematics, University College London, Gower Street, London, WC1E 6BT
Get access

Abstract

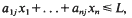In typical linear programming problems, we are concerned with finding non-negative integers {x1,…, xn} that maximize a linear form c1x1 + … + cnxn, subject to a number of linear inequalities, for 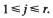The maximum is necessarily attained at one of the vertices of the convex hull of integer points defined by the inequalities, so we have an interest in estimating the number M of these vertices. We give two results; one improving an upper bound result for M of Hayes and Larman concerning the Knapsack polytope, the other an example showing that, in 3-dimensions, it is possible to choose the coefficients aij to obtain a lower bound for M.

MSC classification

Secondary: 52C07: Lattices and convex bodies in $n$ dimensions
Type
Research Article
Information
Mathematika , Volume 38 , Issue 2 , December 1991 , pp. 321 - 328
Copyright
Copyright © University College London 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Barany, I., Howe, R. and Lovasz, L.. On integer points in polyhedra: A lower bound. Preprint, 1989.Google Scholar
2.Cook, W., Hartmann, M., Kannan, R. and McDiarmid, C.. On integer points in polyhedra. Preprint, 1989.Google Scholar
3.Davenport, H.. On the product of three homogeneous linear forms. J. London Math. Soc, 13 (1938), 139–145.CrossRefGoogle Scholar
4.Davenport, H.. On the product of three homogeneous linear forms. Proc. London Math. Soc. (2), 44 (1938), 412–431.Google Scholar
5.Hayes, A. C. and Larman, D. G.. The vertices of the Knapsack polytope. Discrete Applied Mathematics, 6 (1983), 135–138.CrossRefGoogle Scholar
6.McMullen, P.. The maximum numbers of faces of a convex polytope. Mathematika, 17 (1970), 179–184.Google Scholar
7.Rubin, D. S.. On the unlimited number of faces in integer hulls of linear programs with a single constraint. Operations Research, 18 (1970), 940–946.Google Scholar
8.Schrijver, A.. Theory of Linear and Integer Programming (Wiley, Chichester, 1987).Google Scholar