Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T22:16:56.909Z Has data issue: false hasContentIssue false
  • English
  • Français

The values of Mahler measures

Part of: Algebraic number theory: global fields

Published online by Cambridge University Press:  26 February 2010

John D. Dixon  and
Artūras Dubickas
John D. Dixon
Affiliation:
School of Mathematics and Statistics, Carleton University, Ottawa ON K1S 5B6, Canada. E-mail: jdixon@math.carleton.ca
Artūras Dubickas
Affiliation:
Department of Mathematics and Informatics, Vilnius University, Naugarduko 24, Vilnius 2600, Lithuania. E-mail: arturas.dubickas@maf.vu.lt
Get access

Abstract

The set ℳ* of numbers which occur as Mahler measures of integer polynomials and the subset ℳ of Mahler measures of algebraic numbers (that is, of irreducible integer polynomials) are investigated. It is proved that every number α of degree d in ℳ* is the Mahler measure of a separable integer polynomial of degree at most 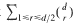with all its roots lying in the Galois closure F of ℚ(α), and every unit in ℳ is the Mahler measure of a unit in F of degree at most 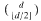over ℚ This is used to show that some numbers considered earlier by Boyd are not Mahler measures. The set of numbers which occur as Mahler measures of both reciprocal and nonreciprocal algebraic numbers is also investigated. In particular, all cubic units in this set are described and it is shown that the smallest Pisot number is not the measure of a reciprocal number.

MSC classification

Secondary: 11R06: PV-numbers and generalizations; other special algebraic numbers; Mahler measure
Type
Research Article
Information
Mathematika , Volume 51 , Issue 1-2 , December 2004 , pp. 131 - 148
Copyright
Copyright © University College London 2004

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Adler, R. L. and Marcus, B.. Topological entropy and equivalence of dynamical systems. Mem. Amer. Math. Soc., 20 (1979), no. 219Google Scholar
2.Boyd, D. W.. Reciprocal polynomials having small measure. Math. Comp., 35 (1980), 13611377.Google Scholar
3.Boyd, D. W.. Inverse problems tor Mahler's measure. In Diophantine Analysis (Loxton, J. and van der Poorten, A., eds.), London Math. Soc. Lecture Notes, 109. Cambridge Univ. Press (Cambridge 1986), 147158.CrossRefGoogle Scholar
4.Boyd, D. W.. Perron units which are not Mahler measures. Ergod. Thoery and Dynamical Sys., 6 (1986), 485–488.CrossRefGoogle Scholar
5.Boyd, D. W.. Reciprocal algebraic integers whose Mahler measures are non-reciprocal. Canad. Math. Bull. 30 (1987), 38.CrossRefGoogle Scholar
6.Dixon, J. D. and Mortimer, B.. Permutation Groups. Springer-Verlag (New York, 1996).Google Scholar
7.Dubickas, A.. Algebraic conjugates outside the unit circle. In New York Trends in Probabilityand Statistics, Vol. 4: Analytic and Probabilistic Methods in Number Theory (Launnčkas, A.et al. eds.), Palanga, 1996, TEV Vilnius (VSP Utrecht, 1997), 11–21.Google Scholar
8.Dubickas, A.. Mahler measures close to an integer. Canad. Math. Bull., 45 (2002), 196–203.CrossRefGoogle Scholar
9.Dubickas, A.. On numbers which are Mahler measures. Monatsh. Math., 141 (2004), 119–126.CrossRefGoogle Scholar
10.Dubickas, A. and Smyth, C. J.. On the Remak height, the Mahler measure, and conjugate sets of algebraic numbers lying on two circles. Proc. Edinburgh Math. Soc., 44 (2001) 1–17.CrossRefGoogle Scholar
11.Edwards, H. M.. Divisor Theory. Birkhauser (Boston, Mass., 1990).CrossRefGoogle Scholar
12.Hecke, E.. Vorlesungen über die Theorie der algebraischen Zahlen. Akad. Verlag. M. B. H..(Leipzig, 1923) (reprinted, Chelsea, New York, 1948).Google Scholar
13.Lehmer, D. H.. Factorization of certain cyclotomic functions. Ann. of Math. (2), 34 (1933). 461–479.CrossRefGoogle Scholar
14.Lind, D. A.. The entropies of topological Mahler shifts and a related class of algebraic integers. Ergod. Theory and Dynamical Sys., 4 (1984), 283–300.CrossRefGoogle Scholar
15.Mahler, K.. On some inequalities for polynomials in several variables. J. London Math. Soc., 37 (1962), 341–344.Google Scholar
16.Serre, J.-P.. Topics in Galois Theory. Jones and Bartlett (Boston, Mass., 1992).Google Scholar
17.Siegel, C. L.. Algebraic integers whose conjugates lie in the unit circle. Duke Math. J., 11 (1944), 597–602.CrossRefGoogle Scholar
18.Smyth, C. J.. On the product of conjugates outside the unit circle of an algebraic integer Bull. London Math. Soc., 3 (1971), 169–175.Google Scholar
19.Smyth, C. J.. Topics in the Theory of Numbers. Ph.D. Thesis, University of Cambridge (1972).Google Scholar
20.Smyth, C. J.. Additive and multiplicative relations connecting conjugate algebraic numbers. J. Number Theory, 23 (1986), 243–254.CrossRefGoogle Scholar
21.van der Waerden, B. L.. Modern Algebra. Frederick Ungar Publ. (New York, 1948).Google Scholar
22.Wielandt, H.. Finite Permutation Groups. Academic Press (New York, 1964).Google Scholar