No CrossRef data available.
Article contents
A variant of the fundamental theorem of projective geometry
Published online by Cambridge University Press: 26 February 2010
Extract
Let K be a field and * an involution of K. Let V and V′ be vector spaces over K of dimensions greater than or equal to 3, and let P(V) and P(F′) denote the projective spaces associated with V and V′ respectively. The fundamental theorem of projective geometry states that a bijection σ between P(V) and P(V′), which preserves the collinearity of points in P(V) and P(V′), is induced by a semi-linear bijection ø between V and V′ with respect to an automorphism α of K. We now consider the following additional structure on V and V′. Let f and f′ be hermitian forms with respect to * on V and V′ respectively; they define twisted polarities in P(V) and P(V′). We prove the following theorem. If there are no self-polar points in P(V) and P(V′) and σ preserves the twisted polarities, then ø is “almost” an isomorphism of the hermitian forms in the sense that
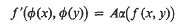
for some non-zero A in K such that A = A*. We give examples of forms f and f′ satisfying the above condition and we illustrate our theorem.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1976

