Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Fowler, Andrew
2011.
Mathematical Geoscience.
Vol. 36,
Issue. ,
p.
331.
Khonina, S. N.
and
Ustinov, A. V.
2017.
Fractional Airy beams.
Journal of the Optical Society of America A,
Vol. 34,
Issue. 11,
p.
1991.
Ustinov, A V
2018.
Analytical features of extended Airy beams.
Journal of Physics: Conference Series,
Vol. 1096,
Issue. ,
p.
012001.
Dovgal, Sergey
de Panafieu, Élie
Ralaivaosaona, Dimbinaina
Rasendrahasina, Vonjy
and
Wagner, Stephan
2024.
The birth of the strong components.
Random Structures & Algorithms,
Vol. 64,
Issue. 2,
p.
170.

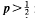 is extended to show that all the zeros of
is extended to show that all the zeros of 