Article contents
Crystal structures of rhodium-containing erlichmanite–laurite solid solutions (Os1–x–yRuxRhyS2: x = 0.09–0.60, y = 0.07–0.10) with unique compositional dependence
Published online by Cambridge University Press: 22 December 2022
Abstract
Rh-rich and Ir-poor erlichmanite–laurite OsS2–RuS2 solid solutions have been discovered at placers in Haraigawa, Misato-machi, Kumamoto, Japan. Microprobe analysis was performed to identify solid solutions containing few sub-components other than Rh. Approximately 10 at.% Rh was found to be present in the solid-solution samples. Structural refinement was performed using four natural samples: Os0.32Ru0.61Rh0.07S2, Os0.49Ru0.43Rh0.08S2, Os0.58Ru0.33Rh0.08S2 and Os0.81Ru0.09Rh0.10S2. The unit-cell parameters for the solid solutions containing Rh from Haraigawa varied from 5.61826(6) to 5.63142(8) Å. The (Os, Ru, Rh)–S distances in the Os1–x–yRuxRhyS2 system were almost constant with a small variation of 0.001 Å. Conversely, the S–S distances varied significantly, with variations approaching 0.1 Å. Rh substitution of Os rather than Ru had a larger impact on the crystal structure. The atomic displacement ellipsoid of both cations and anions was almost spherical, and no elongation along the M–S and S–S bond directions was observed. The bulk Debye temperatures were estimated from the Debye–Waller factor for the sulfide site. The bulk Debye temperatures of pure OsS2 and RuS2 were 688 K and 661 K, respectively, which suggests that the melting point of erlichmanite is higher than that of laurite. The high Debye temperature of OsS2 is inconsistent with the crystallisation of laurite prior to erlichmanite from the primitive magma, which suggests that $f_{\rm S_2}$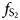 , rather than temperature, is the main cause of the known crystallisation order. The presence of several percent Rh has a significant effect on the thermal stability of OsS2 and lowers the melting point of the erlichmanite solid solution compared to that of the laurite solid solution.
, rather than temperature, is the main cause of the known crystallisation order. The presence of several percent Rh has a significant effect on the thermal stability of OsS2 and lowers the melting point of the erlichmanite solid solution compared to that of the laurite solid solution.
Information
- Type
- Article
- Information
- Copyright
- Copyright © The Author(s), 2022. Published by Cambridge University Press on behalf of The Mineralogical Society of the United Kingdom and Ireland
Footnotes
Associate Editor: František Laufek
References
- 1
- Cited by

