Article contents
Aluminotaipingite-(CeCa), (Ce6Ca3)Al(SiO4)3[SiO3(OH)]4F3, a new member of the cerite-supergroup minerals
Published online by Cambridge University Press: 03 July 2023
Abstract
Aluminotaipingite-(CeCa), (Ce6Ca3)Al(SiO4)3[SiO3(OH)]4F3, is a new member of the cerite-supergroup minerals, whose general chemical formula is A9XM[TO3Ø]7Z3, (A = REE, Ca, Sr, Na and □; X = □, Ca, Na and Fe2+; M = Mg, Fe2+, Fe3+, Al and Mn; T = Si and P; Ø = O and OH; Z = □, OH and F). It was found in cavities of a leucogranitic orthogneiss at the Casette quarry, Montoso, Bagnolo Piemonte, Cuneo Province, Piedmont, Italy. Crystals of aluminotaipingite-(CeCa) are light pink to pink, transparent or semi-transparent, with a vitreous lustre. It forms pyramidal crystals up to 0.07 mm in size and observed forms are {0 0 1}, {1 0 $\bar{2}$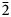 }. The tenacity is brittle, no distinct cleavage is observed and the fracture is uneven. The mineral does not fluoresce in long- or short-wave ultraviolet light. The streak is white. Hardness (Mohs) = 5. The calculated density is 4.476 g cm–3.
}. The tenacity is brittle, no distinct cleavage is observed and the fracture is uneven. The mineral does not fluoresce in long- or short-wave ultraviolet light. The streak is white. Hardness (Mohs) = 5. The calculated density is 4.476 g cm–3.
The mineral is trigonal, space group R3c, with a = 10.658(3), c = 37.865(9) Å, V = 3725(2) Å3 and Z = 6. The eight strongest powder X-ray diffraction lines are [dobs, Å (I, %) (h k l)]: 8.38(29)(0 1 2), 4.499(28)(2 0 2), 3.282(41)(2 1 4), 2.936(100)(0 2 10), 2.816(51)(1 2 8), 2.669(37)(2 2 0), 2.207 (29)(3 0 12) and 1.935(35)(2 3 8). The structure was refined to R =0.0306 for 2297 reflections with I >2σ(I). The crystal structure of aluminotaipingite-(CeCa) contains two nine-fold coordinated sites (A1 and A2), which are occupied mainly by lanthanides, and a third nine-fold coordinated A3 site containing almost equal amounts of lanthanides and Ca. The X site is vacant and at the octahedral M site aluminium prevails over Fe3+. Among the three independent T sites, T2 belongs to a (SiO4)4– anion, whereas T1 and T3 belong to (SiO3OH)3– anions. Fluorine is involved in coordination with the A1 and A3 sites.
- Type
- Article
- Information
- Copyright
- Copyright © The Author(s), 2023. Published by Cambridge University Press on behalf of The Mineralogical Society of the United Kingdom and Ireland
Footnotes
Associate Editor: Anthony R Kampf
References
- 1
- Cited by


