Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-10T10:33:20.643Z Has data issue: false hasContentIssue false
  • English
  • Français

Computer simulation of a microstructure in a potassium feldspar

Published online by Cambridge University Press:  05 July 2018

I. Tsatskis  and
E. K. H. Salje
I. Tsatskis
Affiliation:
Department of Earth Sciences, University of Cambridge, Downing Street, Cambridge, CB2 3EQ, UK
E. K. H. Salje
Affiliation:
Department of Earth Sciences, University of Cambridge, Downing Street, Cambridge, CB2 3EQ, UK Interdisciplinary Research Centre in Superconductivity, University of Cambridge, Madingley Road, Cambridge CB3 0HE, UK
Get access Rights & Permissions [Opens in a new window]

Abstract

Kinetics of atomic ordering in a potassium feldspar is simulated using massively parallel computing. The simulation method is based on the Monte Carlo algorithm for the Al-Si redistribution (the Kawasaki dynamics) combined with the lattice relaxation. The Hamiltonian has the symbolic form

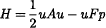
where u represents displacements of atoms from ideal positions, and p the Al and Si occupation numbers. The model is purely elastic; there is no direct interaction between Al and Si atoms. The simulated crystal is a thin film with (010) surfaces and consists of 64 × 64 unit cells; the unit cell defined for the whole film contains slightly more than 4 formula units. The (010) orientation is chosen in order to preserve in the film the main structural feature of feldspars: crankshaft-like sheets formed by four-tetrahedra rings. This makes it possible to observe the Pericline twins only. At the late stage of the kinetic run these twins are clearly seen. The direction for the domain walls is determined by the spontaneous strain and changes with the change of the model parameters; considerable local deviations from this direction are observed.

Keywords

feldsparmicrostructurephase transitionkineticsdomains
Type
Research Article
Information
Mineralogical Magazine , Volume 59 , Issue 397 , December 1995 , pp. 623 - 628
Copyright
Copyright © The Mineralogical Society of Great Britain and Ireland 1995

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

*

Previous name: I. V. Masanskii

References

Binder, K. and Stauffer, D. (1987) A simple introduction to Monte Carlo simulation and some specialized topics. In Applications of the Monte Carlo Method in Statistical Physics. Springer, Berlin, pp. 1–36.CrossRefGoogle Scholar
Bratkovsky, A.M., Salje, E.K.H., Marais, S.C. and Heine, V. (1994a) Theory and computer simulation of tweed texture. Phase Trans., 48, 1–13.CrossRefGoogle Scholar
Bratkovsky, A.M., Salje, E.K.H., and Heine, V. (1994b) Overview of the origin of tweed texture. Phase Trans., 52, 77–84.CrossRefGoogle Scholar
Bratkovsky, A.M., Marais, S.C., Heine, V. and Salje, E.K.H. (1994c) The theory of fluctuations and texture embryos in structural phase transitions mediated by strain. J. Phys.: Condens. Matter, 6, 3679–96.Google Scholar
Brown, W.L. and Parsons, I. (1994) Feldspars in igneous rocks. In Feldspars and their reactions (Parsons, I., ed.). Kluwer, Dordrecht, pp. 449-99.Google Scholar
Catlow, C.R.A. (1988) Computer modelling of silicates. In Physical Properties and Thermodynamic Behaviour of Minerals (Salje, E.K.H., ed.). D. Reidel Publishing Company, Dordrecht, pp. 619-38.Google Scholar
Dove, M. (1988) Molecular dynamics simulations in the solid state sciences. In Physical Properties and Thermodynamic Behaviour of Minerals (Salje, E.K.H., ed.). D. Reidel Publishing Company, Dordrecht, pp. 501-90.Google Scholar
Khachaturyan, A.G. (1983) Theory of Structural Transformations in Solids. Wiley, New York, 574 pp.Google Scholar
Krivoglaz, M.A. (1969) Theory of X-Ray and Thermal Neutron Scattering by Real Crystals. Plenum, New York 405 pp.Google Scholar
Megaw, H.D. (1973) Crystal Structures: A Working Approach. W.B. Saunders Company, Philadelphia, 563 pp.Google Scholar
Parlinski, K., Salje, E.K.H. and Heine, V. (1993a) Annealing of tweed microstructure in high-Tc superconductors studied by a computer simulation. Ada metall. mater., 41, 839–47.CrossRefGoogle Scholar
Parlinski, K., Heine, V. and Salje, E.K.H. (1993ft) Origin of tweed texture in the simulation of a cuprate superconductor. J. Phys.: Condens. Matter, 5, 497–518.Google Scholar
Press, W.H., Flannery, B.P., Teukolsky, S.A. and Vetterling, W.T. (1986) Numerical Recipes: The Art of Scientific Computing. Cambridge University Press, Cambridge, 818 pp.Google Scholar
Putnis, A. (1992) Introduction to Mineral Sciences. Cambridge University Press, Cambridge, 457 pp.CrossRefGoogle Scholar
Salje, E.K.H. (1992) Application of Landau theory for the analysis of phase transitions in minerals. Physics Reports, 215, 49–99.CrossRefGoogle Scholar
Salje, E.K.H. and Parlinski, K. (1991) Microstructures in the high-Tc superconductors. Superconductor Science and Technology, 4, 93–7.CrossRefGoogle Scholar
Salje, E., Kuscholke, B. and Wruck, B. (1985) Domain wall formation in minerals: I. Theory of twin boundary shapes in Na-feldspar. Phys. Chem. Minerals, 12, 132–40.CrossRefGoogle Scholar
Sapriel, J. (1975) Domain-wall orientations in ferroelastics. Phys. Rev. B, 12, 5128–40.CrossRefGoogle Scholar
Smith, J.V. and Brown, W.L. (1988) Feldspar minerals, vol. 1. Springer, Berlin, 828 pp.CrossRefGoogle Scholar
Zangwill, A. (1988) Physics at Surfaces. Cambridge University Press, Cambridge, 454 pp.CrossRefGoogle Scholar