Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-27T07:24:10.612Z Has data issue: false hasContentIssue false
  • English
  • Français

Constraints on the Equations of State of stiff anisotropic minerals: rutile, and the implications for rutile elastic barometry

Published online by Cambridge University Press:  22 April 2019

Gabriele Zaffiro ,
Ross J. Angel Open the ORCID record for Ross J. Angel [Opens in a new window]  and
Matteo Alvaro
Gabriele Zaffiro
Affiliation:
Department of Earth and Environmental Sciences, University of Pavia, Via A. Ferrata, 1 I-27100, Pavia, Italy
Ross J. Angel*
Affiliation:
Department of Earth and Environmental Sciences, University of Pavia, Via A. Ferrata, 1 I-27100, Pavia, Italy
Matteo Alvaro
Affiliation:
Department of Earth and Environmental Sciences, University of Pavia, Via A. Ferrata, 1 I-27100, Pavia, Italy
*
*Author for correspondence: Ross J. Angel, Email: rossjohnangel@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

We present an assessment of the thermo-elastic behaviour of rutile based on X-ray diffraction data and direct elastic measurements available in the literature. The data confirms that the quasi-harmonic approximation is not valid for rutile because rutile exhibits substantial anisotropic thermal pressure, meaning that the unit-cell parameters change significantly along isochors. Simultaneous fitting of both the diffraction and elasticity data yields parameters of KTR0= 205.14(15) GPa, KSR0= 207.30(14) GPa, 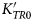$K_{TR0}^{\prime} $= 6.9(4) in a 3rd-order Birch-Murnaghan Equation of State for compression, αV0= 2.526(16) × 10–5 K–1, Einstein temperature θE = 328(12) K, Anderson-Grüneisen parameter δT = 7.6(6), with a fixed thermal Grüneisen parameter γ = 1.4 to describe the thermal expansion and variation of bulk modulus with temperature at room pressure. This Equation of State fits all of the available data up to 7.3 GPa at room temperature, and up to 1100 K at room pressure within its uncertainties. We also present a series of formulations and a simple protocol to obtain thermodynamically consistent Equations of State for the volume and the unit-cell parameters for stiff materials, such as rutile. In combination with published data for garnets, the Equation of State for rutile indicates that rutile inclusions trapped inside garnets in metamorphic rocks should exhibit negative residual pressures when measured at room conditions.

Keywords

rutilehigh pressurehigh temperatureelasticityP–V–T–K fitEosFitnegative residual pressures
Type
Article
Information
Mineralogical Magazine , Volume 83 , Issue 3 , June 2019 , pp. 339 - 347
Copyright
Copyright © Mineralogical Society of Great Britain and Ireland 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Associate Editor: Andrew G Christy

References

Adams, H.G., Cohen, L.H. and Rosenfeld, J.L. (1975) Solid inclusion piezothermometry I: comparison dilatometry. American Mineralogist, 60, 574–583.Google Scholar
Al-Khatatbeh, Y., Lee, K.K. and Kiefer, B. (2009) High-pressure behavior of TiO2 as determined by experiment and theory. Physical Review B, 79, 134114.Google Scholar
Al'tshuler, L.V., Podurets, M.A., Simakov, G.V. and Trunin, R.F. (1973) High-density forms of fluorite and rutile. Soviet Physics Solid State, 15, 969–971.Google Scholar
Anderson, O.L. (1995) Equations of State of Solids for Geophysics and Ceramic Science. Oxford University Press, Oxford, UK, 432 pp.Google Scholar
Anderson, O.L., Isaak, D. and Oda, H. (1992) High-temperature elastic constant data on minerals relevant to geophysics. Reviews of Geophysics, 30, 57–90.Google Scholar
Angel, R.J., Gonzalez-Platas, J. and Alvaro, M. (2014) EosFit7c and a Fortran module (library) for equation of state calculations. Zeitschrift für Kristallographie, 229, 405–419.Google Scholar
Angel, R.J., Nimis, P., Mazzucchelli, M.L., Alvaro, M. and Nestola, F. (2015) How large are departures from lithostatic pressure? Constraints from host-inclusion elasticity. Journal of Metamorphic Geology, 33, 801–813.Google Scholar
Angel, R.J., Mazzucchelli, M.L., Alvaro, M. and Nestola, F. (2017) EosFit-Pinc: A simple GUI for host-inclusion elastic thermobarometry. American Mineralogist, 102, 1957–1960.Google Scholar
Angel, R.J., Alvaro, M. and Nestola, F. (2018) 40 years of mineral elasticity: a critical review and a new parameterisation of Equations of State for mantle olivines and diamond inclusions. Physics and Chemistry of Minerals, 45, 95–113.Google Scholar
Angel, R.J., Murri, M., Mihailova, B. and Alvaro, M. (2019) Stress, strain and Raman shifts. Zeitschrift für Kristallographie, 234, 129–140.Google Scholar
Arashi, H. (1992) Raman spectroscopic study of the pressure-induced phase transition in TiO2. Journal of Physics and Chemistry of Solids, 53, 355–359.Google Scholar
Barron, T.H.K., Collins, J.G. and White, G.K. (1980) Thermal expansion of solids at low temperatures. Advances in Physics, 29, 609–730.Google Scholar
Birch, F. (1947) Finite elastic strain of cubic crystals. Physical Review, 71, 809–824.Google Scholar
Burdett, J.K., Hughbanks, T., Miller, G.J., Richardson, J.W. Jr and Smith, J.V. (1987) Structural-electronic relationships in inorganic solids: powder neutron diffraction studies of the rutile and anatase polymorphs of titanium dioxide at 15 and 295 K. Journal of the American Chemical Society, 109, 3639–3646.Google Scholar
Campomenosi, N., Mazzucchelli, M.L., Mihailova, B., Scambelluri, M., Angel, R.J., Nestola, F., Reali, A. and Alvaro, M. (2018) How geometry and anisotropy affect residual strain in host inclusion system: coupling experimental and numerical approaches. American Mineralogist, 103, 2032–2035.Google Scholar
Dubrovinskaia, N.A., Dubrovinsky, L.S., Ahuja, R., Prokopenko, V.B., Dmitriev, V., Weber, H.-P., Osorio-Guillen, J.M. and Johansson, B. (2001) Experimental and theoretical identification of a new high-pressure TiO2 polymorph. Physical Review Letters, 87, 275501.Google Scholar
Ferrero, S. and Angel, R.J. (2018) Micropetrology: are inclusions grains of truth? Journal of Petrology, 59, 1671–1700.Google Scholar
Fritz, I.J. (1974) Pressure and temperature dependences of the elastic properties of rutile (TiO2). Journal of the Physics and Chemistry of Solids, 35, 817–826.Google Scholar
Gerward, L. and Staun Olsen, J. (1997) Post-rutile high-pressure phases in TiO2. Journal of Applied Crystallography, 30, 259–264.Google Scholar
Grüneisen, E. (1926) Zustand des festen Körpers. Handbuch der Physik, 1, 1–52.Google Scholar
Hazen, R.M. and Finger, L.W. (1981) Bulk moduli and high-pressure crystal structures of rutile-type compounds. Journal of Physics and Chemistry of Solids, 42, 143–151.Google Scholar
Hellfrich, G. and Connolly, J.A.D. (2009) Physical contradictions and remedies using simple polythermal equations of state. American Mineralogist, 94, 1616–1619.Google Scholar
Henderson, C.M.B., Knight, K.S. and Lennie, A.R. (2009) Temperature dependence of rutile (TiO2) and geikielite (MgTiO3) structures determined using neutron powder diffraction. The Open Mineralogy Journal, 3, 1–11.Google Scholar
Holland, T.J.B. and Powell, R. (2011) An improved and extended internally consistent thermodynamic dataset for phases of petrological interest, involving a new equation of state for solids. Journal of Metamorphic Geology, 29, 333–383.Google Scholar
Hummer, D.R., Heaney, P.J. and Post, J.E. (2007) Thermal expansion of anatase and rutile between 300 and 575 K using synchrotron powder X-ray diffraction. Powder Diffraction, 22, 352–357.Google Scholar
Isaak, D.G., Carnes, J.D., Anderson, O.L., Cynn, H. and Hake, E. (1998) Elasticity of TiO2 rutile to 1800 K. Physics and Chemistry of Minerals, 26, 31–43.Google Scholar
Kirby, R.K. (1967) Thermal expansion of rutile from 100 to 700 K. Journal of Research of the National Bureau of Standards – A. Physics and Chemistry, 71A, 363–369.Google Scholar
Kohn, M.J. (2014) “Thermoba-Raman-try”: Calibration of spectroscopic barometers and thermometers for mineral inclusions. Earth and Planetary Science Letters, 388, 187–196.Google Scholar
Kojitani, H., Yamazaki, M., Kojima, M., Inaguma, Y., Mori, D. and Akaogi, M. (2018) Thermodynamic investigation of the phase equilibrium boundary between TiO2 rutile and its α-PbO2-type high-pressure polymorph. Physics and Chemistry of Minerals, 45, 963–980.Google Scholar
Kroll, H., Kirfel, A., Heinemann, R. and Barbier, B. (2012) Volume thermal expansion and related thermophysical parameters in the Mg,Fe olivine solid-solution series. European Journal of Mineralogy, 24, 935–956.Google Scholar
Kudoh, Y. and Takeda, H. (1986) Single crystal X-ray diffraction study on the bond compressibility of fayalite, Fe2SiO4 and rutile, TiO2 under high pressure. Physica B, 139 & 140, 333–336.Google Scholar
Lan, T., Li, C.W., Hellman, O., Kim, D.S., Munoz, J.A., Smith, H., Abernathy, D.L. and Fultz, B. (2015) Phonon quarticity induced by changes in phonon-tracked hybridization during lattice expansion and its stabilization of rutile TiO2. Physical Review B, 92, 054304.Google Scholar
Mammone, J.F., Sharma, S.K. and Nicol, M. (1980) Raman study of rutile (TiO2) at high pressures. Solid State Communications, 34, 799–802.Google Scholar
Manghnani, M.H. (1969) Elastic constants of single-crystal rutile under pressures to 7.5 kilobars. Journal of Geophysical Research, 74, 4317–4328.Google Scholar
Manghnani, M.H., Fisher, E.S. and Brower, W.S. Jr (1972) Temperature dependence of the elastic constants of single-crystal rutile between 4 and 583 K. Journal of Physics and Chemistry of Solids, 33, 2149–2159.Google Scholar
McQueen, R.G., Jamieson, J.C. and Marsh, S.P. (1967) Shock-wave compression and X-ray studies of titanium dioxide. Science, 155, 1401–1404.Google Scholar
Meagher, E.P. and Lager, G.A. (1979) Polyhedral thermal expansion in the TiO2 polymorphs; refinement of the crystal structures of rutile and brookite at high temperature. The Canadian Mineralogist, 17, 77–85.Google Scholar
Mei, Z.G., Wang, Y., Shang, S. and Liu, Z.K. (2014) First-principles study of the mechanical properties and phase stability of TiO2. Computational Materials Science, 83, 114–119.Google Scholar
Meinhold, G. (2010) Rutile and its applications in earth sciences. Earth-Science Reviews, 102, 1–28.Google Scholar
Milani, S., Nestola, F., Alvaro, M., Pasqual, D., Mazzucchelli, M.L., Domeneghetti, M.C. and Geiger, C. (2015) Diamond–garnet geobarometry: The role of garnet compressibility and expansivity. Lithos, 227, 140–147.Google Scholar
Milani, S., Angel, R.J., Scandolo, L., Mazzucchelli, M.L., Boffa-Ballaran, T., Klemme, S., Domeneghetti, M.C., Miletich, R., Scheidl, K.S., Derzsi, M., Tokar, K., Prencipe, M., Alvaro, M. and Nestola, F. (2017) Thermo-elastic behaviour of grossular garnets at high pressures and temperatures. American Mineralogist, 102, 851–859.Google Scholar
Ming, L.C. and Manghnani, M.H. (1979) Isothermal compression of TiO2 (rutile) under hydrostatic pressure to 106 kbar. Journal of Geophysical Research, 84, 4777–4779.Google Scholar
Murri, M., Mazzucchelli, M.L., Campomenosi, N., Korsakov, A.V., Prencipe, M., Mihailova, B., Scambelluri, M., Angel, R.J. and Alvaro, M. (2018) Raman elastic geobarometery for anisotropic mineral inclusions. American Mineralogist, 103, 1869–1872.Google Scholar
Nicol, M. and Fong, M.Y. (1971) Raman spectrum and polymorphism of titanium dioxide at high pressures. Journal of Chemical Physics, 54, 3167–3170.Google Scholar
Nye, J.F. (1957) Physical Properties of Crystals. Oxford University Press, Oxford, 329 pp.Google Scholar
Rao, K.K., Naidu, S.N. and Iyengar, L. (1970) Thermal expansion of rutile and anatase. Journal of the American Ceramic Society, 53, 124–126.Google Scholar
Rosenfeld, J.L. and Chase, A.B. (1961) Pressure and temperature of crystallization from elastic effects around solid inclusion minerals? American Journal of Science, 259, 519–541.Google Scholar
Sato, Y. (1977) Equation of state of mantle minerals determined through high-pressure X-ray study. Pp 307–323 in: High-Pressure Research: Applications in Geophysics (Manghnani, M. H. and Akimoto, S.-I., editors). American Geophysical Union, Washington DC.Google Scholar
Stangarone, C., Alvaro, M., Angel, R., Prencipe, M. and Mihailova, B.D. (2019) Determination of the phonon-mode Grüneisen tensors of zircon by DFT simulations. European Journal of Mineralogy, doi: 10.1127/ejm/2019/0031-2851.Google Scholar
Sugiyama, K. and Takeuchi, Y. (1991) The crystal structure of rutile as a function of temperature up to 1600°C. Zeitschrift für Kristallographie, 194, 305–313.Google Scholar
Syono, Y., Kusaba, K., Kikuchi, M., Fukuoka, K. and Goto, T. (1987) Shock-induced phase transitions in rutile single crystal. Pp 385–392 in: High-Pressure Research in Mineral Physics (Manghnani, M. H. and Syono, Y., editors). American Geophysical Union, Washington DC, USA.Google Scholar
Van Westrenen, W., Frank, M.R., Hanchar, J.M., Fei, Y.W., Finch, R.J. and Zha, C.S. (2004) In situ determination of the compressibility of synthetic pure zircon (ZrSiO4) and the onset of the zircon-reidite phase transition. American Mineralogist, 89, 197–203.Google Scholar
Wang, L., Wang, H.J. and Li, T. (2013) In situ high temperature X-ray diffraction study of anatase and rutile. Acta Physica Sinica, 62, 146402.Google Scholar
Zack, T. and Kooijman, E. (2017) Petrology and geochronology of rutile. pp. 433–467 in: Petrochronology: Methods and Applications (Kohn, M. J., Engi, M. and Lanari, P., editors). Reviews in Mineralogy and Geochemistry, 83. Mineralogical Society of America and the Geochemical Society, Chantilly, Virginia, USA.Google Scholar
Zaffiro, G., Angel, R.J., Alvaro, M., Prencipe, M. and Stangarone, C. (2018) P-V-T-Ks Equations of State for zircon and rutile. Geophysical Research Abstract, 20, 6952.Google Scholar
Zhang, Y. (1998) Mechanical and phase equilibria in inclusion–host systems. Earth and Planetary Science Letters, 157, 209–222.Google Scholar
Supplementary material: File

Zaffiro et al. supplementary material

Zaffiro et al. supplementary material 1

Download Zaffiro et al. supplementary material(File)
File 10.5 KB