Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T06:55:13.266Z Has data issue: false hasContentIssue false
  • English
  • Français

Description and crystal structure of domerockite, Cu4(AsO4)(AsO3OH)(OH)3·H2O, a new mineral from the Dome Rock Mine, South Australia

Published online by Cambridge University Press:  05 July 2018

P. Elliott ,
U. Kolitsch ,
A. C. Willis  and
E. Libowitzky
P. Elliott*
Affiliation:
School of Earth and Environmental Sciences, The University of Adelaide, Adelaide, South Australia 5005, Australia
U. Kolitsch
Affiliation:
Mineralogisch-Petrographische Abt., Naturhistorisches Museum, Burgring 7, A-1010 Vienna, Austria Institut für Mineralogie und Kristallographie, Geozentrum, Universität Wien, Althanstrasse 14, A-1090 Vienna, Austria
A. C. Willis
Affiliation:
Research School of Chemistry, The Australian National University, Australian Capital Territory 0200, Australia
E. Libowitzky
Affiliation:
Institut für Mineralogie und Kristallographie, Geozentrum, Universität Wien, Althanstrasse 14, A-1090 Vienna, Austria
*
* E-mail: peter.elliott@adelaide.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

Domerockite, Cu4(AsO4)2(AsO3OH)(OH)3·H2O, is a new mineral from the Dome Rock Mine, South Australia. It occurs as aggregates of bluish green, equant to short prismatic and tabular crystals up to 0.3 mm long and 0.2 mm across. Domerockite is translucent, with a vitreous lustre and pale green streak. It displays no fluorescence under UV irradiation. The mineral is brittle with an uneven fracture, a Mohs hardness of ∼3 and a calculated density of 4.44 g/cm3 (based on the structure refinement). Optically, it is biaxial negative, with α = 1.798(4), β = 1.814(4), γ = 1.817(4), 2Vcalc. = 46°; pleochroism is very weak; X pale greenish yellow, Y greenish blue, Z greenish blue; absorption X < Y = Z; orientation is uncertain. Chemical analysis by electron microprobe gave CuO 52.04, ZnO 0.78, BaO 0.11, As2O537.67, P2O50.32, SiO20.24, H2O 8.84, total 100.00 wt.%, with H2O calculated by difference. The empirical chemical formula is (Cu3.94, Zn0.06)Σ4.00H0.91(As1.97, P0.03, Si0.02)Σ2.02O8(OH)3.00˙H2O based on 12 oxygen atoms.

Domerockite is triclinic, space group P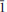, with a = 5.378(11), b = 8.962(18) c = 9.841(2) Å, α = 75.25(3), β = 83.56(3), γ = 79.97(3)°, V = 450.5(16) Å3 and Z = 2. The eight strongest lines in the X-ray powder diffraction pattern are [d (Å), (I)(hkl)]: 4.716 (30)(101, 002, 111), 3.697 (25)(121), 3.605 (30)(120, 12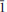), 3.119 (60)(12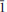), 3.073 (100)(1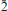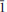), 2.856 (40)(02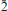, 030), 2.464 (50)(212, 1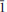3), 2.443 (40)(014). The crystal structure of domerockite has been solved by direct methods and refined to an R index of 7.44% using 2635 observed reflections. The structure comprises [Cuφ4] (φ = O, OH) chains of edge-sharing sharing, distorted octahedra that extend along [10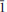] and are decorated by AsO4 tetrahedra to form sheets in the (010) plane. Dimers of edge-sharing [CuO4(OH)(H2O)] octahedra share corners with dimers of edge-sharing [CuO4(OH)] square pyramids to form zigzag chains which extend along [101]. The chains lie between and link to the sheets by sharings corners of octahedra, square pyramids and tetrahedra to form a heteropolyhedral framework.

Keywords

domerockitenew mineral speciescopper arsenatecrystal structureDome Rock mine
Type
Research Article
Information
Mineralogical Magazine , Volume 77 , Issue 4 , June 2013 , pp. 509 - 522
Copyright
Copyright © The Mineralogical Society of Great Britain and Ireland 2013

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baur, W.H. (1981) Interatomic distance predictions for computer simulation of crystal structures. Pp. 31–52. in: Structure and Bonding in Crystals II (M. O’Keeffe and A. Navrotsky, editors). Academic Press, New York.CrossRefGoogle Scholar
Bayliss, P., Lawrence, L.J. and Watson, D. (1966) Rare copper arsenates from Dome Rock, South Australia. Australian Journal of Science, 29, 145–146.Google Scholar
Blissett, A.H. (1972) Recovery of copper at the Dome Rock Mine, South Australia. Department of Mines, Mineral Resources Review, 137, 104–110.Google Scholar
Brese, N.E. and O’Keeffe, M. (1991) Bond-valence parameters for solids. Acta Crystallographica, B47, 192–197.CrossRefGoogle Scholar
Brown, I.D. (1996) VALENCE: a program for calculating bond-valences. Journal of Applied Crystallography, 29, 479–480.CrossRefGoogle Scholar
Brown, I.D. and Altermatt, D. (1985) Bond-valence parameters obtained from a systematic analysis of the inorganic crystal structure database. Acta Crystallographica, B41, 244–247.CrossRefGoogle Scholar
Burns, P.C. and Hawthorne, F.C. (1995) Coordinationgeometry structural pathways in Cu2+ oxysalt minerals. The Canadian Mineralogist, 33, 889–905.Google Scholar
Burns, P.C. and Hawthorne, F.C. (1996) Static and dynamic Jahn-Teller effects in Cu2+ oxysalts. The Canadian Mineralogist, 34, 1089–1105.Google Scholar
Campana, B. and King, D. (1958) Regional geology and mineral resources of the Olary Province. Geological Survey of South Australia, Bulletin 34. 133 pp.Google Scholar
Cooper, M.A., Hawthorne, F.C. and Černý, P. (2009) The crystal structure of ercitite, Na2(H2O)4[Mn3+ 2 (OH)2(PO4)2], and its relation to bermanite, Mn2+(H2O)4[Mn3+ 2 (OH)2(PO4)2]. The Canadian Mineralogist, 47, 173–180.CrossRefGoogle Scholar
Dickinson, S.B. (1942) The structural control of ore deposition in some South Australian copperfields. Geological Survey of South Australia, Bulletin, 20, 1–39.Google Scholar
Eby, R.K. and Hawthorne, F.C. (1990) Clinoclase and the geometry of [5]-coordinate Cu2+ in minerals. Acta Crystallographica, C46, 2291–2294.Google Scholar
Eby, R.K. and Hawthorne, F.C. (1993) Structural relations in copper oxysalt minerals. I. Structural hierarchy. Acta Crystallographica, B49, 28–56.CrossRefGoogle Scholar
Elliott, P., Brugger, J., Caradoc-Davies, T. and Pring, A. (2013) Hylbrownite, Na3MgP3O10·12H2O, a new triphosphate mineral from the Dome Rock Mine, South Australia: description and crystal structure. Mineralogical Magazine, 77, 385–398.CrossRefGoogle Scholar
Ferraris, G. and Ivaldi, G. (1984) X–OH and O-H_O bond lengths in protonated oxoanions. Acta Crystallographica, B40, 1–6.Google Scholar
Jahn, H.A. and Teller, E. (1937) Stability of polyatomic molecules in degenerate electronic states. Proceedings of the Royal Society, Series A, 161, 220–236.Google Scholar
Kampf, A.R. and Moore, P.B. (1976) The crystal structure of bermanite, a hydrated manganese phosphate. American Mineralogist, 61, 1241–1248.Google Scholar
Kleeman, A.W. and Milnes, A.R. (1973) Phosphorian lavendulan from Dome Rock mine, South Australia. Transactions of the Royal Society of South Australia, 97, 135–137.Google Scholar
Krause, W., Belendorff, K., Bernhardt, H.-J., McCammon, C., Effenberger, H. and Mikenda, W. (1998) Crystal chemistry on the tsumcorite-group minerals. New data on ferrilotharmeyerite, tsumcorite, thometzekite, mounanaite, helmutwinklerite, and a redefinition of gartrellite. European Journal of Mineralogy, 10, 179–206.CrossRefGoogle Scholar
Le Bail, A., Duroy, H. and Fourquet, J.L. (1988) Abinitio structure determination of LiSbWO6 by X-ray powder diffraction. Materials Research Bulletin, 23, 447–452.CrossRefGoogle Scholar
Libowitzky, E. (1999) Correlation of O-H stretching frequencies and O-H···O hydrogen bond lengths in minerals. Monatshefte für Chemie, 130, 1047–1059.CrossRefGoogle Scholar
Magalha˜es, M.C.F., Pedrosa de Jesus, J.D. and Williams, P.A. (1988) The chemistry of formation of some secondary arsenate minerals of Cu(II), Zn(II) and Pb(II). Mineralogical Magazine, 52, 679–690.CrossRefGoogle Scholar
Mandarino, J.A. (1981) The Gladstone-Dale relationship: Part IV: The compatibility concept and its application. The Canadian Mineralogist, 19, 441–450.Google Scholar
Mawson, D. (1923) The Dome Rock Copper Mine. Unpublished report for the Dome Rock Copper Mining Co. N.L.Google Scholar
Nickel, E.H. and Birch, W.D. (1988) Cobaltaustinite – a new arsenate mineral from Dome Rock, South Australia. Australian Mineralogist, 3, 53–57.Google Scholar
Otwinowski, Z. and Minor, W. (1997) Processing X-ray diffraction data collected in oscillation mode. Pp. 307–326. in Methods in Enzymology, Volume 276: Macromolecular Crystallography, part A (C.W. Carter, Jr. and R.M. Sweet, editors). Academic Press, New York.Google Scholar
Otwinowski, Z., Borek, D., Majewski, W. and Minor, W. (2003) Multiparametric scaling of diffraction intensities. Acta Crystallographica, A59, 228–234.CrossRefGoogle Scholar
Pouchou, J.L. and Pichoir, F. (1985) "PAP" f(rZ) procedure for improved quantitative microanalysis. Pp. 104–106. in: Microbeam Analysis (J.T. Armstrong, editor). San Francisco Press, San Francisco, California, USA.Google Scholar
Ryall, W.R. and Segnit, E.R. (1976) Minerals of the oxidized zone of the Dome Rock copper deposit, South Australia. Australian Mineralogist, 2, 5–8.Google Scholar
Segnit, E.R. (1978) Further minerals from the Dome Rock Mine, South Australia. Australian Mineralogist, 2, 73–74.Google Scholar
Shannon, R.D. and Calvo, C. (1973) Refinement of the crystal structure of low temperature Li3VO4 and analysis of mean bond lengths in phosphates, arsenates, and vanadates. Journal of Solid State Chemistry, 6, 538–549.CrossRefGoogle Scholar
Shape Software (2004) SHAPE for Windows and Macintosh V 7.1.2, Kingsport, Tennessee, USA.Google Scholar
Sheldrick, G.M. (2008) A short history of SHELX. Acta Crystallographica, A64, 112–122.CrossRefGoogle Scholar
Warne, K.R. (1970) The Dome Rock Copper Mine. South Australia Department of Mines, Mineral Resources Review, 129, 129–141.Google Scholar
Williams, K.L. and Edwards, A.B. (1960) Gossan-like outcrops and oxidized ore from Dome Rock Mine and it’s environs. C.S.I.R.O. Mineragraphic Investigations, Report Number 808.Google Scholar
Wilson, A.J.C. (editor) (1992) International Tables for Crystallography, Vol. C. Kluwer Academic, Dordrecht, The Netherlands, 883 pp.Google Scholar
Yang, H., Costin, G., Keogh, J., Lu, R. and Downs, R.T. (2007) Cobaltaustinite, CaCo(AsO4)(OH). Acta Crystallographica, E63, i53–i55.Google Scholar
Yvon, K., Jeitschko, W. and Parthé, E. (1977) LAZY PULVERIX, a computer program, for calculating X-ray and neutron diffraction powder patterns. Journal of Applied Crystallography, 10, 73–74.CrossRefGoogle Scholar