On the application of the IMA−CNMNC dominant-valency rule to complex mineral compositions

Abstract

Mineral species should be identified by an end-member formula and by using the dominant-valency rule as recommended by the IMA–CNMNC. However, the dominant-end-member approach has also been used in the literature. These two approaches generally converge, but for some intermediate compositions, significant differences between the dominant-valency rule and the dominant end-member approach can be observed. As demonstrated for garnet-supergroup minerals, for example, the end-member approach is ambiguous, as end-member proportions strongly depend on the calculation sequence. For this reason, the IMA–CNMNC strongly recommends the use of the dominant-valency rule for mineral nomenclature, because it alone may lead to unambiguous mineral identification. Although the simple application of the dominant-valency rule is successful for the identification of many mineral compositions, sometimes it leads to unbalanced end-member formulae, due to the occurrence of a coupled heterovalent substitution at two sites along with a heterovalent substitution at a single site. In these cases, it may be useful to use the site-total-charge approach to identify the dominant root-charge arrangement on which to apply the dominant-constituent rule. The dominant-valency rule and the site-total-charge approach may be considered two procedures complementary to each other for mineral identification. Their critical point is to find the most appropriate root-charge and atomic arrangements consistent with the overriding condition dictated by the end-member formula. These procedures were approved by the IMA−CNMNC in May 2019.

Introduction

The development of a nomenclature to identify and classify minerals is a fundamental step to understand the processes that govern mineral diversity and has direct implications on petrogenetic and provenance information. For example, ambiguity in the naming of a mineral species hinders direct comparison of minerals originating from different types of deposits.

A fundamental criterion for mineral nomenclatures (e.g. Hawthorne et al., 1995; Bayliss et al., 2005; Mills et al., 2009) is based on the dominance of a chemical constituent (i.e. ions, vacancies, molecular groups, or atom groups with the same valency state; Nickel and Grice, 1998; Hatert and Burke, 2008) of the dominant valency state at a given crystallographic site. This criterion stems from the application of the dominant-valency rule, which is an extension of the dominant-constituent rule (Hatert and Burke, 2008). Along with valency-imposed double site-occupancy, these two rules may identify a mineral species and its charge-balanced end-member formula as defined by Hawthorne (2002).

However, important aspects need to be clarified when this criterion is applied to minerals of complex mixed compositions. Firstly, a mineral should be identified for the most abundant constituent of the dominant valency state, and not for the most abundant end-member. Indeed, mineral species identified by the dominant valence may not correspond to the dominant end-member component. Secondly, complex coupled substitution mechanisms may lead to compositions which are not directly identified (i.e. an end-member formula is not identified) with the simple application of the dominant-valency rule; in those cases, an extension of the rule may be used (Bosi, 2018).

This study aims at explicitly addressing these issues and at suggesting a coherent procedure to identify mineral species based exclusively on the dominant-valency and dominant-constituent rules, which are currently recommended by the Commission on New Minerals, Nomenclature and Classification (CNMNC) of the International Mineralogical Association (IMA). The following nomenclature proposal was approved by the IMA−CNMNC in May 2019 (Miyawaki et al., 2019).

Dominant-valency rule versus dominant end-member approach

Usually, two approaches could be used to distinguish mineral species: (1) the dominant-valency approach, which identifies mineral species by determining the dominant root-charge arrangement (e.g. Hawthorne, 2002); (2) the dominant-end-member approach, which identifies species by determining the most abundant end-member component (e.g. Bulakh, 2010; Dolivo-Dobrovol'sky, 2010).

These two approaches may converge to the same mineral name in species with chemical substitutions at a single site or at two sites, when the dominant ion of the site-dominant valence state is also the site-dominant ion. Consider the following two examples: (1) the hypothetical composition ^[8](Ca_0.60Na_0.25K_0.15)_Σ1.00^[4](Al_1.60Si_2.40)_Σ4.00O₈ is dominated by the root-charge arrangement (R ²⁺)(R ³⁺₂R ⁴⁺₂)O₈ (60%) corresponding to anorthite CaAl₂Si₂O₈, which is also the most abundant end-member (60%) with respect to albite, NaAlSi₃O₈ (25%) and ‘K-feldspar’, KAlSi₃O₈ (15%); (2) the composition ^[8](Ca_0.35Na_0.40K_0.25)^[4](Al_1.35Si_2.65)O₈ is dominated by the root-charge arrangement (R ⁺)(R ³⁺R ⁴⁺₃)O₈ (65%) corresponding to albite (Na > K), which is also the most abundant end-member (40%) with respect to anorthite (35%) and ‘K-feldspar’ (25%).

The dominant-valency approach and dominant-end-member approach do not converge to the same mineral name in the case of coupled heterovalent substitutions coupled at two sites, associated with homovalent substitutions at one site, leading to a situation where one site-dominant ion is not the dominant ion of the dominant valence state. Consider the composition ^[8](Ca_0.40Na_0.35K_0.25)^[4](Al_1.40Si_2.60)O₈: on the basis of the dominant-valency rule, the dominant root-charge arrangement is (R ⁺)(R ³⁺R ⁴⁺₃)O₈ (60%) as the monovalent cations, Na and K, are dominant at the [8]-fold coordinated site. Thus, the mineral species is identified as albite because the Na content is larger than the K content (dominant-constituent rule). On the other hand, on the basis of the dominant-end-member approach, the mineral would be anorthite as the proportion of this end-member (40%) is dominant over albite (35%) and ‘K-feldspar’ (25%). These relations can be graphically illustrated by ternary diagrams (Fig. 1). Plotting the chemical compositions of the [8]-fold site in a diagram with Ca²⁺, Na⁺ and K⁺ placed at each corner, the typical boundary limits crossing at the centre of the diagram (33% of each component) will represent the dominant-end-member approach (Fig. 1a), whereas the boundary limits are displaced for the dominant-valency approach as follows: 25% for the component Ca²⁺, 37.5% for both Na⁺ and K⁺ (Fig. 1b). Note that the dominant-end-member approach and the dominant-valency rule diverge when mineral compositions occur in the grey triangular area of Fig. 1b. This divergence area is even smaller as the miscibility gap of the feldspar diagram covers most of the grey triangular surface (Fig. 1c).

Fig. 1. Diagram for discriminating anorthite, albite and ‘K-feldspar’ according to the dominant-end-member approach (a) and the dominant-valency rule (b). In (c) the ternary miscibility gap calculated for P = 10 kbar and T = 1200°C (dashed black line) using the method of Kroll et al. (1993), is shown. Solid/dashed red lines are consistent with the dominant-end-member approach, whereas the solid blue lines are consistent with the dominant-valency rule. The grey colour highlights the area where the dominant-end-member approach and the dominant-valency rule diverge.

This simple example demonstrates that a mineral species identified by the dominant-valency approach may not correspond to that identified by the dominant-end-member approach. It is likely that the dominant-valency rule and the end-member approach would give the same identification in many (simple) cases, but there are other cases in which they do not. In these cases the dominant-valency rule should always prevail and mixed mineral nomenclatures, relying on both the dominant-valency rule and the dominant-end-member approach, should be avoided.

An important reason to avoid the identification of a mineral species on the basis of end-member components is that this approach may be ambiguous, not only when new species belonging to poorly characterised groups are discovered, but even when the end-member formulae of all species in the group are known. Indeed, as demonstrated by Rickwood (1968), it is impossible to find a unique algebraic solution for a formula identification, when the number of end-members is higher than the number of independent chemical components. In fact, the results will depend strongly on a specific sequence of calculating end-member proportions, as demonstrated for reciprocal solutions in the garnet or spinel supergroups (e.g. Rickwood, 1968; Grew et al., 2013). An informative example of definition of a meaningless mineral phase is found in Putirka (2016), who identifies a hypothetical new amphibole (‘aluminous kaersutite’) inconsistent with existing nomenclature rules (Hawthorne et al., 2012). Consequently, the end-member approach is ambiguous in mineral nomenclature, although the calculation of end-member proportions is currently an important step for application of thermodynamics to mineral systems and for petrologic studies.

Application of the dominant-valency rule to complex mineral compositions: the site-total-charge approach

The site-total-charge approach

As the sequential use of the dominant-valency and the dominant-constituent rules are recommended by the IMA−CNMNC, it is worthwhile to analyse their basic aspects, here identified as follows: (1) the principle of the formula electroneutrality; and (2) the definition of an end-member formula (Hawthorne, 2002) that includes at most one site with double occupancy (i.e. heterovalent pair of ions or ion–vacancy pair). In addition, the concepts of total charge and charge constraint at the crystallographic sites should be considered. The charge constraint can be defined as an integer number close (or next) to the observed site total charge (STC). It provides information on possible root-charge and atomic arrangements; if such arrangements satisfy all the criteria of an end-member formula, the mineral may be identified.

Again, considering the composition ^[8](Ca_0.4Na_0.35K_0.25)^[4](Al_1.4Si_2.6)O₈, the key aspect is to explore the STC at the [8]- and [4]-fold coordinated sites: ^[8]STC = +1.4 and ^[4]STC = +14.6. As the former is close to +1 and the latter is close to +15, the charge constraints (+1 and +15) indicate that the mineral species may be consistent with the end-member root-charge arrangement (R ⁺)^Σ1+(R ³⁺R ⁴⁺₃)^Σ15+O₈, rather than (R ²⁺)^Σ2+(R ³⁺₂R ⁴⁺₂)^Σ14+O₈. In terms of atoms per formula unit (apfu), the atomic arrangement 0.60[(Na,K)(AlSi₃)] (= 3.00 apfu, limited by Na + K content) is larger than 0.40[(Ca)(Al₂Si₂)] (= 2.00 apfu, limited by Ca content). Thus, in accord with the dominant-constituent rule, Na_0.35 > K_0.25, the species corresponds to albite.

Note that the site total charge and charge constraint are another important way to manifest the dominant-valency rule in which the STC is used to identify the dominant root-charge arrangement consistent with an end-member formula.

Extension of the dominant-valency rule

For complex mineral compositions, it may appear that the simple application of the dominant-valency rule does not lead to a charge-balanced end-member formula. This is due to the occurrence of heterovalent substitution mechanisms at more than one crystallographic site (or group of sites). Starting from the albite composition ^[8](Na_0.60Ca_0.40)^[4](Al_1.40Si_2.60)O₈, we could assume a hypothetical heterovalent substitution mechanism affecting the larger cation site: 0.12 ^[8](Pb²⁺ + □) → 0.12 ^[8](Na⁺ + Na⁺). This substitution will lead to the composition ^[8](Na_0.36Pb²⁺_0.12□_0.12Ca²⁺_0.40)^[4](Al_1.40Si_2.60)O₈, which has 0.52 divalent (R ²⁺) apfu; the simple application of the dominant-valency rule thus leads to the unbalanced charge formula (CaAlSi₃O₈)^Σ1+. Application of the site-total-charge approach to this composition indicates +1.4 charges at the [8]-fold coordinated site, close to +1, thus confirming that the root-charge arrangements with total charge +1 are dominant at that site: in fact, [0.36(R ⁺) + 0.24(R ²⁺_0.5□_0.5)^Σ1+] = 0.60 apfu is larger than the largest amount of charge arrangement entirely composed by R ²⁺ cations = 0.52 apfu. In other words, the aggregate-charge arrangement [(R ¹⁺) + (R ²⁺_0.5□_0.5)^Σ1+] is more abundant than the largest amount of (R ²⁺) we can calculate from the mineral composition. As the arrangement (R ⁺_0.36) (limited by the Na content) is larger than (R ²⁺_0.12□_0.12)_Σ0.24 (limited by the number of vacancies), the relative dominant cation arrangement is given by ^[8](Na⁺), which leads to the end-member formula NaAlSi₃O₈. Figure 2 shows the boundaries between generalised mineral species in such a complex system involving a heterovalent substitution at two sites (Fig. 2a), followed by a heterovalent substitution at a single site (Fig. 2b).

Fig. 2. Schematic representations of coupled heterovalent substitutions at two sites (a), followed by a heterovalent substitution at a single site (b) leading to the site-total-charge approach.

Hatert and Burke (2008) have in fact addressed the cases of (1) coupled heterovalent substitutions at a single site; (2) heterovalent substitutions at two sites; and (3) heterovalent substitutions at two sites plus homovalent substitution at a single site, but have not considered the case (4) of coupled heterovalent substitutions at two sites along with the heterovalent substitution at a single site. This more complex case is now clarified (Fig. 2).

The jervisite example

The application of the site-total-charge approach should be used when the simple application of the dominant-valency rule leads to an unbalanced end-member formula. Let us consider the empirical formula of the jervisite pyroxene of Mellini et al. (1982):

$$ {^{M {\left( 2 \right)}} \left({\rm N}{\rm a}^ + _{0.43} {\rm C}{\rm a}^{2 + }_{0.31} {\rm F}{\rm e}^{2 + }_{0.14} \squ_{0.12}\right) _{\Sigma 1.00}} {^{M{(1)}}\left({{\rm S}{\rm c}^{3 + }_{0.66} {\rm M}{\rm g}^{2 + }_{0.19} {\rm F}{\rm e}^{2 + }_{0.15} }\right)}_{\Sigma 1.00} {\rm Si}_2{\rm O}_6, $$

in which divalent cations seem to predominate at the M(2) site with Ca²⁺ as dominant constituent, and trivalent cation predominate at the M(1) site with Sc³⁺. As a result, the simple application of the dominant-valency rule yields (^M(2)Ca^M(1)ScSi₂O₆)^Σ1+, which is not charge-balanced. However, the STC at M(2) (= +1.33) and M(1) (= +2.66) indicate the following charge constraints: (i) M(2)^Σ1+ compatible with both ^M(2)(R ⁺) and ^M(2)(R ²⁺_0.5□_0.5)^Σ1+; (ii) M(1)^Σ3+ compatible with R ³⁺ (Fig. 3). As a result, the root-charge arrangements consistent with an end-member are ^M(2)(R ⁺)^M(1)(R ³⁺)Si₂O₆ and ^M(2)(R ²⁺_0.5□_0.5)^M(1)(R ³⁺)Si₂O₆, which are related by the heterovalent substitution ^M(2)(Na⁺) ↔ ^M(2)(R ²⁺_0.5 + □_0.5). Regarding the dominant charge arrangements, ^M(2)[(R ⁺) + (R ²⁺_0.5□_0.5)^Σ1+] prevails over the divalent ^M(2)(R ²⁺) in terms of apfu: the sum of the charge arrangements with total charge +1 at the M(2) site, 0.43 apfu of ^M(2)(R ⁺) (limited by Na contents) and 0.24 apfu of ^M(2)(R ²⁺_0.5□_0.5)^Σ1+ (limited by the number of vacancies), yields an aggregate-charge arrangement ^M(2)[0.43(R ⁺) + 0.24(R ²⁺_0.5□_0.5)^Σ1+] equal to 0.67 apfu. The latter is even larger than the largest amounts of charge arrangement characterised by the sole occurrence of ^M(2)(R ²⁺), 0.45 apfu. Note that ^M(2)(R ²⁺_0.45) is a hypothetical value that we can calculate to compare with the dominant-charge arrangements: in fact, the occurrence of 0.24(R ²⁺_0.5□_0.5) will actually reduce ^M(2)(R ²⁺) to 0.33 apfu. Between the two root-charge arrangements characterised by a total charge +1 at M(2), 0.43[^M(2)(R ⁺)^M(1)(R ³⁺)R ⁴⁺₂O₆] is more abundant than 0.24[^M(2)(R ²⁺_0.5□_0.5)^M(1)(R ³⁺)R ⁴⁺₂O₆] and as the atomic arrangement 0.43[^M(2)(Na⁺)^M(1)(Sc³⁺)Si₂O₆] > 0.24[^M(2)(Ca²⁺_0.5□_0.5)^M(1)(Sc³⁺)Si₂O₆], the end-member formula is NaSc³⁺Si₂O₆.

Fig. 3. Schematic representations of site total charge and atomic charge arrangements at the M(2) (a) and M(1) (b) sites of jervisite (see text).

The reason why the dominant-valency rule apparently fails may be shown by the substitution mechanisms involving jervisite. In this regard, it is instructive to arrive at the jervisite empirical formula from the diopside composition CaMgSi₂O₆:

1. (1) the heterovalent substitution at two sites

   $$\eqalign{&\hskip-15pt ^{M {\left( 2 \right)}}\left( {{\rm N}{\rm a}^ + } \right)_{0.66} \,+\, ^{M{(1)}} \left( {{\rm S}{\rm c}^{3 + }} \right)_{0.66}\;\to\; ^{M{(2)}}\!\! \left( {{\rm C}{\rm a}^{2 + }} \right)_{0.66} \,+\, ^{M{(1)}} \left( {{\rm M}{\rm g}^{2 + }} \right)_{0.66} \cr & {\rm yield}{\rm s}\;^{M{(2)}} \left( {{\rm N}{\rm a}^ + _{0.66} {\rm C}{\rm a}^{2 + }_{0.34} } \right)\;^{M{(1)}} \left( {{\rm S}{\rm c}^{3 + }_{0.66} {\rm M}{\rm g}^{2 + }_{0.34} } \right){\rm S}{\rm i}_2{\rm O}_6;} $$

2. (2) the homovalent substitution at a single site

   $$\eqalign{& ^{M {\left( 1 \right)}}\left( {{\rm F}{\rm e}^{2 + }} \right)_{0.15}\; \to\; ^{M{(1)}}\!\! \left( {{\rm M}{\rm g}^{2 + }} \right)_{0.15} \cr & {\rm yield} {\rm s}\;^{M{(2)}} \left( {{\rm N}{\rm a}^ + _{0.66} {\rm C}{\rm a}^{2 + }_{0.34} } \right)\;^{M{(1)}} \left( {{\rm S}{\rm c}^{3 + }_{0.66} {\rm M}{\rm g}^{2 + }_{0.19} {\rm F}{\rm e}^{2 + }_{0.15} } \right){\rm S}{\rm i}_2{\rm O}_6;}$$

3. (3) the heterovalent substitution at a single site

   $$\eqalign{& ^{M {\left( 2 \right)}} \left( {{\rm F}{\rm e}^{2 + } + {\squ}} \right)_{0.12} \,\to\; ^{M{(2)}}\!\! \left( {2{\rm N}{\rm a}^ + } \right)_{0.12} \cr & \hskip-15pt {\rm yield}{\rm s}\;^{M{(2)}} \left( {{\rm N}{\rm a}^ {+} _{0.42} {\rm C}{\rm a}^{2 + }_{0.34} {\rm F}{\rm e}^{2 + }_{0.12} {\squ}_{0.12} } \right)^{M{(1)}} \left( {{\rm S}{\rm c}^{3 + }_{0.66} {\rm M}{\rm g}^{2 + }_{0.19} {\rm F}{\rm e}^{2 + }_{0.15} } \right){\rm S}{\rm i}_2{\rm O}_6,} $$
   which substantially corresponds to the empirical composition of jervisite.

The alluaudite example

The alluaudite supergroup contains phosphates and arsenates with the structural formula A(2)’A(1)M(1)M(2)₂(TO₄)₃; the cations are distributed mainly among four distinct crystallographic sites: the large cavities coordinated by the A(2)’ and A(1) sites in the channels of the structure, and the octahedrally-coordinated M(1) and M(2) sites. A wet chemical analysis of an alluaudite from the Buranga pegmatite, Rwanda, was published by Héreng (1989) and gives the following cation distribution:

$\eqalign { {^{A(2)^{\prime}}(\squ)^{A(1)} ({\rm Mn}^{2 + }_{0.34} {\rm Ca}^{2 + }_{0.17} {\rm Na}_{0.29} {\squ}_{0.21})_{\Sigma 1.00}} {^{M(1)}( {\rm Mn}^{2 + })} \cr {^{M(2)} ( {\rm Fe}^{3 + }_{1.70} {\rm Fe}^{2 + }_{0.15} {\rm Mn}^{2 + }_{0.10} {\rm Mg}_{0.04}{\rm Zn}_{0.01} )_{\Sigma 2.00}} {^{T} ( {\rm PO}_4 )_3}.}$

In this formula, vacancies are dominant at A(2)’, divalent cations with Mn²⁺ > Ca at A(1), Mn²⁺ at M(1) and Fe³⁺ at M(2), thus leading to the unbalanced end-member formula [□Mn²⁺Mn²⁺Fe³⁺₂(PO₄)₃]^Σ1+. The dominant-valency rule cannot be simply applied to the A(1) site population, due to the occurrence of the heterovalent substitution ^A(1)(R ²⁺ + □) → ^A(1)(2Na⁺) which produces a decrease of the Na content and an increase of the R ²⁺-cations and vacancies at the A(1) site. However, this substitution mechanism preserves the STC, whose value (+1.31) is close to +1. In fact, the alluaudite structure is dominated by the aggregate-charge arrangement ^A(1)[(R ²⁺_0.5□_0.5)^Σ1+ + (R ⁺)]: the sum of ^A(1)(R ²⁺_0.21 + □_0.21) (Σ = 0.42 apfu, limited by the number of vacancies) plus ^A(1)(R ⁺_0.29) (= 0.29 apfu, limited by Na contents) is equal to 0.71 apfu; the latter is larger than the largest amount of charge arrangement calculated using only R ²⁺-cations at A(1): 0.51 apfu. Looking at the dominant aggregate-charge arrangement with total charge +1, ^A(1)(R ²⁺_0.21□_0.21)_Σ0.42 > ^A(1)(R ⁺_0.29). In accord with the dominant-constituent rule, ^A(1)Mn²⁺ > ^A(1)Ca²⁺, the relative dominant atomic arrangement at the A(1) site is hence (Mn²⁺_0.5□_0.5)^Σ1+ and the end-member formula is □(Mn²⁺_0.5□_0.5)Mn²⁺Fe³⁺₂(PO₄)₃. It should be noted that the heterovalent-pair ^A(1)(R ²⁺_0.5□_0.5)^Σ1+ and the homovalent ^A(1)(R ⁺) play the same role in the charge balance (overall electroneutrality).

The garnet example

The approved garnet nomenclature is based on the dominant-valency rule, but this rule was unsuccessful in discriminating schorlomite from morimotoite/andradite. Let us consider the schorlomite composition from the type locality Magnet Cove, Arkansas (Grew et al., 2013): ^X[(Ca²⁺_2.907Fe²⁺_0.043Mn²⁺_0.035)Na⁺_0.015]_Σ3.000^Y[(Ti⁴⁺_1.069Zr⁴⁺_0.055)Fe³⁺_0.517(Fe²⁺_0.204Mg²⁺_0.155)]_Σ2.000^Z[Si⁴⁺_2.250(Fe³⁺_0.588Al³⁺_0.162)]_Σ3.000O₁₂ in which the dominant valence at the X site is +2, and at the Y and Z sites is +4. The simple application of the dominant-constituent rule fails as the dominant constituents ^XCa²⁺, ^YTi⁴⁺ and ^TSi⁴⁺ lead to unbalanced end-member formula (Ca²⁺₃Ti⁴⁺₂Si⁴⁺₃O^2–₁₂)^Σ2+. This issue was overcome by Grew et al. (2013) by using the most abundant end-member composition: schorlomite Ca₃Ti₂(SiFe³⁺₂)O₁₂ (37.5%) > morimotoite Ca₃(TiFe²⁺)Si₃O₁₂ (35.9%) > andradite Ca₃(Fe³⁺₂)Si₃O₁₂ (25.9%). This is equivalent to stating the schorlomite-group minerals (which include the mineral species hutcheonite, irinarassite, kerimasite, kimzeyite, schorlomite and toturite) are identified by the dominant-end-member approach.

With regard to the substitution types involved in the empirical formula of this garnet, starting from andradite Ca₃(Fe³⁺₂)Si₃O₁₂, we have a heterovalent substitution at two sites (schorlomite → andradite substitution type):

$$^Y {\rm T}{\rm i}^{4 + }_{0.75} \,+\; ^Z\!\!{\rm F}{\rm e}^{3 + }_{0.75} \to ^Y\!\!{\rm F}{\rm e}^{3 + }_{0.75} \,+\; _{}^Z\!\! {\rm S}{\rm i}^{4 + }_{0.75} $$

yielding the formula Ca₃^Y(Ti⁴⁺_0.75Fe³⁺_1.25)_Σ2.00^Z(Si_2.25Fe³⁺_0.75)_Σ3.00O₁₂, plus a heterovalent substitution at a single site (morimotoite → andradite substitution type):

$$^Y \left( {{\rm T}{\rm i}^{4 + }_{0.38} + {\rm F}{\rm e}^{2 + }_{0.38} } \right) \to 2^Y\left( {{\rm F}{\rm e}^{3 + }} \right)_{0.38}$$

yielding the formula Ca₃^Y(Ti⁴⁺_1.13Fe³⁺_0.49Fe²⁺_0.38)_Σ2.00^Z(Si_2.25Fe³⁺_0.75)_Σ3.00O₁₂, which reasonably corresponds to the empirical one, with Ca = ^X(Ca²⁺+ Fe²⁺+ Mn²⁺), ^YTi⁴⁺ = ^Y(Ti⁴⁺+ Zr⁴⁺), ^YFe²⁺ = ^Y(Fe²⁺+ Mg²⁺) and ^ZFe³⁺ = ^Z(Fe³⁺+ Al³⁺). Similarly to the jervisite example above, the garnet from Magnet Cove can also be identified by the dominant-valency rule using the concepts of STC and charge constraint to select the possible root-charge and atomic arrangements among the end-members ^X(Ca₃)^Σ6+ Y(Ti₂)^Σ8+ Z(SiFe³⁺₂)^Σ10+O₁₂ (schorlomite), ^X(Ca₃)^Σ6+ Y(Fe³⁺₂)^Σ6+ Z(Si₃)^Σ12+O₁₂ (andradite) and ^X(Ca₃)^Σ6+ Y(TiFe²⁺)^Σ6+ Z(Si₃)^Σ12+O₁₂ (morimotoite). In detail: the total charge at X (= +5.99) is very close to +6, at Y (= +6.77) is closer to +6 than +8, and at Z (= +11.25) is closer to +12 than +10; note that the charge constraint Y ^Σ7+ and Z ^Σ11+ are ruled out as leading to a formula, (Ca₃)^Y(TiFe³⁺)^Z(Si₂Fe³⁺)O₁₂, inconsistent with the end-member definition (Hawthorne, 2002); the charge constraints (X ^Σ6+, Y ^Σ6+ and Z ^Σ12+) are only compatible with the root-charge arrangements ^X(R ²⁺₃)^{Σ6+ Y}(R ⁴⁺R ²⁺)^{Σ6+ Z}(R ⁴⁺₃)^Σ12+O₁₂ (morimotoite type) and ^X(R ²⁺₃)^{Σ6+ Y}(R ³⁺₂)^{Σ6+ Z}(R ⁴⁺₃)^Σ12+O₁₂ (andradite type), but not with the arrangement ^X(R ²⁺₃)^Σ6+ Y(R ⁴⁺₂)^Σ8+ Z(R ⁴⁺R ³⁺₂)^Σ10+O₁₂ (schorlomite type) that can be considered as a minor component; in this regard, note that amount of the aggregate-charge arrangement at Y with total charge +6, ^Y[0.718(R ⁴⁺_0.5R ²⁺_0.5) + 0.517(R ³⁺)] = 1.235 apfu, is larger than the largest amount of charge arrangement characterised solely by the ^YR ⁴⁺-cations (1.124 apfu); as ^Y(R ⁴⁺_0.5R ²⁺_0.5)_0.718 > ^Y(R ³⁺)_0.517, the relative dominant charge arrangement is ^Y(R ⁴⁺_0.5R ²⁺_0.5); in terms of constituents, it corresponds to ^Y[Ti⁴⁺_0.5(Fe²⁺,Mg²⁺)_0.5], which in accord with the dominant-constituent rule, ^Y(Fe²⁺_0.204) > ^Y(Mg²⁺_0.155), leads to ^Y(Ti⁴⁺_0.5Fe²⁺_0.5); therefore, the garnet species from Magnet Cove corresponds to morimotoite, even though the most abundant end-member component is schorlomite (Grew et al., 2013).

It is worth noting that this garnet example showed that the STC at Y (= +6.77) and Z (= +11.25) were very close to +7 and +11, but we selected the integer numbers +6 and +12, respectively, as the choice of charge constraints Y ^Σ7+ and Z ^Σ11+ would lead to the formula ^X(Ca₃)^Y(TiFe³⁺)^Z(Si₂Fe³⁺)O₁₂ with double occupancy of two sites. As a rule, if the integer number closest to the STC is not consistent with an end-member, another integer number in line with the end-member definition must be selected. The incorrect integer number can be recognised as it results in root-charge and atomic arrangements leading to a formula with double occupancy of two sites or charge imbalance.

The detailed procedure reported above for garnet can be summarised as follows:

1. (1) The STC at X (+5.99), Y (+6.77) and Z (+11.25) indicate the charge constraints X ^Σ6+, Y ^Σ6+ and Z ^Σ12+.

2. (2) These constraints lead to the possible root-charge arrangements ^X(R ²⁺₃)^{Σ6+ Y}(R ⁴⁺R ²⁺)^{Σ6+ Z}(R ⁴⁺₃)^Σ12+O₁₂ and ^X(R ²⁺₃)^{Σ6+ Y}(R ³⁺₂)^{Σ6+ Z}(R ⁴⁺₃)^Σ12+O₁₂, which are end-members.

3. (3) As the condition of the charge balance in end-members is satisfied, we can calculate the amounts of root-charge and atomic arrangements in terms of apfu: ^XR ²⁺ ≅ Ca, ^ZR ⁴⁺ = Si and as ^Y(R ⁴⁺_0.5R ²⁺_0.5)_0.718 > ^Y(R ³⁺)_0.517 leads to ^Y[Ti⁴⁺_0.5(Fe²⁺,Mg²⁺)_0.5] in which ^Y(Fe²⁺)_0.204 > ^Y(Mg²⁺)_0.155 leads to the end-member Ca₃(TiFe²⁺)Si₃O₁₂.

The dominant-valency rule is able to identify this garnet if the concepts of site total charges and charge constraints, dictated by the mineral composition and the electroneutrality principle, are taken into account. These concepts emphasise the role of the root-charge arrangements compatible with the site populations and the end-member definition. The dominant-constituent rule can hence be applied to the relative dominant root-charge arrangement.

The aforementioned concepts are also reflected in the ternary composition diagrams. Morimotoite/andradite and schorlomite are related by coupled heterovalent substitutions at the Y and Z sites, whereas morimotoite and andradite are related by a coupled heterovalent substitutions at the Y site. Plotting the compositions of the Y site in a triangular diagram with (R ⁴⁺)^Σ4+, (R ⁴⁺_0.5+R ²⁺_0.5)^Σ3+ and (R ³⁺)^Σ3+ placed at each corner, the boundaries crossing at the centre of the diagram are displaced as follows: 25% for the component (R ⁴⁺)^Σ4+, 37.5% for both (R ⁴⁺_0.5+R ²⁺_0.5)^Σ3+ and (R ³⁺)^Σ3+ (Fig. 4). This displacement is dictated by the different charge or cation arrangements at the Z site between morimotoite/andradite and schorlomite: ^Z(Si⁴⁺₃)^Σ12+ and ^Z(Si⁴⁺R ³⁺₂)^Σ10+, respectively. As a result, Fig. 4 may be used to discriminate the schorlomite-group minerals from the ‘Ca-garnet-group minerals’ in line with the dominant-valency rule (cf. Fig. 4 of this study with fig. 7 of Grew et al., 2013) as well as with the current garnet nomenclature (the first criteria for distinguishing the group in garnets are the total charge at the Z site and symmetry). A similar argumentation should be applied to the ternary diagram andradite–morimotoite–menzerite-(Y), where the boundaries between the species are redefined in Fig. 5.

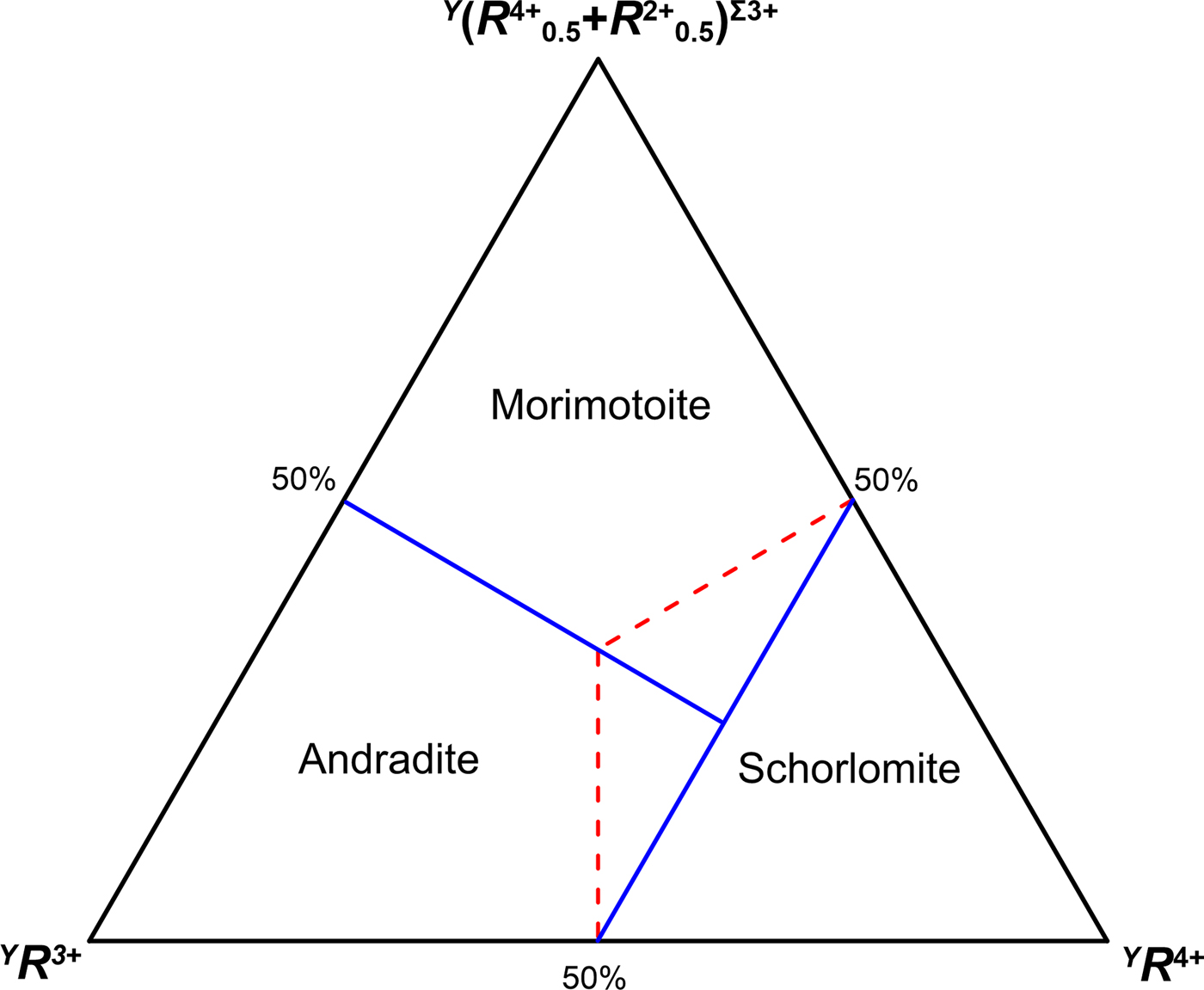
Fig. 4. Diagram for discriminating the species in the schorlomite−andradite−morimotoite system: solid blue lines are consistent with the dominant-valency rule, whereas dashed red lines are consistent with the dominant-end-member approach (cf. with fig. 7 of Grew et al., 2013).

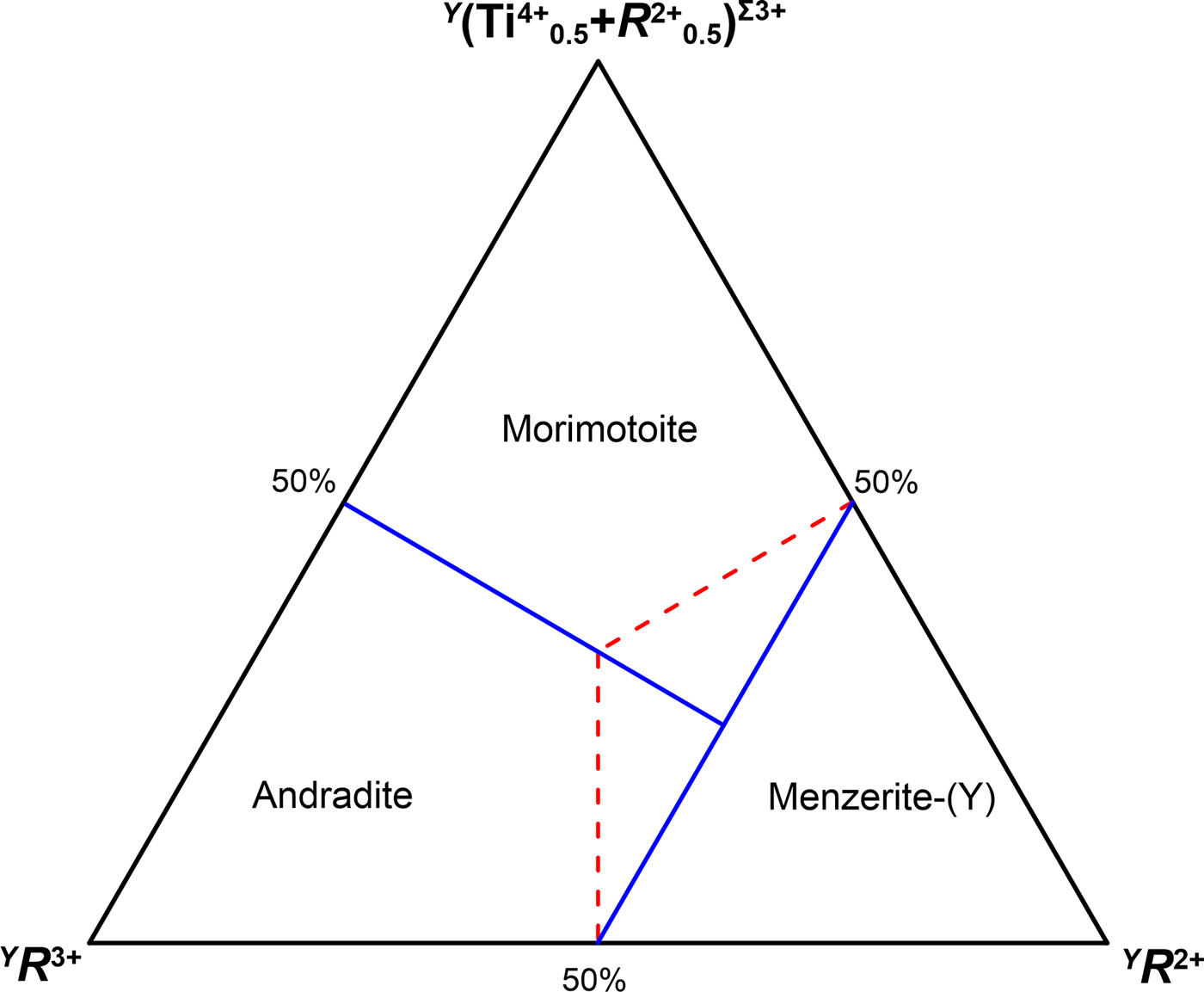
Fig. 5. Diagram for discriminating menzerite-(Y) from andradite and morimotoite: solid blue lines are consistent with the dominant-valency rule, whereas dashed red lines are consistent with the dominant-end-member approach (cf. with fig. 10 of Grew et al., 2013).

Conclusions

Even if no new nomenclature rules have been introduced in the present paper, the following aspects were discussed with the aim to improve and clarify the application of the dominant-valency rule in mineral nomenclature.

– An end-member formula should always be derived from a mineral composition and it should be consistent with the dominant atomic arrangement of the dominant root-charge arrangement.

– The dominant-valency rule and the dominant-end-member approach may not always converge to the same mineral species.

– The IMA−CNMNC recommends using the dominant-valency rule because it alone may lead to unambiguous mineral identification.

– When the simple application of the dominant-valency rule does not give charge-balanced end-member formulae, it may be useful to use the site-total-charge approach to identify the most appropriated integer number (charge constraint) corresponding to dominant root-charge and atomic arrangements consistent with the end-member formula definition.

The goal of mineral nomenclature should be the identification of the mineral end-member formula (and polymorphic forms). This overriding condition can be achieved by using the dominant-valency rule and/or the site-total-charge approach. Consequently, both procedures should be considered complementary to each other for mineral identification. We cannot exclude the possibility that these procedures will not apply to some mineral compositions, but they may provide the basis to improve our future understanding of mineral systems. The direct consequences of the modifications, here recommended, are a redefinition of the boundaries between garnet species andradite, morimotoite, schorlomite, and menzerite-(Y). As stated by Hatert and Burke (2008), these guidelines do not apply automatically to existing mineral species, and any modification of the current nomenclature should be submitted to the IMA−CNMNC for approval.