Introduction
Materials informatics is the application of informatics (the study of the structure and properties from scientific information) to materials science and engineering to aid in the understanding, development, and discovery of materials. Much of the initial emphasis in materials informatics has been placed on parametric first-principles exploration of lattice structures of stable multicomponent compounds and phases, or small-to-moderate-scale molecular structures that may deliver desired functionality. Reference Rajan1,Reference Kalidindi and De Graef2 Typically, this involves scripting workflows to systematically explore a range of material compositions and resulting energy-minimized structures using density functional theory, molecular statics, or some other scheme built upon ground-state stability. Another approach, consistent with bioinformatics applications, is to introduce high-throughput synthesis of structure, followed by rapid and approximate property assessment in experimental assays. With such machinery in place, regardless of the blend of computation and experiments, an essential prong to this strategy is the application of data science to explore, screen, and select potential materials systems to meet application requirements. These methods constitute what may be regarded as the discovery thrust of materials informatics.
For example, consider the use of informatics in materials discovery through the prediction of phase stability in alloys as a function of their constituents. Electronic-structure calculations are being used to calculate the energetics of alloyed systems using computational combinatorics. Reference Jain, Ong, Hautier, Chen, Richards, Dacek, Cholia, Gunter, Skinner, Ceder and Persson3,Reference Ceder and Persson4 From these data sets, one can determine optimal configurations and the properties specific to those structures, including elastic constants. Reference de Jong, Chen, Angsten, Jain, Notestine, Gamst, Sluiter, Ande, van der Zwaag, Plata, Toher, Curtarolo, Ceder, Persson and Asta5 The Materials Project at Lawrence Berkeley National Laboratory provides results of such calculations as a web service. 6
Most practical materials systems, however, consist of interfaces that demarcate grain or phase boundaries, which influence thermal, mechanical, and physical properties at the mesoscale. For example, structural materials have a rich history of reliance on structure hierarchy well above the scale of the elementary unit cell of the lattice to achieve superior performance. The scales of structure in alloys range from several nanometers for optimal precipitate strengthening, to tens of nanometers for multilayers and nanotwins, to hundreds of nanometers for distributed coherent precipitates and second phases, to tens of micrometers for grain-size distributions.
Figure 1 Reference McDowell7,Reference McDowell, Panchal, Choi, Seepersad, Allen and Mistree8 shows an example of scales of material structure hierarchy that control properties of precipitate-strengthened Ni-base superalloys for aircraft gas-turbine engine hot section components, such as the disks, which turn under the influence of the hot gases leaving the combustor. Composite materials derive their outstanding properties from the scale hierarchy associated with spatial distribution of phases with strong property contrast, in addition to interphase regions that modify phase interactions. Properties of structural materials are mediated by point, line, and surface defects, with the latter two types having extended character and both short- and long-range structure.
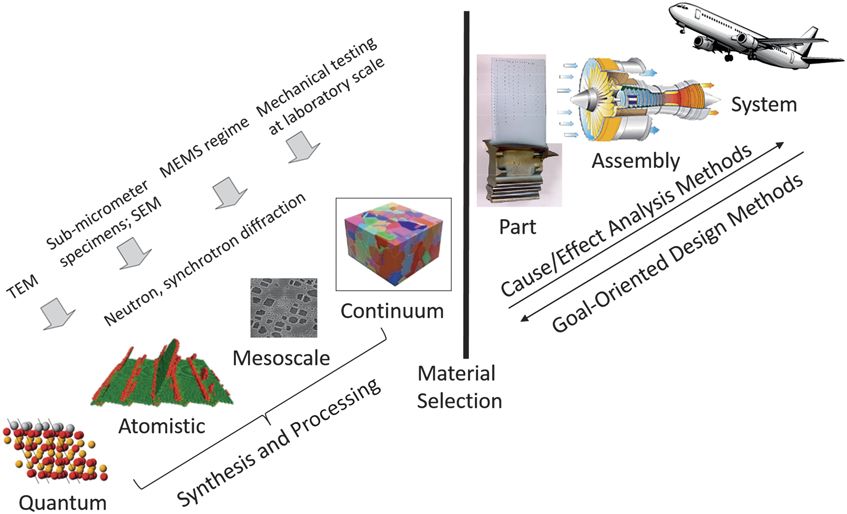
Figure 1. Illustration of the role of microstructure hierarchy in Ni-base superalloys, ranging from lattice structures (first principles), to defect mediation at matrix–precipitate interfaces (atomistics), to mesoscale many-body interactions of dislocations with precipitates (discrete dislocation and phase-field simulations), to polycrystalline structures (continuum finite element or finite difference methods). Achieving greater concurrency of top-down design of engineering systems with materials development through this hierarchy of structure is an important objective, effectively supplanting materials selection as the dominant interface to materials research and development. Adapted with permission from References Reference McDowell7 and Reference McDowell, Panchal, Choi, Seepersad, Allen and Mistree8. © 2010 Springer and 2010 Oxford University Press, respectively. Note: TEM, transmission electron microscopy; SEM, scanning electron microscopy; MEMS, microelectromechanical systems.
The application of data science and informatics methods to microstructures has not been strongly emphasized in the solid-state physics, chemistry, and materials science communities until recently. There are many challenges in applying informatics methods to microstructures that arise from the complexity of their hierarchical structures. The benefits of applying these methods to microstructures, however, are great, given their common characteristic of metastability and their important role in determining structure–property relations. The situation is further complicated by the presence of phase and structural transitions, which may yield disruptive advances in available properties. For example, transformation toughening confers both workability and toughness.
Metastability of structural materials is a natural byproduct of nonequilibrium thermomechanical processing and associated structure evolution, which gives rise to novel, tailored microstructures. Achieving such hierarchical structures has historically been more art than science, as the ability to apply predictive computational models has been limited in this regard. Recent advances in phase-field modeling and other related methods Reference Steinbach9,Reference Chen10 offer promise in that they (1) clearly distinguish nucleation and growth phenomena; and (2) consider thermodynamics in terms of stable phases, interfaces, and driving forces for kinetics. These are essential elements of a strategy for modeling process–structure relations for hierarchical microstructures, since the time scales for equilibration at a given temperature vary according to the scale of each structure. The ability to computationally predict the emergent, collective properties/responses of interest for these hierarchical structures has been elusive, resulting in an emphasis on experimental protocols.
Multiscale modeling methods meanwhile are steadily advancing, in conjunction with experimental measurements, with fidelity appropriate to various levels of hierarchy to confirm mechanisms and validate models. Reference van Beers, Kouznetsove, Beers, Tschopp and McDowell11,Reference Pollock and LeSar12 They have received investment now for nearly 20 years. Still, it seems clear that the pathway to truly predictive multiscale models for process–structure and structure–property relations is a long and winding one. Much of the behavior of materials is complicated by the presence of complex hierarchical structures that manifest themselves in physical responses over a wide range of length and time scales, Reference Ashby13 as indicated in Figure 1. Structure–property relations for metal alloys, for example, while fundamentally governed by the crystal structure, are highly dependent on the distributions of defects at the mesoscale. These defects can include grain boundaries in a polycrystalline material, dislocations whose generation, annihilation, interactions, and motion govern yield and work hardening, point defects critical to solid-solution strengthening, and diffusion. This collection of structures over a range of hierarchical scales is generally referred to as a material’s microstructure.
The role of data science and informatics combined with digital representation of structure hierarchy is not only scientifically interesting, but also practically compelling as a means to bridge these gaps in a reasonable timeframe to complement multiscale modeling and high-throughput experimental methods. This leads to an operative definition of the theme topic of this issue, Microstructure Informatics, as a branch of materials data science and informatics concerned with the identification and quantification of dominant scales of hierarchy of structure that can be characterized, digitally rendered, and systematically explored in terms of correlations that govern process–structure and structure–property relations.
Why is microstructure informatics important?
Major current technology thrusts, such as the Materials Genome Initiative 14 and Integrated Computational Materials Engineering, 15 have made the persuasive argument that the sequence of stages to develop and certify a new material are consistently too long (∼20 years) to achieve concurrency with the systems design process, alluded to in Figure 1. We have already mentioned the long-term prospect of realizing predictive multiscale methods for process–structure and structure–property relations of materials with hierarchical structure to support materials design and development. Although well established in certain fields, such as biology, weather forecasting, and climate change, methods rooted in data science have witnessed considerably less application in addressing process–structure–property (PSP) relations of materials. By taking advantage of prospects for enhanced decision support from computational modeling and simulation tools, higher resolution and more rapid characterization instruments and methods, and incorporating modern data science tools and methods, researchers have increasingly focused on the goal of accelerating the insertion of new or improved structural materials into next-generation transportation vehicles and propulsion systems.
Early demonstration projects such as the Defense Advanced Research Projects Agency Accelerated Insertion of Materials (AIM) Program Reference Apelian16 from 2000 to 2003 provided a basis for optimism in this regard. The AIM program was focused on metallic systems (Ni-base superalloys for gas-turbine engine disks) and composite airframe materials. In AIM, various experimental and computational aspects of material process–structure and structure–property relations were consolidated into a designer knowledge base Reference McDowell, Backman, Ghosh and Dimiduk17 to provide a means to minimize necessary iterations in the presence of uncertainty and converge on designed materials for specific components and performance requirements. Reference McDowell and Olson18
There are many ways to describe the microstructure of a material. These include standard metrics, such as the crystal structure, the mean grain size and shape, the orientation of the grains (the texture), and grain-boundary character distribution. We also include parameters that describe other defect distributions, including the structure of multiphase materials, porosity, and dislocation substructures. Each of these structures may influence the material properties. The goal of materials informatics is to use data to identify these effects and examine whether correlations exist between the various microstructural parameters and a material property of interest, including the degree of potential cross-coupling of these parameters in determining such a property (i.e., if two types of structures act in combination or can be considered as independent).
There are several challenges to quantifying microstructure. First, microstructures are typically quantified by assessing digital images from two-dimensional (2D) sections, which cannot appropriately capture the three-dimensional (3D) character of the structure. Second, hierarchical structures over a vast spatial range from a few nanometers to several hundred micrometers require different measurement resolutions and associated techniques, presenting challenges to combining information with proper spatiotemporal identification. Third, most of the metrics previously described are typically used to correlate with mean properties; on the other hand, minimum properties among a statistical distribution of properties are often of interest and depend on the distribution of structures, such as the grain size, across a material. Examples include minimum fatigue strength or fatigue life, minimum fracture toughness, and minimum ductility. Fourth, microstructure evolves as a function of temperature and with external loading stimuli, and the associated structures are metastable. In particular, point, line, and surface defects that are arranged to deliver desired performance in modern alloy systems evolve over time in service, greatly complicating the assessment of long-term durability and suitability for applications. This also fundamentally limits existing technologies for screening alloys based only on first-principles calculations, as alluded to in the foregoing.
Recently, much progress has been made in the 3D characterization of microstructures, as described in a series of recent articles. Reference Thornton and Poulsen19 One promising approach employs serial sectioning combined with optical microscopy and electron backscatter diffraction to yield 3D microstructures represented with voxels. Reference Lewis and Geltmacher20,Reference Lewis, Suh, Stukowski, Geltmacher, Spanos and Rajan21 Advances in using synchrotron radiation have enabled nondestructive characterization of 3D microstructures and hint at multiresolution techniques to augment optical microscopy (see the June 2016 MRS Bulletin issue: “Synchrotron radiation research in materials science”). Reference Pokhatel, Lind, Kanjarala, Lebensohn, Li, Kenesei, Suter and Rollett22 From these data, one can quantify the distribution of structures across a fully 3D microstructure, from which various statistics, such as mean, standard deviation, and even higher-order statistical moments of the spatial distribution, can be determined.
Microstructure informatics approaches
While offering substantial improvement relative to that available from simple 2D data sets, employing brute-force statistical analyses of 3D structures to identify spatial correlations between various elements of a microstructure is challenging. A new monograph on microstructure informatics by Kalidindi Reference Kalidindi23 focuses on developing mathematical correlations between microstructural features and properties or responses of interest. In their article in this issue, Kalidindi et al. discuss the need for an e-collaboration infrastructure in which distributed team members with different tools and expertise can share data, capabilities, ideas, and intermediate results to accelerate the identification of the most efficient and profitable “pathways” for data to flow and for models or data analytics to be executed to provide decision support in materials development. These pathways or “workflows” can then serve as templates for user interactions and schema to similarly support various other analogous materials-development problems.
Problems of interest to microstructure informatics chiefly focus on the relation of a hierarchy of material structure to properties or responses at various length and time scales. Two case studies are presented, one comprising a model-based study that relies on machine learning to pursue computational design and development of Ni-base superalloys. The second case study focuses on a rigorous framework for the stochastic quantification of the material structure, based on well-established concepts of n-point spatial correlations (often simply referred to as n-point statistics) that provide a set of measures organized by increasing amounts of information. This type of framework furnishes a fairly general description of the microstructure and is not limited to any specific length or time scale. It provides a number of advantages. One is its ability to represent the microstructure mathematically using two-point statistics, typically, or three-point and higher order as necessary. Building on the statistical continuum theory of Kröner, Reference Kröner, Kanninen, Adler, Rosenfeld and Jaffee24,Reference Kröner25 it is then possible to describe correlations between microstructure distributions and material responses of interest at the scale of a representative volume element (RVE) by first calibrating to simple microstructures and then extending to microstructures of arbitrary complexity composed of the same set of objects, for example, phases or defects. The RVE is the smallest volume that is statistically representative of the overall microstructure with regard to a given property or response.
In this way, a series expansion can be written to represent structure–property relationships, decomposing each term according to a microstructure function and an influence function for spatial correlations of structure-response functions of appropriate order (influence functions describe how changing one point of the sample affects an estimator [e.g., a correlation function, as an approximation of a Green’s function]). These influence functions are calibrated either to experiments or more typically to high-fidelity RVE simulations. Principal component analysis can be exercised to identify a key, limited set of terms that contain most of the relevant correlations in structure–property relations, lending considerable efficiency to exploration of the microstructure design space.
Another article in this issue describes a different, complementary approach to using informatics to link the process route with microstructure and microstructure with properties, achieving so-called PSP linkages. In their article, Wodo et al. point to the lack of a unified mathematical formalism to seamlessly connect chemistry with thermodynamics and kinetics to inform PSP linkages via a predictive design strategy. To fill this gap, they introduce microstructure informatics as a means to capture the interaction between processing variables and their influence on chemistry–microstructure–property correlations via use of manifold representations and data-compression methods to achieve substantial reduction of model order, facilitated by principal component analyses. The gist of this approach is to reduce the space of microstructure descriptors to a set of meaningful descriptors that manifest correlations. Examples are provided for establishing libraries of properties to support grain-boundary engineering and the design and optimal fabrication of organic solar cells.
They close with a discussion of the need for high-performance computing to address the “big data” aspects of PSP linkages via microstructure informatics for problems involving complex PSP relations, for which the “phase space” to explore in correlations is high dimensional. Such problems are commonplace in designing engineering materials, which previously has been a largely empirical, iterative, and time-consuming exercise. The authors point to the need for approaches that allow materials developers and design engineers to explore PSP relations without requiring high-level domain expertise in software engineering, fault tolerance, and high-performance computing, and advocate a cloud-computing paradigm. We add to their stipulations the need for uncertainty quantification and the management of uncertainty margins in the entire enterprise of pursuing PSP linkages.
Multiscale modeling
One of the grand challenges for computational materials science is the extreme range of length and time scales that govern material behavior, ranging from the angstrom length and sub-picosecond time scales of atomic-scale behavior to the respective length and time scales of meters and years for material behavior in engineering applications. At each scale of microstructure, there is a structural “unit” that dominates the physical processes at that scale. These units are the entities whose dynamics define the physics of interest at each scale. Typically, a set of models of materials behavior is created for each of the various scales. Reference LeSar26
The coupling of microstructure informatics with multiscale modeling and simulation offers an opportunity to significantly leverage multiscale modeling to provide decision support for materials development and to establish statistical confidence in structure–property relations. Improved fidelity and accuracy of multiscale models to predict structure-dependent behavior can, in turn, cooperate and interplay with microstructure informatics to improve overall confidence levels for estimates of structure–property relations, thereby reducing the burden on costly and time-consuming experimental protocols. The past few decades have witnessed important trends in multiscale modeling that cut across disciplines. In particular, first principles, atomistics, and Monte Carlo methods that originated in computational physics and chemistry have now become commonplace in engineering curricula and research, with materials science and engineering serving as a bridge in the materials context. Reference LeSar26,27 Moreover, there is an increased interest in finite element methods, continuum mechanics, and constitutive modeling from the condensed-matter physics and chemistry/chemical engineering communities. There has been a remarkable transformation in engineering sciences and computational mechanics of materials to embrace lower scale phenomena and insert related information into higher scale models.
In the most common view of multiscale materials modeling, a hierarchy of models and simulations, each describing a specific scale and its associated phenomena, is linked to create a multiscale description of materials behavior with information (e.g., outputs from one model as inputs to the next) being passed sequentially from scale to scale, an approach that is often referred to as information passing or sequential, hierarchical multiscale modeling. Reference Fish28 Inherent in the information-passing paradigm is the lack of corresponding inverse models that would allow us to predict the needed structures and properties at the small scale from desired properties or responses at a larger scale—information flows only in one direction, from small scales to large.
Another approach, which is often referred to as concurrent multiscale modeling, 27 links simulations at different length and time scales directly within a single integrated framework. Its development has been substantially more limited than that of hierarchical multiscale modeling. This approach has the advantage of enabling the flow of information between scales, both bottom-up and top-down. This can facilitate prediction of localization of damage and deformation at notches, for example, while simultaneously considering overall component-level response. Reference Ghosh29–Reference Fernery and Kabiri31 As in sequential multiscale simulations, models must be developed and applied at multiple scales, with the added complication of determining appropriate interfaces between the models that enable them to be used concurrently. This also introduces new sources of uncertainty related to the idealizations and approximations in strong coupling of models at different length and time scales.
A form of concurrent multiscale modeling, termed domain decomposition, focuses on modeling material response at distinct resolutions in different spatial domains, for example, using atomistic resolution near grain boundaries and continuum dislocation dynamics Reference Shilkrot, Curtin and Miller32,Reference Shilkrot, Miller and Curtin33 or coarse-grained atomistic approaches Reference Shenoy, Miller, Tadmor, Phillips and Ortiz34–Reference Xu, Che, Xiong, Chen and McDowell37 away from the these boundaries. The time scale of these domain decomposition methods is typically dictated by the most highly resolved description used in any region of the overall domain.
Methods for computational homogenization of microstructures have received considerable attention in the literature, in which a heterogeneous material is replaced by an equivalent homogeneous material at the RVE level, with the goal of computing its effective properties. This field has evolved considerably in the past few decades relative to previous generations of approaches that involved considerable idealization of microstructure and interfaces. More recent approaches exploit high-performance computing to consider realistic microstructures, interface behavior, and nonlinear and higher order responses of individual phases in solving nested initial boundary value problems at multiple scales.
The article by Geers and Yvonnet provides an overview of how the fields of computational materials science and mechanics of materials have essentially merged in the past decade, with a common purpose of modeling responses and properties of microstructures at various scales. In particular, they provide examples for copper-rubber interface delamination in stretchable electronics and advanced dislocation-based plasticity models. The fast Fourier transform method is discussed as a means to pursue much more efficient computational homogenization for 3D microstructures, including multiphysics problems. The article closes with a discussion of reducing computational costs in nonlinear coupled simulations at two scales (substructures and interfaces) in a composite material using parallel computing strategies, along with model-reduction techniques and approximate two-scale decoupling methods based on informatics learning strategies such as neural networks.
The homogenization strategies discussed by Geers and Yvonnet often seek to build “bottom-up” relations, most often using hierarchical and sometimes concurrent multiscale modeling strategies. On the other hand, it is clear that information must flow from top to bottom to pursue materials design to satisfy specified performance requirements. Pursuit of inverse-design problems requires top-down invertibility of PSP relations; for example, the relations developed via microstructure informatics Reference Kalidindi23 are often amenable to inversion. McDowell et al. Reference McDowell, Panchal, Choi, Seepersad, Allen and Mistree8 extensively discuss a more general methodology to conduct materials design exploration that is informed using various scale-specific tools (experiments, models, metamodels, and informatics correlations), whether hierarchical or concurrent in nature, and exploits concepts in the multidisciplinary design optimization community to evaluate PSP linkages as a multilevel design exercise in the presence of uncertainty.
A key goal of multiscale modeling is to provide decision support in multilevel design and development of materials in the presence of various sources of uncertainty, including randomness of the microstructure, the structure of the models, and values of model parameters. This includes providing support for understanding coupling for phenomena across length and time scales such that structure can be designed and controlled to manipulate properties/responses at a higher scale in an intended manner. It should be understood that multiscale modeling serves the purposes of multilevel design of materials with microstructure, but does not constitute materials design in its own right.
Digital microstructure representation and uncertainty quantification
The Michel and Meredig article focuses on how to digitally represent the vast amount of information necessary to express not only microstructure descriptors at length scales, but also all relevant information associated with PSP relations, ranging from atomic-scale structure, through various levels of hierarchy of microstructure, and onto the component design level. They contend that this must be pursued in a machine-readable, structured format to serve as input data for informatics schemes. They introduce a hierarchical data structure called physical information file (PIF) as a flexible schema to store process history, structure, properties, devices, and other subsystems of the physical system of interest in the coupled materials development and component design system.
However, databases that are too narrowly or rigidly structured cannot serve the necessary purposes of materials design via distributed collaboration because they are not sufficiently flexible for use by multiple developers, and hence do not incentivize widespread usage. Reference McDowell38 To this end, they provide simple examples to explain the flexibility of their PIF approach, including properties of LiNiO thermoelectrics and an ionic liquid. While these examples focus on structure at the atomic/molecular scale, they argue for generalization to incorporate more complex mesoscopic structures at higher length scales via nesting of system and subsystem objects. To enhance buy-in of scientists and engineers, programmatic access to the schema needs to be provided via open-source tools. The decomposition of such flexible structured data sets between open-source and proprietary (e.g., informatics companies) servers will undoubtedly be a matter of much discussion in the coming years as the materials R&D community deliberates on how to construct federated databases to best serve the needs of microstructure informatics and materials design and development.
Uncertainty quantification describes the assessment of the uncertainty in a simulation (or experiment). The basic idea is that any development and execution of a model generates error. For example, limiting the scope of the phenomena included in a model results in error. Use of experimentally determined parameters results in error. The limitations of even verified numerical methods introduce errors. While it is challenging to quantify the errors at each scale, quantifying how those errors propagate across scales is an even more daunting task. This error analysis effectively comprises uncertainty quantification. The science of uncertainty quantification is relatively new and is the focus of considerable efforts in many communities, including materials. Reference Panchal, Kalidindi and McDowell39–41
A major focus of microstructure informatics is the quantification of uncertainty, which is dominated by the errors in the digital representations of the microstructures or associated process–structure and structure–property relations (so-called epistemic or reducible uncertainty) and the statistical or random error associated with the variation in the actual microstructures (aleatoric or irreducible uncertainty). The latter error can be quantified, as can the errors associated with representation of microstructure. While there have been some applications of uncertainty quantification to informatics techniques, Reference Ganguly, Kong, Broderick and Rajan42 this is still a growing area of research. Yet another type of uncertainty is that of model form or structure, since description of materials phenomena can be approached with several types of models. Management of uncertainty, propagation of uncertainty in multiscale model chains, consideration of uncertainty in model assumptions and forms in addition to parameters, and assignment of performance margins are major considerations.
To this end, a recent report 27 addresses many of the greatest challenges and opportunities for multiscale modeling. It should be noted that several of the key recommendations relate to uncertainty, for example, to “address uncertainty quantification and propagation across multiple models describing a range of material length and time scales.” Other recommendations deal with the need for strong bidirectional coupling methods across scales for evolving microstructure, consideration of rare events and extreme value microstructure distributions, multiresolution (or multiscale) multiphysics free-energy functions, and addressing the role of phase nucleation and interfacial properties. All of these areas offer considerable challenges to microstructure informatics and should be addressed by ensuring these approaches are sufficiently well-grounded, linked to the underlying physics and chemistry to the greatest extent possible, sophisticated, and robust. This is one distinguishing feature of informatics applied to materials, especially materials with hierarchical microstructures.
Acknowledgments
D.L.M. is grateful for the support of the Institute for Materials at Georgia Tech, as well as the Carter N. Paden Jr. Distinguished Chair in Metals Processing. The work of R.A.L. was supported at the Ames Laboratory by the US Department of Energy, Office of Basic Energy Sciences, Division of Materials Sciences and Engineering under Contract No. DE-AC02–07CH11358.