No CrossRef data available.
Published online by Cambridge University Press: 15 February 2011
The NMR chemical shift anisotropy (CSA) has a temperature dependence as a result of thermal motions of the NMR site. For slow motions of a polymer chain at or near the glass transition, Tg, the CSA begins to decrease, with the characteristic powder pattern features, shoulders and divergence, approaching one another. This motional narrowing can be interpreted to yield the correlation time of the thermal motions. If Δ is the rigid-lattice shoulder to shoulder chemical shift anisotropy and τ is the correlation time of the slowmotion of the polymer chains, the total fractional shift, δ/Δ, for the general asymmetric case is found to be
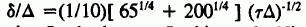
derived using Lee's theory. In this work, Nitrocellulose isotopically highly enriched with 15N was studied at four temperatures between 27° and 120° Celsius. To circumvent signal-to-noise problems in obtaining CSA data from a polycrystalline/amorphous sample, we used the Magic Angle Spinning (MAS) technique of Herzfeld and Berger. The principal values of the chemical shift tensor were then obtained from the relative intensities of the spinning sidebands in the MAS NMR spectrum. Correlation times were found to be of the order of 400 ms at 70°C, and 17 ms at 120°C.