No CrossRef data available.
Article contents
Simulation of Under- and Supersaturation of Gallium Vacancies in Gallium Arsenide During Silicon in- and Outdiffusion
Published online by Cambridge University Press: 10 February 2011
Abstract
The diffusivity of Si in GaAs shows a dependence on the cubic power of its concentration or the concentration of electrons n under both in- and outdiffusion conditions. Hence, the diffusion of Si in GaAs is consistent with the Fermi-level effect model invoking the triply-negatively-charged Ga vacancies, 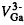 , as the point defect species responsible for diffusion to occur on the Ga sublattice under n-doping condition. However, the Si diffusivity values of the indiffusion cases is several orders of magnitude smaller than those of the outdiffusion cases at the same Si concentrations. This means that the two apparent Si diffusivity values under intrinsic conditions will contain also the same discrepancy, which has been previously assessed to be due to a
, as the point defect species responsible for diffusion to occur on the Ga sublattice under n-doping condition. However, the Si diffusivity values of the indiffusion cases is several orders of magnitude smaller than those of the outdiffusion cases at the same Si concentrations. This means that the two apparent Si diffusivity values under intrinsic conditions will contain also the same discrepancy, which has been previously assessed to be due to a 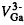 undersaturation in indiffusion cases and a
undersaturation in indiffusion cases and a 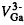 supersaturation in outdiffusion cases. In this study we have calculated the
supersaturation in outdiffusion cases. In this study we have calculated the 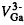 under- and supersaturation values using the known Si diffusivities. We found that the GaAs surface states play a key role in the development of the
under- and supersaturation values using the known Si diffusivities. We found that the GaAs surface states play a key role in the development of the 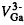 under- and supersaturations.
under- and supersaturations.
- Type
- Research Article
- Information
- Copyright
- Copyright © Materials Research Society 1998


