Hostname: page-component-6bb9c88b65-2jdt9 Total loading time: 0 Render date: 2025-07-17T23:55:17.883Z Has data issue: false hasContentIssue false
  • English
  • Français

6-vertex theorem for closed planar curve which bounds an immersed surface with non-zero genus

Published online by Cambridge University Press:  22 January 2016

Masaaki Umehara
Masaaki Umehara*
Affiliation:
Department of Mathematics, Faculty of Science, Osaka University, Toyonaka, Osaka 560, Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A vertex of a planar curve γ of class 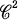is a point which attains a local maximum or minimum of its curvature function. By the definition, the number of vertices are even whenever it is finite. As a generalization of famous four vertex theorem, Pinkall [P] showed that a closed curve γ has at least 4 vertices if it bounds an immersed surface, and he conjectured that γ has at least 4g + 2 vertices when the surface has genus g.

Information

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 134 , June 1994 , pp. 75 - 89
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1994

References

[COT] Cairns, G., Õzdemir, M. and Tjaden, E. H., A counterexample to a conjecture of U. pinkall, Topology, 31 (1992), 557–558.Google Scholar
[J] Jackson, S. B., Vertices of plane curves, Bull. Amer. Math. Soc., 50 (1944), 564–578.Google Scholar
[KB] Kauffiman, L. H. and Banchoff, T. F., Immersions and Mod-2 quadratic forms, Amer. Math. Monthly, 84 (1977), 168–185.Google Scholar
[P] Pinkall, U., On the four-vertex theorem, Aequat, Math., 34 (1987), 221–230.Google Scholar
[W] Whitney, H., On regular closed curves in the plane, Comp. Math., 4 (1937), 276–284.Google Scholar