Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-02-12T07:17:10.355Z Has data issue: false hasContentIssue false
  • English
  • Français

CHARACTERIZING THE MOD-$\ell$ LOCAL LANGLANDS CORRESPONDENCE BY NILPOTENT GAMMA FACTORS

Part of: Algebraic number theory: local and $p$-adic fields Representation theory of groups

Published online by Cambridge University Press:  12 May 2020

GILBERT MOSS Open the ORCID record for GILBERT MOSS [Opens in a new window]
GILBERT MOSS*
Affiliation:
Department of Mathematics, University of Utah, Salt Lake City, UT84112, USA email moss@math.utah.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 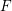$F$ be a 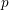$p$-adic field and choose 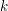$k$ an algebraic closure of 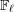$\mathbb{F}_{\ell }$, with $\ell$ different from $p$. We define “nilpotent lifts” of irreducible generic 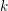$k$-representations of 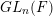$GL_{n}(F)$, which take coefficients in Artin local $k$-algebras. We show that an irreducible generic $\ell$-modular representation $\unicode[STIX]{x1D70B}$ of 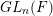$GL_{n}(F)$ is uniquely determined by its collection of Rankin–Selberg gamma factors 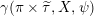$\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D70B}\times \widetilde{\unicode[STIX]{x1D70F}},X,\unicode[STIX]{x1D713})$ as 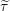$\widetilde{\unicode[STIX]{x1D70F}}$ varies over nilpotent lifts of irreducible generic 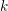$k$-representations $\unicode[STIX]{x1D70F}$ of 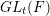$GL_{t}(F)$ for $t=1,\ldots ,\lfloor \frac{n}{2}\rfloor$. This gives a characterization of the mod-$\ell$ local Langlands correspondence in terms of gamma factors, assuming it can be extended to a surjective local Langlands correspondence on nilpotent lifts.

MSC classification

Primary: 11S37: Langlands-Weil conjectures, nonabelian class field theory 20C20: Modular representations and characters
Type
Article
Information
Nagoya Mathematical Journal , Volume 244 , December 2021 , pp. 119 - 135
Check for updates
Copyright
© 2020 Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, M., Liu, B., Stevens, S. and Kam-Fai Tam, G., On the sharpness of the bound for the local converse theorem of p-adic GL prime , Proc. Amer. Math. Soc. Ser. B 5 (2018), 6–17.CrossRefGoogle Scholar
Bushnell, C. and Henniart, G., The Local Langlands Conjecture for GL (2), Springer, Berlin, Heidelberg, 2006.CrossRefGoogle Scholar
Chai, J., Bessel functions and local converse conjecture of Jacquet , J. EMS 21 (2019), 1703–1728.Google Scholar
Deligne, P., “ Les constantes des equations fonctionelles des fonctions L ”, in Modular Functions of One Variable II, Lecture Notes In Mathematics, 349 , (eds. Deligne, P. and Kuijk, W.) Spring, Berlin, Heidelberg, 1973.CrossRefGoogle Scholar
Emerton, M. and Helm, D., The local Langlands correspondence for GL (n) in families , Ann. Sci. Éc. Norm. Supér. (4) 47 (2014), 655–722.Google Scholar
Helm, D., The Bernstein center of the category of smooth W (k)[GLn (F)]-modules , Forum Math. Sigma 4 (2016), e11, 98 pages.CrossRefGoogle Scholar
Helm, D., Whittaker models and the integral Bernstein center for GL (n) , Duke Math. J. 165(9) (2016), 1597–1628.CrossRefGoogle Scholar
Henniart, G., Caracterisation de la correspondance de langlands locale par les facteurs 𝜖 de paires , Invent. Math. 113 (1993), 339–350.CrossRefGoogle Scholar
Helm, D. and Moss, G., Deligne–Langlands gamma factors in families, preprint, 2015,arXiv:1510.08743.Google Scholar
Helm, D. and Moss, G., Converse theorems and the local Langlands correspondence in families , Invent. Math. 214 (2018), 999–1022.CrossRefGoogle ScholarPubMed
Harris, M. and Taylor, R., On the geometry and cohomology of some simple Shimura varieties , Ann. Math. Stud. (151) (2001).Google Scholar
Jacquet, H. and Langlands, R., Automorphic Forms on GL (2), Lecture notes in Mathematics, 114 , Springer, Berlin–Heidelberg, 1970.CrossRefGoogle Scholar
Jacquet, H. and Liu, B., On the local converse theorem for p-adic GL n , Amer. J. Math. 140(5) (2018), 1399–1422.CrossRefGoogle Scholar
Jacquet, H., Piatetski-Shapiro, I. I. and Shalika, J., Rankin–Selberg convolutions , Amer. J. Math. 105(2) (1983), 367–464.CrossRefGoogle Scholar
Kurinczuk, R. and Matringe, N., Rankin–Selberg local factors modulo ℓ , Selecta Math. 23 (2017), 767–811.CrossRefGoogle Scholar
Kurinczuk, R. and Matringe, N., The $\ell$ -modular local Langlands correspondence and local factors, doi:10.1017/S1474748019000586.CrossRefGoogle Scholar
Liu, B. and Moss, G., On the local converse theorem and descent theorem in families , Math. Z. (2019), doi:10.1007/s00209-019-02350-5.Google Scholar
Laumon, G., Rapoport, M. and Stuhler, U., D-elliptic sheaves and the Langlands correspondence , Invent. Math. 113 (1993), 217–338.CrossRefGoogle Scholar
Mínguez, A., Fonctions Zêta ℓ-modulaires , Nagoya Math. J. 208 (2012), 39–65.CrossRefGoogle Scholar
Moss, G., Gamma factors of pairs and a local converse theorem in families , Int. Math. Res. Not. IMRN 2016(16) (2016), 4903–4936.10.1093/imrn/rnv299CrossRefGoogle Scholar
Moss, G., Interpolating local constants in families , Math. Res. Lett. 23(6) (2016), 1789–1817.Google Scholar
Nien, C., A proof of the finite field analogue of Jacquet’s conjecture , Amer. J. Math. 136(3) (2014), 653–674.CrossRefGoogle Scholar
Paige, D., The projective envelope of a cuspidal representation of a finite linear group , J. Number Theory 136 (2014), 354–374.CrossRefGoogle Scholar
Vigneras, M.-F., Representations ℓ-modulaires d’un groupe reductif p-adique avec ℓ different de p , Birkhauser, Boston, 1996.Google Scholar
Vigneras, M.-F., Congruences modulo ℓ between 𝜖 factors for cuspidal representations of GL (2) , J. Théor. Nombres Bordeaux (2) (2000), 571–580.CrossRefGoogle Scholar
Vignéras, M.-F., Correspondance de Langlands semi-simple pour GL n(F) modulo ℓ≠p , Invent. Math. 144 (2001), 177–223.Google Scholar