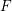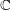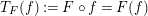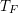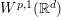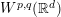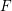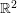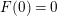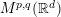Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kobayashi, Masaharu
and
Sato, Enji
2022.
Operating Functions on $$A^q_s({{\mathbf {T}}})$$.
Journal of Fourier Analysis and Applications,
Vol. 28,
Issue. 3,
Kobayashi, Masaharu
and
Sato, Enji
2022.
A note on operating functions of modulation spaces.
Journal of Pseudo-Differential Operators and Applications,
Vol. 13,
Issue. 4,
Ferreira, Lucas C. F.
and
Lagoin, Wender S.
2023.
An approach to elliptic equations with nonlinear gradient terms via a modulation framework.
Bulletin of Mathematical Sciences,
Vol. 13,
Issue. 03,
Biswas, Md Hasan Ali
and
Manna, Ramesh
2024.
Nonlinear operations and factorizations on a class of affine modulation spaces.
Forum Mathematicum,