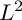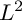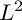Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Guan, Qi’an
Mi, Zhitong
and
Yuan, Zheng
2023.
Boundary Points, Minimal $$L^2$$ Integrals and Concavity Property "Equation missing" : Vector Bundles.
The Journal of Geometric Analysis,
Vol. 33,
Issue. 9,
Guan, Qi An
Mi, Zhi Tong
and
Yuan, Zheng
2024.
Boundary Points, Minimal L2 Integrals and Concavity Property III—Linearity on Riemann Surfaces and Fibrations over Open Riemann Surfaces.
Acta Mathematica Sinica, English Series,
Vol. 40,
Issue. 9,
p.
2091.
Guan, Qi'an
Mi, Zhitong
and
Yuan, Zheng
2024.
Concavity property of minimal L2 integrals with Lebesgue measurable gain II.
Advances in Mathematics,
Vol. 450,
Issue. ,
p.
109766.
Guan, Qi’an
Sun, Xun
and
Yuan, Zheng
2024.
A remark on a weighted version of Suita conjecture for higher derivatives.
Mathematische Zeitschrift,
Vol. 307,
Issue. 1,
Guan, Qi’an
Mi, Zhitong
and
Yuan, Zheng
2024.
Optimal $$L^2$$ Extension for Holomorphic Vector Bundles with Singular Hermitian Metrics.
Peking Mathematical Journal,
Guan, Qi’an
Mi, Zhitong
and
Yuan, Zheng
2024.
Boundary points, minimal L2 integrals and concavity property II: Weakly pseudoconvex Kähler manifolds.
Science China Mathematics,
Vol. 67,
Issue. 7,
p.
1665.
Bao, Shijie
Guan, Qi’an
and
Yuan, Zheng
2025.
Boundary points, minimal $$L^{2}$$ integrals and concavity property.
Mathematische Annalen,
Vol. 391,
Issue. 4,
p.
5809.
GUAN, Qi'an
MI, Zhitong
and
YUAN, Zheng
2025.
Guan–Zhou's unified version of optimal $L^{2}$ extension theorem on weakly pseudoconvex Kähler manifolds.
Journal of the Mathematical Society of Japan,
Vol. 77,
Issue. 1,
Bao, Shijie
Guan, Qi’an
and
Yuan, Zheng
2025.
Concavity property of minimal L2 integrals with Lebesgue measurable gain VI: Fibrations over products of open Riemann surfaces.
Science China Mathematics,