No CrossRef data available.
Article contents
THE HYPERELLIPTIC THETA MAP AND OSCULATING PROJECTIONS
Published online by Cambridge University Press: 04 December 2020
Abstract
Let C be a hyperelliptic curve of genus 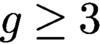 $g \geq 3$
. In this paper, we give a new geometric description of the theta map for moduli spaces of rank 2 semistable vector bundles on C with trivial determinant. In order to do this, we describe a fibration of (a birational model of) the moduli space, whose fibers are GIT quotients
$g \geq 3$
. In this paper, we give a new geometric description of the theta map for moduli spaces of rank 2 semistable vector bundles on C with trivial determinant. In order to do this, we describe a fibration of (a birational model of) the moduli space, whose fibers are GIT quotients 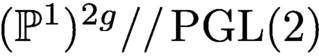 $(\mathbb {P}^1)^{2g}//\text {PGL(2)}$
. Then, we identify the restriction of the theta map to these GIT quotients with some explicit degree 2 osculating projection. As a corollary of this construction, we obtain a birational inclusion of a fibration in Kummer
$(\mathbb {P}^1)^{2g}//\text {PGL(2)}$
. Then, we identify the restriction of the theta map to these GIT quotients with some explicit degree 2 osculating projection. As a corollary of this construction, we obtain a birational inclusion of a fibration in Kummer 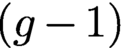 $(g-1)$
-varieties over
$(g-1)$
-varieties over 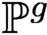 $\mathbb {P}^g$
inside the ramification locus of the theta map.
$\mathbb {P}^g$
inside the ramification locus of the theta map.
- Type
- Article
- Information
- Copyright
- © 2020 The Authors. The publishing rights in this article are licenced to Foundation Nagoya Mathematical Journal under an exclusive license
Footnotes
Michele Bolognesi is member of the research groups GAGC and GNSAGA, whose support is acknowledged.
References
 ${\mathbf{\mathcal{SU}}}_C(2)$
and the moduli of pointed rational curves
, J. Algebraic Geom. 24 (2015), no. 2, 283–310.CrossRefGoogle Scholar
${\mathbf{\mathcal{SU}}}_C(2)$
and the moduli of pointed rational curves
, J. Algebraic Geom. 24 (2015), no. 2, 283–310.CrossRefGoogle Scholar ${\mathbf{\mathcal{M}}}_{0,2n}^{GIT}$
, Bull. Lond. Math. Soc. 43 (2011), no. 3, 583–596.10.1112/blms/bdq125CrossRefGoogle Scholar
${\mathbf{\mathcal{M}}}_{0,2n}^{GIT}$
, Bull. Lond. Math. Soc. 43 (2011), no. 3, 583–596.10.1112/blms/bdq125CrossRefGoogle Scholar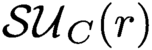 ${\mathbf{\mathcal{SU}}}_C(r)$
, Int. J. Math. 23 (2012), no. 4, 1250037.CrossRefGoogle Scholar
${\mathbf{\mathcal{SU}}}_C(r)$
, Int. J. Math. 23 (2012), no. 4, 1250037.CrossRefGoogle Scholar ${\mathbf{\mathcal{SU}}}_C{\left(2,2d\right)}^s$
is very ample if
${\mathbf{\mathcal{SU}}}_C{\left(2,2d\right)}^s$
is very ample if
 ${\overline{M}}_{0,n}$
, J. Algebraic Geom. 2 (1993), no. 2, 239–262.Google Scholar
${\overline{M}}_{0,n}$
, J. Algebraic Geom. 2 (1993), no. 2, 239–262.Google Scholar ${\overline{M}}_{0,n}$
. In
Handbook of Moduli. volume 25 of Adv. Lect. Math. (ALM)
II, Int. Press, Somerville, MA, 2013, 115–130.Google Scholar
${\overline{M}}_{0,n}$
. In
Handbook of Moduli. volume 25 of Adv. Lect. Math. (ALM)
II, Int. Press, Somerville, MA, 2013, 115–130.Google Scholar


