Article contents
KRONECKER LIMIT FUNCTIONS AND AN EXTENSION OF THE ROHRLICH–JENSEN FORMULA
Published online by Cambridge University Press: 11 April 2023
Abstract
In [20], Rohrlich proved a modular analog of Jensen’s formula. Under certain conditions, the Rohrlich–Jensen formula expresses an integral of the log-norm 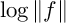 $\log \Vert f \Vert $ of a
$\log \Vert f \Vert $ of a 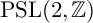 ${\mathrm {PSL}}(2,{\mathbb {Z}})$ modular form f in terms of the Dedekind Delta function evaluated at the divisor of f. In [2], the authors re-interpreted the Rohrlich–Jensen formula as evaluating a regularized inner product of
${\mathrm {PSL}}(2,{\mathbb {Z}})$ modular form f in terms of the Dedekind Delta function evaluated at the divisor of f. In [2], the authors re-interpreted the Rohrlich–Jensen formula as evaluating a regularized inner product of 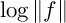 $\log \Vert f \Vert $ and extended the result to compute a regularized inner product of
$\log \Vert f \Vert $ and extended the result to compute a regularized inner product of 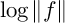 $\log \Vert f \Vert $ with what amounts to powers of the Hauptmodul of
$\log \Vert f \Vert $ with what amounts to powers of the Hauptmodul of 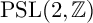 $\mathrm {PSL}(2,{\mathbb {Z}})$. In the present article, we revisit the Rohrlich–Jensen formula and prove that in the case of any Fuchsian group of the first kind with one cusp it can be viewed as a regularized inner product of special values of two Poincaré series, one of which is the Niebur–Poincaré series and the other is the resolvent kernel of the Laplacian. The regularized inner product can be seen as a type of Maass–Selberg relation. In this form, we develop a Rohrlich–Jensen formula associated with any Fuchsian group
$\mathrm {PSL}(2,{\mathbb {Z}})$. In the present article, we revisit the Rohrlich–Jensen formula and prove that in the case of any Fuchsian group of the first kind with one cusp it can be viewed as a regularized inner product of special values of two Poincaré series, one of which is the Niebur–Poincaré series and the other is the resolvent kernel of the Laplacian. The regularized inner product can be seen as a type of Maass–Selberg relation. In this form, we develop a Rohrlich–Jensen formula associated with any Fuchsian group 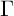 $\Gamma $ of the first kind with one cusp by employing a type of Kronecker limit formula associated with the resolvent kernel. We present two examples of our main result: First, when
$\Gamma $ of the first kind with one cusp by employing a type of Kronecker limit formula associated with the resolvent kernel. We present two examples of our main result: First, when 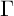 $\Gamma $ is the full modular group
$\Gamma $ is the full modular group 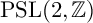 ${\mathrm {PSL}}(2,{\mathbb {Z}})$, thus reproving the theorems from [2]; and second when
${\mathrm {PSL}}(2,{\mathbb {Z}})$, thus reproving the theorems from [2]; and second when 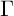 $\Gamma $ is an Atkin–Lehner group
$\Gamma $ is an Atkin–Lehner group 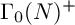 $\Gamma _{0}(N)^+$, where explicit computations of inner products are given for certain levels N when the quotient space
$\Gamma _{0}(N)^+$, where explicit computations of inner products are given for certain levels N when the quotient space 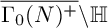 $\overline {\Gamma _{0}(N)^+}\backslash \mathbb {H}$ has genus zero, one, and two.
$\overline {\Gamma _{0}(N)^+}\backslash \mathbb {H}$ has genus zero, one, and two.
MSC classification
Information
- Type
- Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Foundation Nagoya Mathematical Journal
Footnotes
J.J. acknowledges grant support from several PSC-CUNY Awards, which are jointly funded by the Professional Staff Congress and The City University of New York.
References
- 1
- Cited by


