Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-10T20:14:49.070Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE ASSOCIATED PRIMES OF LOCAL COHOMOLOGY

Part of: General commutative ring theory Commutative algebra: Homological methods Chain conditions, finiteness conditions

Published online by Cambridge University Press:  05 February 2018

HAILONG DAO  and
PHAM HUNG QUY
HAILONG DAO
Affiliation:
Department of Mathematics, University of Kansas, Lawrence, KS 66045-7523, USA email hdao@ku.edu
PHAM HUNG QUY
Affiliation:
Department of Mathematics, FPT University Ha Noi, and Thang Long Institute of Mathematics and Applied Sciences, Thang Long University Ha Noi, Vietnam email quyph@fe.edu.vn
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 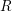$R$ be a commutative Noetherian ring of prime characteristic 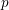$p$. In this paper, we give a short proof using filter regular sequences that the set of associated prime ideals of 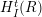$H_{I}^{t}(R)$ is finite for any ideal 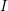$I$ and for any 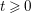$t\geqslant 0$ when 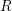$R$ has finite 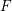$F$-representation type or finite singular locus. This extends a previous result by Takagi–Takahashi and gives affirmative answers for a problem of Huneke in many new classes of rings in positive characteristic. We also give a criterion about the singularities of 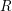$R$ (in any characteristic) to guarantee that the set 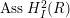$\operatorname{Ass}H_{I}^{2}(R)$ is always finite.

MSC classification

Primary: 13D45: Local cohomology 13A35: Characteristic $p$ methods (Frobenius endomorphism) and reduction to characteristic $p$; tight closure 13E99: None of the above, but in this section
Type
Article
Information
Nagoya Mathematical Journal , Volume 237 , March 2020 , pp. 1 - 9
Copyright
© 2018 Foundation Nagoya Mathematical Journal  

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This paper was done while the second author was visiting Vietnam Institute for Advanced Study in Mathematics.

References

Asadollahi, J. and Schenzel, P., Some results on associated primes of local cohomology modules , Jpn. J. Math. 29 (2003), 285–296.Google Scholar
Bahmanpour, K. and Quy, P. H., Localization at countably infinitely many prime ideals and applications , J. Algebra Appl. 15 (2016), 1650045 (6pages).Google Scholar
Bhatt, B., Blickle, M., Lyubeznik, G., Singh, A. and Zhang, W., Local cohomology modules of a smooth ℤ-algebra have finitely many associated primes , Invent. Math. 197 (2014), 509–519.Google Scholar
Brodmann, M. and Faghani, A. L., A finiteness result for associated primes of local cohomology modules , Proc. Amer. Math. Soc. 128 (2000), 2851–2853.Google Scholar
Brodmann, M. and Sharp, R. Y., Local Cohomology: An Algebraic Introduction with Geometric Applications, Cambridge University Press, Cambridge, 1998.Google Scholar
Hochster, M. and Núñez-Betancourt, L., Support of local cohomology modules over hypersurfaces and rings with FFRT , Math. Res. Lett. 24 (2017), 401–420.Google Scholar
Huneke, C., “ Problems on local cohomology ”, in Free Resolutions in Commutative Algebra and Algebraic Geometry (Sundance, UT, 1990), Res. Notes Math. 2 , Jones and Bartlett, Boston, MA, 1992, 93–108.Google Scholar
Huneke, C., Katz, D. and Marley, T., On the support of local cohomology , J. Algebra 322 (2009), 3194–3211.Google Scholar
Huneke, C. and Sharp, R. Y., Bass numbers of local cohomology modules , Trans. Amer. Math. Soc. 339 (1993), 765–779.Google Scholar
Katzman, M., An example of an infinite set of associated primes of a local cohomology module , J. Algebra 252 (2002), 161–166.Google Scholar
Kunz, E., Characterization of regular local rings for characteristic p , Amer. J. Math. 91 (1969), 772–784.Google Scholar
Lyubeznik, G., Finiteness properties of local cohomology modules (an application of D-modules to commutative algebra) , Invent. Math. 113 (1993), 41–55.Google Scholar
Lyubeznik, G., F-modules: applications to local cohomology and D-modules in characteristic p > 0 , J. Reine Angew. Math. 491 (1997), 65–130.+0+,+J.+Reine+Angew.+Math.+491+(1997),+65–130.>Google Scholar
Marley, T., The associated primes of local cohomology modules over rings of small dimension , Manuscripta Math. 104 (2001), 519–525.Google Scholar
Nagel, U. and Schenzel, P., “ Cohomological annihilators and Castelnuovo–Mumford regularity ”, in Commutative Algebra: Syzygies, Multiplicities, and Birational Algebra, Contemp. Math. 159 , Amer. Math. Soc., Providence, RI, 1994, 307–328.Google Scholar
Núñez-Betancourt, L., Local cohomology properties of direct summands , J. Pure Appl. Algebra 216 (2012), 2137–2140.Google Scholar
Patakfalvi, Z. and Schwede, K., Depth of F-singularities and base change of relative canonical sheaves , J. Inst. Math. Jussieu 13(1) (2014), 43–63.Google Scholar
Quy, P. H., A remark on the finiteness dimension , Comm. Algebra 41 (2014), 2048–2054.Google Scholar
Quy, P. H. and Shimomoto, K., F-injectivity and Frobenius closure of ideals in Noetherian rings of characteristic p > 0 , Adv. Math. 313 (2017), 127–166.+0+,+Adv.+Math.+313+(2017),+127–166.>Google Scholar
Singh, A. K., p-torsion elements in local cohomology modules , Math. Res. Lett. 7 (2000), 165–176.Google Scholar
Singh, A. K. and Swanson, I., Associated primes of local cohomology modules and of Frobenius powers , Int. Math. Res. Not. IMRN 33 (2004), 1703–1733.Google Scholar
Smith, K. E. and Van den Bergh, M., Simplicity of rings of differential operators in prime characteristic , Proc. Lond. Math. Soc. (3) 75 (1997), 32–62.Google Scholar
Takagi, S. and Takahashi, R., D-modules over rings with finite F-representation type , Math. Res. Lett. 15 (2008), 563–581.Google Scholar
Yao, Y., Modules with finite F-representation type , J. Lond. Math. Soc. (2) 72 (2005), 53–72.Google Scholar