Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-11T08:48:29.376Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE BILINEAR SQUARE FOURIER MULTIPLIER OPERATORS ASSOCIATED WITH 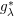$g_{\unicode[STIX]{x1D706}}^{\ast }$ FUNCTION

Part of: Harmonic analysis in several variables Integral, integro-differential, and pseudodifferential operators

Published online by Cambridge University Press:  28 August 2018

ZHENGYANG LI  and
QINGYING XUE Open the ORCID record for QINGYING XUE [Opens in a new window]
ZHENGYANG LI
Affiliation:
School of Mathematics and Computing Sciences, Hunan University of Science and Technology, Xiangtan 411201, People’s Republic of China email zhengyli@mail.bnu.edu.cn
QINGYING XUE*
Affiliation:
School of Mathematical Sciences, Beijing Normal University, Laboratory of Mathematics and Complex Systems, Ministry of Education, Beijing 100875, People’s Republic of China email qyxue@bnu.edu.cn
*
*Corresponding author.
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper will be devoted to study a class of bilinear square-function Fourier multiplier operator associated with a symbol $m$ defined by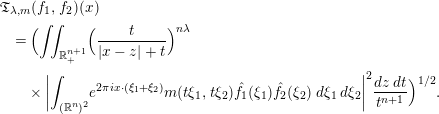

$$\begin{eqnarray}\displaystyle & & \displaystyle \mathfrak{T}_{\unicode[STIX]{x1D706},m}(f_{1},f_{2})(x)\nonumber\\ \displaystyle & & \displaystyle \quad =\Big(\iint _{\mathbb{R}_{+}^{n+1}}\Big(\frac{t}{|x-z|+t}\Big)^{n\unicode[STIX]{x1D706}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\bigg|\int _{(\mathbb{R}^{n})^{2}}e^{2\unicode[STIX]{x1D70B}ix\cdot (\unicode[STIX]{x1D709}_{1}+\unicode[STIX]{x1D709}_{2})}m(t\unicode[STIX]{x1D709}_{1},t\unicode[STIX]{x1D709}_{2})\hat{f}_{1}(\unicode[STIX]{x1D709}_{1})\hat{f}_{2}(\unicode[STIX]{x1D709}_{2})\,d\unicode[STIX]{x1D709}_{1}\,d\unicode[STIX]{x1D709}_{2}\bigg|^{2}\frac{dz\,dt}{t^{n+1}}\Big)^{1/2}.\nonumber\end{eqnarray}$$
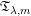A basic fact about $\mathfrak{T}_{\unicode[STIX]{x1D706},m}$ is that it is closely associated with the multilinear Littlewood–Paley 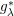$g_{\unicode[STIX]{x1D706}}^{\ast }$ function. In this paper we first investigate the boundedness of 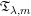$\mathfrak{T}_{\unicode[STIX]{x1D706},m}$ on products of weighted Lebesgue spaces. Then, the weighted endpoint 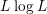$L\log L$ type estimate and strong estimate for the commutators of $\mathfrak{T}_{\unicode[STIX]{x1D706},m}$ will be demonstrated.

MSC classification

Primary: 42B25: Maximal functions, Littlewood-Paley theory 47G10: Integral operators
Type
Article
Information
Nagoya Mathematical Journal , Volume 239 , September 2020 , pp. 123 - 152
Check for updates
Copyright
© 2018 Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The second author was supported partly by NSFC (Nos. 11471041, 11671039, 11871101) and NSFC-DFG (No. 11761131002).

References

Bui, T. A. and Duong, X. T., On commutators of vector BMO functions and multilinear singular integrals with non-smooth kernels, J. Math. Anal. Appl. 371 (2010), 80–84.Google Scholar
Bui, T. A. and Duong, X. T., Weighted norm inequalities for multilinear operators and applications to multilinear Fourier multipliers, Bull. Sci. Math. 137(1) (2013), 63–75.10.1016/j.bulsci.2012.04.001Google Scholar
Chen, X., Xue, Q. and Yabuta, K., On multilinear Littlewood-Paley operators, Nonlinear Anal. 115 (2015), 25–40.Google Scholar
Coifman, R. R., Deng, D. and Meyer, Y., Domains de la racine carre de certains oprateurs differentiels accrtifs, Ann. Inst. Fourier (Grenoble) 33 (1983), 123–134.10.5802/aif.919Google Scholar
Coifman, R. R., McIntosh, A. and Meyer, Y., Lintegrale de Cauchy definit un operateur borne sur L 2 pour les courbes lips-chitziennes, Ann. of Math. (2) 116 (1982), 361–387.Google Scholar
Coifman, R. R. and Meyer, Y., On commutators of singular integrals and bilinear singular integrals, Trans. Amer. Math. Soc. 212 (1975), 315–331.10.1090/S0002-9947-1975-0380244-8Google Scholar
Coifman, R. R. and Meyer, Y., Commutateurs d’intégrales singulières et opérateurs multilinéaires, Ann. Inst. Fourier (Grenoble) 28 (1978), 177–202.Google Scholar
Coifman, R. R. and Meyer, Y., Au-delà des opérateurs pseudo-différentiels, Astérisque 57, Société Mathématique De France, Paris, 1978.Google Scholar
David, G. and Journé, J. L., Une caractrisation des oprateurs intgraux singuliers borns sur L 2(ℝn), C. R. Math. Acad. Sci. Paris 296 (1983), 761–764.Google Scholar
Fabes, E. B., Jerison, D. and Kenig, C., Multilinear Littlewood-Paley estimates with applications to partial differential equations, Proc. Natl Acad. Sci. 79 (1982), 5746–5750.10.1073/pnas.79.18.5746Google Scholar
Fabes, E. B., Jerison, D. and Kenig, C., Necessary and sufficient conditions for absolute continuity of elliptic harmonic measure, Ann. of Math. (2) 119 (1984), 121–141.10.2307/2006966Google Scholar
Fabes, E. B., Jerison, D. and Kenig, C., Multilinear square functions and partial differential equations, Amer. J. Math. 107 (1985), 1325–1368.Google Scholar
Fefferman, C., Inequalities for strongly singular convolution operators, Acta Math. 124 (1970), 9–36.10.1007/BF02394567Google Scholar
Fujita, M. and Tomita, N., Weighted norm inequalities for multilinear Fourier multipliers, Trans. Amer. Math. Soc. 364 (2012), 6335–6353.10.1090/S0002-9947-2012-05700-XGoogle Scholar
Grafakos, L. and Si, Z., The Hörmander multiplier theorem for multilinear operators, J. Reine Angew. Math. 668 (2012), 133–147.Google Scholar
Grafakos, L., Miyachi, A. and Tomita, N., On multilinear Fourier multipliers of limited smoothness, Canad. J. Math. 65(2) (2013), 299–330.Google Scholar
Grafakos, L. and Torres, R., Multilinear Calderón–Zygmund theory, Adv. Math. 165 (2002), 124–164.Google Scholar
Grafakos, L. and Torres, R. H., Maximal operator and weighted norm inequalities for multilinear singular integrals, Indiana Univ. Math. J. 51(5) (2002), 1261–1276.10.1512/iumj.2002.51.2114Google Scholar
Lerner, A. K., Ombrosi, S., Pérez, C., Torres, R. H. and Trujillo-González, R., New maximal functions and multiple weights for the multilinear Calderón–Zygmund theory, Adv. Math. 220(4) (2009), 1222–1264.10.1016/j.aim.2008.10.014Google Scholar
Li, K. and Sun, W., Weighted estimates for multilinear Fourier multipliers, Forum Math. 27(2) (2015), 1101–1116.Google Scholar
Li, W., Xue, Q. and Yabuta, K., Weighted version of Carleson measure and multilinear Fourier multiplier, Forum Math. 27(2) (2015), 787–805.Google Scholar
Muckenhoupt, B. and Wheeden, R. L., Norm inequalities for the Littlewood-Paley function g 𝜆∗, Trans. Amer. Math. Soc. 191 (1974), 95–111.Google Scholar
Shi, S., Xue, Q. and Yabuta, K., On the boundedness of multilinear Littlewood-Paley g 𝜆∗ function, J. Math. Pures Appl. 101(3) (2014), 394–413.Google Scholar
Stein, E. M., On some function of Littlewood-Paley and Zygmund, Bull. Amer. Math. Soc. 67 (1961), 99–101.10.1090/S0002-9904-1961-10515-6Google Scholar
Tomita, N., A Hörmander type multiplier theorem for multilinear operators, J. Funct. Anal. 259 (2010), 2028–2044.Google Scholar
Xue, Q., Peng, X. and Yabuta, K., On the theory of multilinear Littlewood-Paley g function, J. Math. Soc. Japan 67(2) (2015), 535–559.10.2969/jmsj/06720535Google Scholar
Xue, Q. and Yan, J., On multilinear square function and its applications to multilinear Littlewood-Paley operators with non-convolution type kernels, J. Math. Anal. Appl. 422 (2015), 1342–1362.Google Scholar
Zengyan, S., Xue, Q. and Yabuta, K., On the bilinear square Fourier multiplier operators and related multilinear square functions, Sci. China Math. 60(8) (2017), 1477–1502.Google Scholar