Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T07:16:05.550Z Has data issue: false hasContentIssue false
  • English
  • Français

Affine hypersurfaces with parallel cubic form

Published online by Cambridge University Press:  22 January 2016

Franki Dillen ,
Luc Vrancken  and
Sahnur Yaprak
Franki Dillen
Affiliation:
Katholieke Universiteit Leuven, Departement Wiskunde, Celestijnenlaan 200 B, B-3001 Leuven, Belgium
Luc Vrancken
Affiliation:
Katholieke Universiteit Leuven, Departement Wiskunde, Celestijnenlaan 200 B, B-3001 Leuven, Belgium
Sahnur Yaprak
Affiliation:
Katholieke Universiteit Leuven, Departement Wiskunde, Celestijnenlaan 200 B, B-3001 Leuven, Belgium The University of Ankara, The Faculty of Sciences, Tandoḡan, 06100, Ankara, Turkey
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

As is well known, there exists a canonical transversal vector field on a non-degenerate affine hypersurface M. This vector field is called the affine normal. The second fundamental form associated to this affine normal is called the affine metric. If M is locally strongly convex, then this affine metric is a Riemannian metric. And also, using the affine normal and the Gauss formula one can introduce an affine connection ∇ on M which is called the induced affine connection. 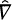Thus there are in general two different connections on M: one is the induced connection ∇ and the other is the Levi Civita connection of the affine metric h. The difference tensor K is defined by K(X, Y) = KXY — ∇XY — 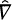XY. The cubic form C is defined by C = ∇h and is related to the difference tensor by

.

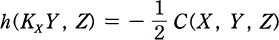Type
Research Article
Information
Nagoya Mathematical Journal , Volume 135 , September 1994 , pp. 153 - 164
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1994

References

[D] Dillen, F., Equivalence theorems in affine differential geometry, Geom. Dedicata, 32 (1989), 81–92.CrossRefGoogle Scholar
[DVl] Dillen, F., Vrancken, L., 3-dimensional affine hypersurfaces in R with parallel cubic form, Nagoya Math, J., 124 (1991), 41–53.Google Scholar
[DV2] Dillen, F., Calabi-type composition of affine spheres, Diff. Geom. and Appl, (to appear).Google Scholar
[DV3] Dillen, F., The classification of 3-dimensional homogeneous locally strongly convex affine hypersurfaces, Manuscripta Math., 80 (1993), 165–180.Google Scholar
[MN] Magid, M. and Nomizu, K., On affine surfaces whose cubic forms are parallel relative to the affine metric, Proc. Japan. Acad. Ser. A, 65 (1989), 215–218.Google Scholar
[N] Nomizu, K., Introduction to affine differential geometry, Part I, MPI/88–38, Bonn, 1988, Revised: Department of Mathematics, Brown University, 1989.Google Scholar
[NS] Nomizu, K., Sasaki, T., A new model of unimodular-affinely homogeneous surfaces, Manuscripta Math., 73 (1991), 39–44.CrossRefGoogle Scholar
[O’N] O’Neill, B., Semi-Riemannian geometry with applications to relativity, Academic Press, New York, 1983.Google Scholar
[VLS] Vrancken, L., Li, A.-M., Simon, U., Affine spheres with constant sectional curvature, Math. Z., 206 (1991), 651–658.CrossRefGoogle Scholar