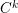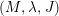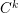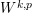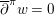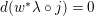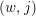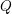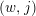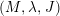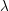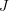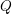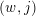1 Introduction
Let
![]() $(M,\unicode[STIX]{x1D709})$
be a contact manifold. Each contact form
$(M,\unicode[STIX]{x1D709})$
be a contact manifold. Each contact form
![]() $\unicode[STIX]{x1D706}$
of
$\unicode[STIX]{x1D706}$
of
![]() $\unicode[STIX]{x1D709}$
, that is, a one-form with
$\unicode[STIX]{x1D709}$
, that is, a one-form with
![]() $\ker \unicode[STIX]{x1D706}=\unicode[STIX]{x1D709}$
, canonically induces a splitting
$\ker \unicode[STIX]{x1D706}=\unicode[STIX]{x1D709}$
, canonically induces a splitting
Here
![]() $X_{\unicode[STIX]{x1D706}}$
is the Reeb vector field of
$X_{\unicode[STIX]{x1D706}}$
is the Reeb vector field of
![]() $\unicode[STIX]{x1D706}$
, which is uniquely determined by the equations
$\unicode[STIX]{x1D706}$
, which is uniquely determined by the equations
We denote by
![]() $\unicode[STIX]{x1D6F1}=\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D706}}:TM\rightarrow TM$
the idempotent, that is, an endomorphism satisfying
$\unicode[STIX]{x1D6F1}=\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D706}}:TM\rightarrow TM$
the idempotent, that is, an endomorphism satisfying
![]() $\unicode[STIX]{x1D6F1}^{2}=\unicode[STIX]{x1D6F1}$
such that
$\unicode[STIX]{x1D6F1}^{2}=\unicode[STIX]{x1D6F1}$
such that
![]() $\ker \unicode[STIX]{x1D6F1}=\mathbb{R}\{X_{\unicode[STIX]{x1D706}}\}$
and
$\ker \unicode[STIX]{x1D6F1}=\mathbb{R}\{X_{\unicode[STIX]{x1D706}}\}$
and
![]() $\text{Im}\,\unicode[STIX]{x1D6F1}=\unicode[STIX]{x1D709}$
. Denote by
$\text{Im}\,\unicode[STIX]{x1D6F1}=\unicode[STIX]{x1D709}$
. Denote by
![]() $\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}:TM\rightarrow \unicode[STIX]{x1D709}$
the associated projection.
$\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}:TM\rightarrow \unicode[STIX]{x1D709}$
the associated projection.
Definition 1.1. (Contact triad)
We call the triple
![]() $(M,\unicode[STIX]{x1D706},J)$
a contact triad of
$(M,\unicode[STIX]{x1D706},J)$
a contact triad of
![]() $(M,\unicode[STIX]{x1D709})$
if
$(M,\unicode[STIX]{x1D709})$
if
![]() $\unicode[STIX]{x1D706}$
is a contact form of
$\unicode[STIX]{x1D706}$
is a contact form of
![]() $(M,\unicode[STIX]{x1D709})$
, and
$(M,\unicode[STIX]{x1D709})$
, and
![]() $J$
is an endomorphism of
$J$
is an endomorphism of
![]() $TM$
with
$TM$
with
![]() $J^{2}=-\unicode[STIX]{x1D6F1}$
which we call
$J^{2}=-\unicode[STIX]{x1D6F1}$
which we call
![]() $CR$
-almost complex structure, such that the triple
$CR$
-almost complex structure, such that the triple
![]() $(\unicode[STIX]{x1D709},d\unicode[STIX]{x1D706}|_{\unicode[STIX]{x1D709}},J|_{\unicode[STIX]{x1D709}})$
defines a Hermitian vector bundle over
$(\unicode[STIX]{x1D709},d\unicode[STIX]{x1D706}|_{\unicode[STIX]{x1D709}},J|_{\unicode[STIX]{x1D709}})$
defines a Hermitian vector bundle over
![]() $M$
.
$M$
.
As long as no confusion arises, we abuse our notation
![]() $J$
also for its restriction to
$J$
also for its restriction to
![]() $\unicode[STIX]{x1D709}$
.
$\unicode[STIX]{x1D709}$
.
In [Reference Oh and WangOW2], the authors of the present paper called the pair
![]() $(w,j)$
a contact instanton, if
$(w,j)$
a contact instanton, if
![]() $(\unicode[STIX]{x1D6F4},j)$
is a (punctured) Riemann surface and
$(\unicode[STIX]{x1D6F4},j)$
is a (punctured) Riemann surface and
![]() $w:\unicode[STIX]{x1D6F4}\rightarrow M$
satisfies the following equations
$w:\unicode[STIX]{x1D6F4}\rightarrow M$
satisfies the following equations
A priori coercive
![]() $W^{k,2}$
-estimates for
$W^{k,2}$
-estimates for
![]() $w$
with
$w$
with
![]() $W^{1,2}$
-bound was established without involving symplectization. Moreover, the study of
$W^{1,2}$
-bound was established without involving symplectization. Moreover, the study of
![]() $W^{1,2}$
(or the derivative) bound and the definition of relevant energy is carried out by the Yong-Geun Oh in [Reference OhOh2].
$W^{1,2}$
(or the derivative) bound and the definition of relevant energy is carried out by the Yong-Geun Oh in [Reference OhOh2].
Furthermore, for the punctured domains
![]() $\dot{\unicode[STIX]{x1D6F4}}$
equipped with cylindrical metric near the puncture, the present authors proved the result of asymptotic subsequence uniform convergence to a Reeb orbit (which must be closed when the corresponding charge is vanishing) under the assumption that the
$\dot{\unicode[STIX]{x1D6F4}}$
equipped with cylindrical metric near the puncture, the present authors proved the result of asymptotic subsequence uniform convergence to a Reeb orbit (which must be closed when the corresponding charge is vanishing) under the assumption that the
![]() $\unicode[STIX]{x1D70B}$
-harmonic energy is finite and the
$\unicode[STIX]{x1D70B}$
-harmonic energy is finite and the
![]() $C^{0}$
-norm of derivative
$C^{0}$
-norm of derivative
![]() $dw$
is bounded. (Refer [Reference Oh and WangOW2, Section 6] for precise statement and Section 9 in the current paper for its review.) Based on this subsequence uniform convergence result, the present authors previously proved
$dw$
is bounded. (Refer [Reference Oh and WangOW2, Section 6] for precise statement and Section 9 in the current paper for its review.) Based on this subsequence uniform convergence result, the present authors previously proved
![]() $C^{\infty }$
exponential decay in [Reference Oh and WangOW2] when the contact form is nondegenerate. The proof is based on the so-called three-interval argument which is essentially different from the proofs for exponential convergence in existing literatures, for example, from those in [Reference Hofer, Wysocki and ZehnderHWZ1, Reference Hofer, Wysocki and ZehnderHWZ2, Reference Hofer, Wysocki and ZehnderHWZ4] which use the method of differential inequality.
$C^{\infty }$
exponential decay in [Reference Oh and WangOW2] when the contact form is nondegenerate. The proof is based on the so-called three-interval argument which is essentially different from the proofs for exponential convergence in existing literatures, for example, from those in [Reference Hofer, Wysocki and ZehnderHWZ1, Reference Hofer, Wysocki and ZehnderHWZ2, Reference Hofer, Wysocki and ZehnderHWZ4] which use the method of differential inequality.
The present paper is a sequel to the paper [Reference Oh and WangOW2] and the main purpose thereof is to generalize the exponential convergence result to the Morse–Bott case. In Part 2 of the current paper, we systematically develop the above mentioned three-interval method as a general framework and establish the result for Morse–Bott contact forms. (Corresponding results for pseudoholomorphic curves in symplectizations were provided by various authors including [Reference Hofer, Wysocki and ZehnderHWZ3, Reference BourgeoisBou, Reference BaoBa] and we suggest readers to compare our method with theirs.)
In general, the exponential convergence result is an important ingredient in the setup of the Fredholm theory and in the relevant gluing construction. In contact geometry, the moduli spaces of pseudoholomorphic curves with noncompact sources are used in defining the contact homology or setting up the framework of the symplectic field theory (SFT) (see e.g., [Reference Eliashberg, Givental and HoferEGH] for an introduction). In this regard, the Morse–Bott case provides important computable examples in contact geometry and in SFT. (See [Reference BourgeoisBou] for some examples of such computations based on the Morse–Bott framework of contact homology.) However, there are various subtleties in describing the structure of the Morse–Bott moduli spaces and the corresponding contact homology for the contact forms of Morse–Bott type, which have not been rigorously set up yet. One of the purposes of the current paper is to provide a careful geometric description of the locus of closed Reeb orbits and the corresponding tensorial proof of exponential decay results. Moreover, the abstract framework of the three-interval method we develop in this paper for the exponential decay proof can be easily applied to other evolution type of equations, and provides a general “black box” for the exponential decay.
The proof of the exponential decay result consists of two parts, one geometric and the other analytic. Part 1 is devoted to unveil the geometric structure, the precontact structure, carried by the loci
![]() $Q$
of the closed Reeb orbits of a Morse–Bott contact form
$Q$
of the closed Reeb orbits of a Morse–Bott contact form
![]() $\unicode[STIX]{x1D706}$
(see Section 1.1 for precise definition). We prove a canonical neighborhood theorem of any precontact manifold which is the contact analogue to Gotay’s on presymplectic manifolds [Reference GotayG], which we call the contact thickening of a precontact manifold. By using this neighborhood theorem, we obtain a canonical splitting of the tangent bundle
$\unicode[STIX]{x1D706}$
(see Section 1.1 for precise definition). We prove a canonical neighborhood theorem of any precontact manifold which is the contact analogue to Gotay’s on presymplectic manifolds [Reference GotayG], which we call the contact thickening of a precontact manifold. By using this neighborhood theorem, we obtain a canonical splitting of the tangent bundle
![]() $TM$
in terms of the precontact structure of
$TM$
in terms of the precontact structure of
![]() $Q$
and its thickening. Then we introduce the class consisting of
$Q$
and its thickening. Then we introduce the class consisting of
![]() $J$
’s adapted to
$J$
’s adapted to
![]() $Q$
(refer Section 8 for definition) besides the standard compatibility requirement to
$Q$
(refer Section 8 for definition) besides the standard compatibility requirement to
![]() $d\unicode[STIX]{x1D706}$
. At last we split the derivative
$d\unicode[STIX]{x1D706}$
. At last we split the derivative
![]() $dw$
of contact instanton
$dw$
of contact instanton
![]() $w$
into various components and study them separately. In this way, we are given the geometric framework which gets us ready to conduct the three-interval method provided in Part 2. Part 2 is then devoted to applying the enhanced version of the three-interval framework in proving the exponential convergence for the Morse–Bott case, which generalizes the one presented for the nondegenerate case in [Reference Oh and WangOW2].
$w$
into various components and study them separately. In this way, we are given the geometric framework which gets us ready to conduct the three-interval method provided in Part 2. Part 2 is then devoted to applying the enhanced version of the three-interval framework in proving the exponential convergence for the Morse–Bott case, which generalizes the one presented for the nondegenerate case in [Reference Oh and WangOW2].
Now we outline the main results in the present paper in more details.
1.1 Structure of the locus of closed Reeb orbits
Assume
![]() $\unicode[STIX]{x1D706}$
is a fixed contact form of the contact manifold
$\unicode[STIX]{x1D706}$
is a fixed contact form of the contact manifold
![]() $(M,\unicode[STIX]{x1D709})$
. For a closed Reeb orbit
$(M,\unicode[STIX]{x1D709})$
. For a closed Reeb orbit
![]() $\unicode[STIX]{x1D6FE}$
of period
$\unicode[STIX]{x1D6FE}$
of period
![]() $T>0$
, one can write
$T>0$
, one can write
![]() $\unicode[STIX]{x1D6FE}(t)=\unicode[STIX]{x1D719}^{t}(\unicode[STIX]{x1D6FE}(0))$
, where
$\unicode[STIX]{x1D6FE}(t)=\unicode[STIX]{x1D719}^{t}(\unicode[STIX]{x1D6FE}(0))$
, where
![]() $\unicode[STIX]{x1D719}^{t}=\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D706}}}^{t}$
is the flow of the Reeb vector field
$\unicode[STIX]{x1D719}^{t}=\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D706}}}^{t}$
is the flow of the Reeb vector field
![]() $X_{\unicode[STIX]{x1D706}}$
.
$X_{\unicode[STIX]{x1D706}}$
.
Denote by
![]() $\operatorname{Cont}(M,\unicode[STIX]{x1D709})$
the set of all contact one-forms with respect to the contact structure
$\operatorname{Cont}(M,\unicode[STIX]{x1D709})$
the set of all contact one-forms with respect to the contact structure
![]() $\unicode[STIX]{x1D709}$
, and by
$\unicode[STIX]{x1D709}$
, and by
![]() ${\mathcal{L}}(M)=C^{\infty }(S^{1},M)$
the space of loops
${\mathcal{L}}(M)=C^{\infty }(S^{1},M)$
the space of loops
![]() $z:S^{1}=\mathbb{R}/\mathbb{Z}\rightarrow M$
. Consider the bundle
$z:S^{1}=\mathbb{R}/\mathbb{Z}\rightarrow M$
. Consider the bundle
![]() ${\mathcal{L}}$
over the product
${\mathcal{L}}$
over the product
![]() $(0,\infty )\times {\mathcal{L}}(M)\times \operatorname{Cont}(M,\unicode[STIX]{x1D709})$
whose fiber at
$(0,\infty )\times {\mathcal{L}}(M)\times \operatorname{Cont}(M,\unicode[STIX]{x1D709})$
whose fiber at
![]() $(T,z,\unicode[STIX]{x1D706})$
is
$(T,z,\unicode[STIX]{x1D706})$
is
![]() $C^{\infty }(z^{\ast }TM)$
. The assignment
$C^{\infty }(z^{\ast }TM)$
. The assignment
defines a section of the bundle, where
![]() $(T,z)$
is a pair with a loop
$(T,z)$
is a pair with a loop
![]() $z$
parameterized over the unit interval
$z$
parameterized over the unit interval
![]() $S^{1}=[0,1]/\!\sim$
defined by
$S^{1}=[0,1]/\!\sim$
defined by
![]() $z(t)=\unicode[STIX]{x1D6FE}(Tt)$
for a Reeb orbit
$z(t)=\unicode[STIX]{x1D6FE}(Tt)$
for a Reeb orbit
![]() $\unicode[STIX]{x1D6FE}$
of period
$\unicode[STIX]{x1D6FE}$
of period
![]() $T$
. Notice that
$T$
. Notice that
![]() $(T,z,\unicode[STIX]{x1D706})\in \unicode[STIX]{x1D6F6}^{-1}(0):=\mathfrak{Reeb}(M,\unicode[STIX]{x1D709})$
if and only if there exists some Reeb orbit
$(T,z,\unicode[STIX]{x1D706})\in \unicode[STIX]{x1D6F6}^{-1}(0):=\mathfrak{Reeb}(M,\unicode[STIX]{x1D709})$
if and only if there exists some Reeb orbit
![]() $\unicode[STIX]{x1D6FE}:\mathbb{R}\rightarrow M$
with period
$\unicode[STIX]{x1D6FE}:\mathbb{R}\rightarrow M$
with period
![]() $T$
, such that
$T$
, such that
![]() $z(\cdot )=\unicode[STIX]{x1D6FE}(T\cdot )$
. Denote by
$z(\cdot )=\unicode[STIX]{x1D6FE}(T\cdot )$
. Denote by
for each
![]() $\unicode[STIX]{x1D706}\in \operatorname{Cont}(M,\unicode[STIX]{x1D709})$
. From the formula of a
$\unicode[STIX]{x1D706}\in \operatorname{Cont}(M,\unicode[STIX]{x1D709})$
. From the formula of a
![]() $T$
-periodic orbit
$T$
-periodic orbit
![]() $(T,\unicode[STIX]{x1D6FE})$
,
$(T,\unicode[STIX]{x1D6FE})$
,
![]() $T=\int _{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D706}$
. It follows that the period varies smoothly over
$T=\int _{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D706}$
. It follows that the period varies smoothly over
![]() $\unicode[STIX]{x1D6FE}$
.
$\unicode[STIX]{x1D6FE}$
.
The general Morse–Bott condition (Bott’s notion [Reference BottBot] of clean critical submanifold in general) for
![]() $\unicode[STIX]{x1D706}$
corresponds to the statement that every connected component of
$\unicode[STIX]{x1D706}$
corresponds to the statement that every connected component of
![]() $\mathfrak{Reeb}(M,\unicode[STIX]{x1D706})$
is a smooth submanifold of
$\mathfrak{Reeb}(M,\unicode[STIX]{x1D706})$
is a smooth submanifold of
![]() $(0,\infty )\times {\mathcal{L}}(M)$
and its tangent space at every pair
$(0,\infty )\times {\mathcal{L}}(M)$
and its tangent space at every pair
![]() $(T,z)\in \mathfrak{Reeb}(M,\unicode[STIX]{x1D706})$
therein coincides with
$(T,z)\in \mathfrak{Reeb}(M,\unicode[STIX]{x1D706})$
therein coincides with
![]() $\ker d_{(T,z)}\unicode[STIX]{x1D6F6}$
. Denote by
$\ker d_{(T,z)}\unicode[STIX]{x1D6F6}$
. Denote by
![]() $Q$
the locus of closed Reeb orbits contained in a fixed connected component of
$Q$
the locus of closed Reeb orbits contained in a fixed connected component of
![]() $\mathfrak{Reeb}(M,\unicode[STIX]{x1D706})$
. Throughout this paper, we also call
$\mathfrak{Reeb}(M,\unicode[STIX]{x1D706})$
. Throughout this paper, we also call
![]() $Q$
a Morse–Bott submanifold when we want to emphasize its manifold structure.
$Q$
a Morse–Bott submanifold when we want to emphasize its manifold structure.
However, when one tries to set up the moduli space of contact instantons for Morse–Bott contact forms, more requirements are needed and we recall the definition that Bourgeois adopted in [Reference BourgeoisBou]. (Strictly speaking, we also need to take suitable completions of
![]() ${\mathcal{L}}(M)$
and
${\mathcal{L}}(M)$
and
![]() $\operatorname{Cont}(M,\unicode[STIX]{x1D709})$
but we ignore this point which does not play any role in our main discussion.)
$\operatorname{Cont}(M,\unicode[STIX]{x1D709})$
but we ignore this point which does not play any role in our main discussion.)
Definition 1.2. (Equivalent to Definition 1.7 [Reference BourgeoisBou])
A contact form
![]() $\unicode[STIX]{x1D706}$
is called be of Morse–Bott type, if it satisfies the following:
$\unicode[STIX]{x1D706}$
is called be of Morse–Bott type, if it satisfies the following:
(1) every connected component of
 $\mathfrak{Reeb}(M,\unicode[STIX]{x1D706})$
is a smooth submanifold of
$\mathfrak{Reeb}(M,\unicode[STIX]{x1D706})$
is a smooth submanifold of
 $(0,\infty )\times {\mathcal{L}}(M)$
with its tangent space at every pair
$(0,\infty )\times {\mathcal{L}}(M)$
with its tangent space at every pair
 $(T,z)\in \mathfrak{Reeb}(M,\unicode[STIX]{x1D706})$
therein coincides with
$(T,z)\in \mathfrak{Reeb}(M,\unicode[STIX]{x1D706})$
therein coincides with
 $\ker d_{(T,z)}\unicode[STIX]{x1D6F6}$
;
$\ker d_{(T,z)}\unicode[STIX]{x1D6F6}$
;(2) the locus
 $Q$
is embedded;
$Q$
is embedded;(3) the 2-form
 $d\unicode[STIX]{x1D706}|_{Q}$
associated to the locus
$d\unicode[STIX]{x1D706}|_{Q}$
associated to the locus
 $Q$
of closed Reeb orbits has constant rank.
$Q$
of closed Reeb orbits has constant rank.
Here Condition (1) corresponds to Bott’s notion of Morse–Bott critical manifolds which we name as standard Morse–Bott type. While
![]() $\mathfrak{Reeb}(M,\unicode[STIX]{x1D706})$
is a smooth submanifold, the orbit locus
$\mathfrak{Reeb}(M,\unicode[STIX]{x1D706})$
is a smooth submanifold, the orbit locus
![]() $Q\subset M$
of
$Q\subset M$
of
![]() $\mathfrak{Reeb}(M,\unicode[STIX]{x1D706})$
is in general only an immersed submanifold and could have multiple sheets along the locus of multiple orbits. Therefore, we impose Condition (2). In general, the restriction of the two-form
$\mathfrak{Reeb}(M,\unicode[STIX]{x1D706})$
is in general only an immersed submanifold and could have multiple sheets along the locus of multiple orbits. Therefore, we impose Condition (2). In general, the restriction of the two-form
![]() $d\unicode[STIX]{x1D706}$
to
$d\unicode[STIX]{x1D706}$
to
![]() $Q$
has varying rank. It is still not clear whether the exponential estimates we derive in this paper holds in this general context because our proof strongly relies on the existence of canonical model of neighborhoods of
$Q$
has varying rank. It is still not clear whether the exponential estimates we derive in this paper holds in this general context because our proof strongly relies on the existence of canonical model of neighborhoods of
![]() $Q$
. For this reason, we also impose Condition (3). We remark that Condition (3) means that the 2-form
$Q$
. For this reason, we also impose Condition (3). We remark that Condition (3) means that the 2-form
![]() $d\unicode[STIX]{x1D706}|_{Q}$
becomes a presymplectic form.
$d\unicode[STIX]{x1D706}|_{Q}$
becomes a presymplectic form.
Depending on the type of the presymplectic form, we say that
![]() $Q$
is of prequantization type if the rank of
$Q$
is of prequantization type if the rank of
![]() $d\unicode[STIX]{x1D706}|_{Q}$
is maximal, and is of isotropic type if the rank of
$d\unicode[STIX]{x1D706}|_{Q}$
is maximal, and is of isotropic type if the rank of
![]() $d\unicode[STIX]{x1D706}|_{Q}$
is zero. The general case is a mixture of these two. In particular when
$d\unicode[STIX]{x1D706}|_{Q}$
is zero. The general case is a mixture of these two. In particular when
![]() $\dim M=3$
, such
$\dim M=3$
, such
![]() $Q$
must be either of prequantization type or of isotropic type. This is the case dealt with in [Reference Hofer, Wysocki and ZehnderHWZ3]. The general case considered in [Reference BourgeoisBou], [Reference Bourgeois, Eliashberg, Hofer, Wysocki and ZehnderBEHWZ] includes the mixed type.
$Q$
must be either of prequantization type or of isotropic type. This is the case dealt with in [Reference Hofer, Wysocki and ZehnderHWZ3]. The general case considered in [Reference BourgeoisBou], [Reference Bourgeois, Eliashberg, Hofer, Wysocki and ZehnderBEHWZ] includes the mixed type.
Definition 1.3. (Precontact form)
We call one-form
![]() $\unicode[STIX]{x1D703}$
on a manifold
$\unicode[STIX]{x1D703}$
on a manifold
![]() $Q$
a precontact form if
$Q$
a precontact form if
![]() $d\unicode[STIX]{x1D703}$
has constant rank, that is, if
$d\unicode[STIX]{x1D703}$
has constant rank, that is, if
![]() $d\unicode[STIX]{x1D703}$
is a presymplectic form.
$d\unicode[STIX]{x1D703}$
is a presymplectic form.
While the notion of presymplectic manifolds is well established in symplectic geometry, this contact analogue seems to have not been used in literature, at least formally, as far as we know.
With this terminology introduced, we prove the following theorem.
Theorem 1.4. (Theorem 3.11)
Let
![]() $\unicode[STIX]{x1D706}$
be a Morse–Bott-type contact form of contact manifold
$\unicode[STIX]{x1D706}$
be a Morse–Bott-type contact form of contact manifold
![]() $(M,\unicode[STIX]{x1D709})$
as defined above. Let
$(M,\unicode[STIX]{x1D709})$
as defined above. Let
![]() $Q$
be an associated Morse–Bott submanifold of closed Reeb orbits. Suppose that
$Q$
be an associated Morse–Bott submanifold of closed Reeb orbits. Suppose that
![]() $Q$
is embedded and
$Q$
is embedded and
![]() $d\unicode[STIX]{x1D706}|_{Q}=i_{Q}^{\ast }(d\unicode[STIX]{x1D706})$
has constant rank. Then
$d\unicode[STIX]{x1D706}|_{Q}=i_{Q}^{\ast }(d\unicode[STIX]{x1D706})$
has constant rank. Then
![]() $Q$
carries:
$Q$
carries:
(1) a locally free
 $S^{1}$
-action generated by the Reeb vector field
$S^{1}$
-action generated by the Reeb vector field
 $X_{\unicode[STIX]{x1D706}}|_{Q}$
;
$X_{\unicode[STIX]{x1D706}}|_{Q}$
;(2) the precontact form
 $\unicode[STIX]{x1D703}$
given by
$\unicode[STIX]{x1D703}$
given by
 $\unicode[STIX]{x1D703}=i_{Q}^{\ast }\unicode[STIX]{x1D706}$
and the splitting (1.2)such that the distribution
$\unicode[STIX]{x1D703}=i_{Q}^{\ast }\unicode[STIX]{x1D706}$
and the splitting (1.2)such that the distribution $$\begin{eqnarray}\ker d\unicode[STIX]{x1D703}=\mathbb{R}\{X_{\unicode[STIX]{x1D703}}\}\oplus H,\end{eqnarray}$$
$$\begin{eqnarray}\ker d\unicode[STIX]{x1D703}=\mathbb{R}\{X_{\unicode[STIX]{x1D703}}\}\oplus H,\end{eqnarray}$$
 $H=\ker d\unicode[STIX]{x1D703}\cap \unicode[STIX]{x1D709}|_{Q}$
is integrable;
$H=\ker d\unicode[STIX]{x1D703}\cap \unicode[STIX]{x1D709}|_{Q}$
is integrable;(3) an
 $S^{1}$
-equivariant symplectic vector bundle
$S^{1}$
-equivariant symplectic vector bundle
 $(E,\unicode[STIX]{x1D6FA})\rightarrow Q$
with
$(E,\unicode[STIX]{x1D6FA})\rightarrow Q$
with  $$\begin{eqnarray}E=(TQ)^{d\unicode[STIX]{x1D706}}/\!\ker d\unicode[STIX]{x1D703},\qquad \unicode[STIX]{x1D6FA}=[d\unicode[STIX]{x1D706}]_{E}.\end{eqnarray}$$
$$\begin{eqnarray}E=(TQ)^{d\unicode[STIX]{x1D706}}/\!\ker d\unicode[STIX]{x1D703},\qquad \unicode[STIX]{x1D6FA}=[d\unicode[STIX]{x1D706}]_{E}.\end{eqnarray}$$
Here we use the fact that there exists a canonical embedding
and
![]() $d\unicode[STIX]{x1D706}|_{(TQ)^{d\unicode[STIX]{x1D706}}}$
canonically induces a bilinear form
$d\unicode[STIX]{x1D706}|_{(TQ)^{d\unicode[STIX]{x1D706}}}$
canonically induces a bilinear form
![]() $[d\unicode[STIX]{x1D706}]_{E}$
on
$[d\unicode[STIX]{x1D706}]_{E}$
on
![]() $E=(TQ)^{d\unicode[STIX]{x1D706}}/\ker di_{Q}^{\ast }\unicode[STIX]{x1D706}$
by symplectic reduction.
$E=(TQ)^{d\unicode[STIX]{x1D706}}/\ker di_{Q}^{\ast }\unicode[STIX]{x1D706}$
by symplectic reduction.
Definition 1.5. Let
![]() $(Q,\unicode[STIX]{x1D703})$
be a precontact manifold equipped with the splitting (1.2). We call such a triple
$(Q,\unicode[STIX]{x1D703})$
be a precontact manifold equipped with the splitting (1.2). We call such a triple
![]() $(Q,\unicode[STIX]{x1D703},H)$
a Morse–Bott contact setup.
$(Q,\unicode[STIX]{x1D703},H)$
a Morse–Bott contact setup.
Denote by
![]() ${\mathcal{F}}$
and
${\mathcal{F}}$
and
![]() ${\mathcal{N}}$
the foliations associated to the distribution
${\mathcal{N}}$
the foliations associated to the distribution
![]() $\ker d\unicode[STIX]{x1D703}$
and
$\ker d\unicode[STIX]{x1D703}$
and
![]() $H$
, respectively. We also denote by
$H$
, respectively. We also denote by
![]() $T{\mathcal{F}}$
,
$T{\mathcal{F}}$
,
![]() $T{\mathcal{N}}$
the associated foliation tangent bundles and
$T{\mathcal{N}}$
the associated foliation tangent bundles and
![]() $T^{\ast }{\mathcal{N}}$
the foliation cotangent bundle of
$T^{\ast }{\mathcal{N}}$
the foliation cotangent bundle of
![]() ${\mathcal{N}}$
.
${\mathcal{N}}$
.
We prove the following canonical model theorem which describes a natural way of thickening of Morse–Bott contact setup
![]() $(Q,\unicode[STIX]{x1D703},H)$
whenever a symplectic vector bundle
$(Q,\unicode[STIX]{x1D703},H)$
whenever a symplectic vector bundle
![]() $E\rightarrow Q$
is given.
$E\rightarrow Q$
is given.
Theorem 1.6. Let
![]() $(Q,\unicode[STIX]{x1D703},H)$
be a Morse–Bott contact setup. Let a symplectic vector bundle
$(Q,\unicode[STIX]{x1D703},H)$
be a Morse–Bott contact setup. Let a symplectic vector bundle
![]() $(E,\unicode[STIX]{x1D6FA})\rightarrow Q$
be given. Then the bundle
$(E,\unicode[STIX]{x1D6FA})\rightarrow Q$
be given. Then the bundle
![]() $F=T^{\ast }{\mathcal{N}}\oplus E$
carries a canonical contact form
$F=T^{\ast }{\mathcal{N}}\oplus E$
carries a canonical contact form
![]() $\unicode[STIX]{x1D706}_{F;G}$
defined as in (4.8), for each choice of complement
$\unicode[STIX]{x1D706}_{F;G}$
defined as in (4.8), for each choice of complement
![]() $G$
such that
$G$
such that
![]() $TQ=T{\mathcal{F}}\oplus G$
. Furthermore, for two such choices of
$TQ=T{\mathcal{F}}\oplus G$
. Furthermore, for two such choices of
![]() $G$
,
$G$
,
![]() $G^{\prime }$
, two induced contact structures are naturally isomorphic.
$G^{\prime }$
, two induced contact structures are naturally isomorphic.
Based on this theorem, we denote any such
![]() $\unicode[STIX]{x1D706}_{F;G}$
just by
$\unicode[STIX]{x1D706}_{F;G}$
just by
![]() $\unicode[STIX]{x1D706}_{F}$
suppressing
$\unicode[STIX]{x1D706}_{F}$
suppressing
![]() $G$
from its notation. This normal form provides a general class of contact manifolds equipped with a contact form of Morse–Bott type.
$G$
from its notation. This normal form provides a general class of contact manifolds equipped with a contact form of Morse–Bott type.
Finally we prove the following canonical neighborhood theorem for
![]() $Q\subset M$
with
$Q\subset M$
with
![]() $Q$
defined above for any Morse–Bott contact form
$Q$
defined above for any Morse–Bott contact form
![]() $\unicode[STIX]{x1D706}$
of contact manifold
$\unicode[STIX]{x1D706}$
of contact manifold
![]() $(M,\unicode[STIX]{x1D709})$
.
$(M,\unicode[STIX]{x1D709})$
.
Theorem 1.7. (Theorem 5.1)
Let
![]() $Q$
be the submanifold foliated by closed Reeb orbits of Morse–Bott-type contact form
$Q$
be the submanifold foliated by closed Reeb orbits of Morse–Bott-type contact form
![]() $\unicode[STIX]{x1D706}$
of contact manifold
$\unicode[STIX]{x1D706}$
of contact manifold
![]() $(M,\unicode[STIX]{x1D709})$
, and
$(M,\unicode[STIX]{x1D709})$
, and
![]() $(Q,\unicode[STIX]{x1D703})$
and
$(Q,\unicode[STIX]{x1D703})$
and
![]() $(E,\unicode[STIX]{x1D6FA})$
be the associated pair defined above. Let
$(E,\unicode[STIX]{x1D6FA})$
be the associated pair defined above. Let
![]() $(F,\unicode[STIX]{x1D706}_{F})$
be the model contact manifold with
$(F,\unicode[STIX]{x1D706}_{F})$
be the model contact manifold with
![]() $F=T^{\ast }{\mathcal{N}}\oplus E$
and
$F=T^{\ast }{\mathcal{N}}\oplus E$
and
![]() $\unicode[STIX]{x1D706}_{F}$
be the contact form on
$\unicode[STIX]{x1D706}_{F}$
be the contact form on
![]() $U_{F}\subset F$
given in (4.8).
$U_{F}\subset F$
given in (4.8).
Then there exist neighborhoods
![]() ${\mathcal{U}}$
of
${\mathcal{U}}$
of
![]() $Q$
and
$Q$
and
![]() $U_{F}$
of the zero section
$U_{F}$
of the zero section
![]() $o_{F}$
and a diffeomorphism
$o_{F}$
and a diffeomorphism
![]() $\unicode[STIX]{x1D713}:U_{F}\rightarrow {\mathcal{U}}$
and a function
$\unicode[STIX]{x1D713}:U_{F}\rightarrow {\mathcal{U}}$
and a function
![]() $f:U_{F}\rightarrow \mathbb{R}$
such that
$f:U_{F}\rightarrow \mathbb{R}$
such that
and
where we use the canonical identification of
![]() $VTF|_{o_{F}}\cong T^{\ast }{\mathcal{N}}\oplus E$
on the zero section
$VTF|_{o_{F}}\cong T^{\ast }{\mathcal{N}}\oplus E$
on the zero section
![]() $o_{F}\cong Q$
.
$o_{F}\cong Q$
.
Remark 1.8. We would like to remark that while the bundles
![]() $E$
and
$E$
and
![]() $TQ/T{\mathcal{F}}$
carry canonical fiberwise symplectic form and so carry canonical orientations induced by
$TQ/T{\mathcal{F}}$
carry canonical fiberwise symplectic form and so carry canonical orientations induced by
![]() $d\unicode[STIX]{x1D706}$
, the bundle
$d\unicode[STIX]{x1D706}$
, the bundle
![]() $T{\mathcal{N}}$
may not be orientable in general along a Reeb orbit corresponding to an orbifold point in
$T{\mathcal{N}}$
may not be orientable in general along a Reeb orbit corresponding to an orbifold point in
![]() $P=Q/\sim$
.
$P=Q/\sim$
.
1.2 The three-interval method of exponential estimates
For the study of the asymptotic behavior of finite
![]() $\unicode[STIX]{x1D70B}$
-energy solutions of contact instanton
$\unicode[STIX]{x1D70B}$
-energy solutions of contact instanton
![]() $w:\dot{\unicode[STIX]{x1D6F4}}\rightarrow M$
near a Morse–Bott submanifold
$w:\dot{\unicode[STIX]{x1D6F4}}\rightarrow M$
near a Morse–Bott submanifold
![]() $Q$
, we introduce the following class of
$Q$
, we introduce the following class of
![]() $CR$
-almost complex structures.
$CR$
-almost complex structures.
Definition 1.9. (Definition 8.2)
Let
![]() $Q\subset M$
be a Morse–Bott submanifold foliated by closed Reeb orbits of
$Q\subset M$
be a Morse–Bott submanifold foliated by closed Reeb orbits of
![]() $\unicode[STIX]{x1D706}$
. Suppose
$\unicode[STIX]{x1D706}$
. Suppose
![]() $J$
defines a contact triad
$J$
defines a contact triad
![]() $(M,\unicode[STIX]{x1D706},J)$
. We say a
$(M,\unicode[STIX]{x1D706},J)$
. We say a
![]() $CR$
-almost complex structure
$CR$
-almost complex structure
![]() $J$
for
$J$
for
![]() $(M,\unicode[STIX]{x1D709})$
is adapted to the submanifold
$(M,\unicode[STIX]{x1D709})$
is adapted to the submanifold
![]() $Q$
or simply is
$Q$
or simply is
![]() $Q$
-adapted if
$Q$
-adapted if
![]() $J$
satisfies
$J$
satisfies
Note that this condition is vacuous for the nondegenerate case, but for the general Morse–Bott case, the class of adapted
![]() $J$
is strictly smaller than the one of general
$J$
is strictly smaller than the one of general
![]() $CR$
-almost complex structures of the triad. The set of
$CR$
-almost complex structures of the triad. The set of
![]() $Q$
-adapted
$Q$
-adapted
![]() $J$
’s is contractible and the proof is given in Appendix A. As far as the applications to contact topology are concerned, requiring this condition is not any restriction but seems to be necessary for the analysis of contact-instanton maps or of the pseudoholomorphic maps in the symplectization (or in the symplectic manifolds with contact-type boundary).
$J$
’s is contractible and the proof is given in Appendix A. As far as the applications to contact topology are concerned, requiring this condition is not any restriction but seems to be necessary for the analysis of contact-instanton maps or of the pseudoholomorphic maps in the symplectization (or in the symplectic manifolds with contact-type boundary).
Let
![]() $w:\dot{\unicode[STIX]{x1D6F4}}\rightarrow M$
be a contact-instanton map, that is, satisfying (1.1) at a cylindrical end
$w:\dot{\unicode[STIX]{x1D6F4}}\rightarrow M$
be a contact-instanton map, that is, satisfying (1.1) at a cylindrical end
![]() $[0,\infty )\times S^{1}$
, which now can be written as
$[0,\infty )\times S^{1}$
, which now can be written as
for
![]() $(\unicode[STIX]{x1D70F},t)\in [0,\infty )\times S^{1}$
. We put the following basic hypotheses for the study of exponential convergence.
$(\unicode[STIX]{x1D70F},t)\in [0,\infty )\times S^{1}$
. We put the following basic hypotheses for the study of exponential convergence.
Hypothesis 1.10. (Hypothesis 9.1)
(1) Finite
 $\unicode[STIX]{x1D70B}$
-energy:
$\unicode[STIX]{x1D70B}$
-energy:
 $E^{\unicode[STIX]{x1D70B}}(w):=(1/2)\int _{[0,\infty )\times S^{1}}|d^{\unicode[STIX]{x1D70B}}w|^{2}<\infty$
;
$E^{\unicode[STIX]{x1D70B}}(w):=(1/2)\int _{[0,\infty )\times S^{1}}|d^{\unicode[STIX]{x1D70B}}w|^{2}<\infty$
;(2) finite derivative bound:
 $\Vert dw\Vert _{C^{0}([0,\infty )\times S^{1})}\leqslant C<\infty$
;
$\Vert dw\Vert _{C^{0}([0,\infty )\times S^{1})}\leqslant C<\infty$
;(3) nonvanishing asymptotic action:
 $$\begin{eqnarray}{\mathcal{T}}:=\frac{1}{2}\int _{[0,\infty )\times S^{1}}|d^{\unicode[STIX]{x1D70B}}w|^{2}+\int _{\{0\}\times S^{1}}(w|_{\{0\}\times S^{1}})^{\ast }\unicode[STIX]{x1D706}\neq 0;\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{T}}:=\frac{1}{2}\int _{[0,\infty )\times S^{1}}|d^{\unicode[STIX]{x1D70B}}w|^{2}+\int _{\{0\}\times S^{1}}(w|_{\{0\}\times S^{1}})^{\ast }\unicode[STIX]{x1D706}\neq 0;\end{eqnarray}$$
(4) vanishing asymptotic charge:
 ${\mathcal{Q}}:=\int _{\{0\}\times S^{1}}((w|_{\{0\}\times S^{1}})^{\ast }\unicode[STIX]{x1D706}\circ j)=0$
.
${\mathcal{Q}}:=\int _{\{0\}\times S^{1}}((w|_{\{0\}\times S^{1}})^{\ast }\unicode[STIX]{x1D706}\circ j)=0$
.
Under these hypotheses, we establish the following
![]() $C^{\infty }$
uniform exponential convergence of
$C^{\infty }$
uniform exponential convergence of
![]() $w$
to a closed Reeb orbit
$w$
to a closed Reeb orbit
![]() $z$
of period
$z$
of period
![]() $T={\mathcal{T}}$
. This result was already known in [Reference Hofer, Wysocki and ZehnderHWZ3, Reference BourgeoisBou, Reference BaoBa] in the context of pseudoholomorphic curves
$T={\mathcal{T}}$
. This result was already known in [Reference Hofer, Wysocki and ZehnderHWZ3, Reference BourgeoisBou, Reference BaoBa] in the context of pseudoholomorphic curves
![]() $u=(w,a)$
in symplectizations. However, we emphasize that our proof presented here, which uses the three-interval framework, is different from the ones [Reference Hofer, Wysocki and ZehnderHWZ3, Reference BourgeoisBou, Reference BaoBa] even in the symplectization case. Furthermore, when we deal with the case of symplectization, our method completely separates the estimates of
$u=(w,a)$
in symplectizations. However, we emphasize that our proof presented here, which uses the three-interval framework, is different from the ones [Reference Hofer, Wysocki and ZehnderHWZ3, Reference BourgeoisBou, Reference BaoBa] even in the symplectization case. Furthermore, when we deal with the case of symplectization, our method completely separates the estimates of
![]() $w$
from that of
$w$
from that of
![]() $a$
’s. (See Section 13.)
$a$
’s. (See Section 13.)
Theorem 1.11. Assume
![]() $(M,\unicode[STIX]{x1D706})$
is a Morse–Bott contact manifold and
$(M,\unicode[STIX]{x1D706})$
is a Morse–Bott contact manifold and
![]() $w$
is a contact instanton satisfying the Hypothesis 1.10 at the given end. Then there exists a closed Reeb orbit
$w$
is a contact instanton satisfying the Hypothesis 1.10 at the given end. Then there exists a closed Reeb orbit
![]() $z$
with period
$z$
with period
![]() $T={\mathcal{T}}$
and positive constant
$T={\mathcal{T}}$
and positive constant
![]() $\unicode[STIX]{x1D6FF}$
determined by
$\unicode[STIX]{x1D6FF}$
determined by
![]() $z$
, such that
$z$
, such that
and
 $$\begin{eqnarray}\displaystyle & & \displaystyle \left\Vert \unicode[STIX]{x1D70B}\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D70F},\cdot )\right\Vert _{C^{0}(S^{1})}<Ce^{-\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70F}},\qquad \left\Vert \unicode[STIX]{x1D70B}\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}t}(\unicode[STIX]{x1D70F},\cdot )\right\Vert _{C^{0}(S^{1})}<Ce^{-\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70F}}\nonumber\\ \displaystyle & & \displaystyle \left\Vert \unicode[STIX]{x1D706}\left(\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}\right)(\unicode[STIX]{x1D70F},\cdot )\right\Vert _{C^{0}(S^{1})}<Ce^{-\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70F}},\qquad \left\Vert \unicode[STIX]{x1D706}\left(\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}t}\right)(\unicode[STIX]{x1D70F},\cdot )-T\right\Vert _{C^{0}(S^{1})}<Ce^{-\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70F}}\nonumber\\ \displaystyle & & \displaystyle \Vert \unicode[STIX]{x1D6FB}^{l}dw(\unicode[STIX]{x1D70F},t)\Vert _{C^{0}(S^{1})}<C_{l}e^{-\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70F}}\quad \text{for any}~l\geqslant 1,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \left\Vert \unicode[STIX]{x1D70B}\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D70F},\cdot )\right\Vert _{C^{0}(S^{1})}<Ce^{-\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70F}},\qquad \left\Vert \unicode[STIX]{x1D70B}\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}t}(\unicode[STIX]{x1D70F},\cdot )\right\Vert _{C^{0}(S^{1})}<Ce^{-\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70F}}\nonumber\\ \displaystyle & & \displaystyle \left\Vert \unicode[STIX]{x1D706}\left(\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}\right)(\unicode[STIX]{x1D70F},\cdot )\right\Vert _{C^{0}(S^{1})}<Ce^{-\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70F}},\qquad \left\Vert \unicode[STIX]{x1D706}\left(\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}t}\right)(\unicode[STIX]{x1D70F},\cdot )-T\right\Vert _{C^{0}(S^{1})}<Ce^{-\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70F}}\nonumber\\ \displaystyle & & \displaystyle \Vert \unicode[STIX]{x1D6FB}^{l}dw(\unicode[STIX]{x1D70F},t)\Vert _{C^{0}(S^{1})}<C_{l}e^{-\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70F}}\quad \text{for any}~l\geqslant 1,\nonumber\end{eqnarray}$$
where
![]() $d$
is the distance function induced from the triad metric on
$d$
is the distance function induced from the triad metric on
![]() $M$
and
$M$
and
![]() $C$
,
$C$
,
![]() $C_{l}$
are positive constants which only depend on
$C_{l}$
are positive constants which only depend on
![]() $l$
.
$l$
.
Now comes the outline of the strategy of our proof of exponential convergence in the present paper. Mundet i Riera and Tian in [Reference Mundet i Riera and TianMT] elegantly used a discrete method of three-interval arguments in proving exponential decay under the assumption of
![]() $C^{0}$
-convergence already established. However, for most cases of interests, the
$C^{0}$
-convergence already established. However, for most cases of interests, the
![]() $C^{0}$
-convergence is not a priori given in the beginning but it is often the case that the
$C^{0}$
-convergence is not a priori given in the beginning but it is often the case that the
![]() $C^{0}$
-convergence can be obtained only after one proves the exponential convergence of derivatives. (See the proofs of, for example, [Reference Hofer, Wysocki and ZehnderHWZ1, Reference Hofer, Wysocki and ZehnderHWZ2, Reference Hofer, Wysocki and ZehnderHWZ4], [Reference Hofer, Wysocki and ZehnderHWZ3], [Reference BourgeoisBou], [Reference BaoBa].) To obtain the exponential estimates of derivatives, researchers conduct some brute-force calculations in deriving the needed differential inequality, and then proceed from there toward the final result. Such calculations, especially in coordinates, become quite complicated for the Morse–Bott situation and hide the geometry that explains why such a differential inequality could be expected.
$C^{0}$
-convergence can be obtained only after one proves the exponential convergence of derivatives. (See the proofs of, for example, [Reference Hofer, Wysocki and ZehnderHWZ1, Reference Hofer, Wysocki and ZehnderHWZ2, Reference Hofer, Wysocki and ZehnderHWZ4], [Reference Hofer, Wysocki and ZehnderHWZ3], [Reference BourgeoisBou], [Reference BaoBa].) To obtain the exponential estimates of derivatives, researchers conduct some brute-force calculations in deriving the needed differential inequality, and then proceed from there toward the final result. Such calculations, especially in coordinates, become quite complicated for the Morse–Bott situation and hide the geometry that explains why such a differential inequality could be expected.
Our proof is divided into two parts by writing
![]() $w=(u,s)$
in the normalized contact triad
$w=(u,s)$
in the normalized contact triad
![]() $(U_{F},\unicode[STIX]{x1D706}_{F},J_{0})$
(see Definition 8.7) with
$(U_{F},\unicode[STIX]{x1D706}_{F},J_{0})$
(see Definition 8.7) with
![]() $U_{F}\subset F\rightarrow Q$
for any given compatible
$U_{F}\subset F\rightarrow Q$
for any given compatible
![]() $J$
adapted to
$J$
adapted to
![]() $Q$
, where
$Q$
, where
![]() $J_{0}$
is canonical normalized
$J_{0}$
is canonical normalized
![]() $CR$
-almost complex structure associated to
$CR$
-almost complex structure associated to
![]() $J$
. We also decompose
$J$
. We also decompose
![]() $s=(\unicode[STIX]{x1D707},e)$
in terms of the splitting
$s=(\unicode[STIX]{x1D707},e)$
in terms of the splitting
![]() $F=T^{\ast }{\mathcal{N}}\oplus E$
. In this decomposition, the
$F=T^{\ast }{\mathcal{N}}\oplus E$
. In this decomposition, the
![]() $L^{2}$
-exponential estimates for the
$L^{2}$
-exponential estimates for the
![]() $e$
-component is an easy consequence of the three-interval method which we formulate above in a general abstract framework (see Theorem 10.11 for the precise statement). This estimate belongs to the standard realm of exponential decay proof for the asymptotically cylindrical elliptic equations.
$e$
-component is an easy consequence of the three-interval method which we formulate above in a general abstract framework (see Theorem 10.11 for the precise statement). This estimate belongs to the standard realm of exponential decay proof for the asymptotically cylindrical elliptic equations.
However, the study of
![]() $L^{2}$
-exponential estimates for
$L^{2}$
-exponential estimates for
![]() $(u,\unicode[STIX]{x1D707})$
does not directly belong to this standard realm. Although we still apply similar three-interval method for the study of
$(u,\unicode[STIX]{x1D707})$
does not directly belong to this standard realm. Although we still apply similar three-interval method for the study of
![]() $L^{2}$
-exponential convergence, its study is much more subtle than that of the normal component due to the presence of nontrivial kernel of the asymptotic operator
$L^{2}$
-exponential convergence, its study is much more subtle than that of the normal component due to the presence of nontrivial kernel of the asymptotic operator
![]() $B_{\infty }$
of the linearization. To handle the
$B_{\infty }$
of the linearization. To handle the
![]() $(u,\unicode[STIX]{x1D707})$
-component, we formulate the following general theorem from the abstract framework of the three-interval argument, and refer readers to Sections 10, 11.3 for the precise statement and its proof.
$(u,\unicode[STIX]{x1D707})$
-component, we formulate the following general theorem from the abstract framework of the three-interval argument, and refer readers to Sections 10, 11.3 for the precise statement and its proof.
Theorem 1.12. Assume
![]() $\unicode[STIX]{x1D709}(\unicode[STIX]{x1D70F},t)$
is a section of some vector bundle on
$\unicode[STIX]{x1D709}(\unicode[STIX]{x1D70F},t)$
is a section of some vector bundle on
![]() $\mathbb{R}\times S^{1}$
which satisfies the equation
$\mathbb{R}\times S^{1}$
which satisfies the equation
of Cauchy–Riemann type (or more generally any elliptic PDE of evolution type), where
![]() $S$
is a bounded symmetric operator.
$S$
is a bounded symmetric operator.
Suppose that there exists a sequence
![]() $\{\bar{\unicode[STIX]{x1D701}}_{k}\}$
(e.g., by performing a suitable rescaling of
$\{\bar{\unicode[STIX]{x1D701}}_{k}\}$
(e.g., by performing a suitable rescaling of
![]() $\unicode[STIX]{x1D701}$
) such that at least one subsequence converges to a nonzero section
$\unicode[STIX]{x1D701}$
) such that at least one subsequence converges to a nonzero section
![]() $\bar{\unicode[STIX]{x1D701}}_{\infty }$
of a (trivial) Banach bundle over a fixed finite interval, say on
$\bar{\unicode[STIX]{x1D701}}_{\infty }$
of a (trivial) Banach bundle over a fixed finite interval, say on
![]() $[0,3]$
, that satisfies the ODE
$[0,3]$
, that satisfies the ODE
on the associated Banach space.
Then provided
![]() $\Vert \unicode[STIX]{x1D701}(\unicode[STIX]{x1D70F},\cdot )\Vert _{L^{2}(S^{1})}$
converges to zero as
$\Vert \unicode[STIX]{x1D701}(\unicode[STIX]{x1D70F},\cdot )\Vert _{L^{2}(S^{1})}$
converges to zero as
![]() $\unicode[STIX]{x1D70F}$
goes to
$\unicode[STIX]{x1D70F}$
goes to
![]() $\infty$
,
$\infty$
,
![]() $\Vert \unicode[STIX]{x1D701}(\unicode[STIX]{x1D70F},\cdot )\Vert _{L^{2}(S^{1})}$
decays exponentially fast with the rate
$\Vert \unicode[STIX]{x1D701}(\unicode[STIX]{x1D70F},\cdot )\Vert _{L^{2}(S^{1})}$
decays exponentially fast with the rate
![]() $\unicode[STIX]{x1D6FF}>0$
for any constant
$\unicode[STIX]{x1D6FF}>0$
for any constant
![]() $\unicode[STIX]{x1D6FF}<\min \{\unicode[STIX]{x1D706}_{0},\unicode[STIX]{x1D6FF}_{0}\}$
where
$\unicode[STIX]{x1D6FF}<\min \{\unicode[STIX]{x1D706}_{0},\unicode[STIX]{x1D6FF}_{0}\}$
where
![]() $\unicode[STIX]{x1D706}_{0}$
is the smallest absolute value of nonzero eigenvalues of
$\unicode[STIX]{x1D706}_{0}$
is the smallest absolute value of nonzero eigenvalues of
![]() $B_{\infty }$
.
$B_{\infty }$
.
Remark 1.13. For the special case when
![]() $B_{\infty }$
has only trivial kernel, the result can be regarded as the discrete analogue of the differential inequality method used by Robbin and Salamon in [Reference Robbin and SalamonRS].
$B_{\infty }$
has only trivial kernel, the result can be regarded as the discrete analogue of the differential inequality method used by Robbin and Salamon in [Reference Robbin and SalamonRS].
In this framework, our exponential convergence proof is based on intrinsic geometric tensor calculations which is coordinate-free. As a result, our proof make it manifest that (roughly) the exponential decay occurs whenever the geometric PDE has bounded energy at cylindrical ends and the limiting equation is of linear evolution type
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x1D701}}_{\infty }/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}+B_{\infty }\overline{\unicode[STIX]{x1D701}}_{\infty }=0$
, where
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x1D701}}_{\infty }/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}+B_{\infty }\overline{\unicode[STIX]{x1D701}}_{\infty }=0$
, where
![]() $B_{\infty }$
is an elliptic operator with discrete spectrum. If
$B_{\infty }$
is an elliptic operator with discrete spectrum. If
![]() $B_{\infty }$
has trivial kernel, the conclusion follows rather immediately from the three-interval argument. Even when
$B_{\infty }$
has trivial kernel, the conclusion follows rather immediately from the three-interval argument. Even when
![]() $B_{\infty }$
contains nontrivial kernel, the exponential decay would still follow as long as some geometric condition, like the Morse–Bott assumption in the current case of our interest, enables one to extract some nonvanishing solution of the limit equation
$B_{\infty }$
contains nontrivial kernel, the exponential decay would still follow as long as some geometric condition, like the Morse–Bott assumption in the current case of our interest, enables one to extract some nonvanishing solution of the limit equation
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x1D701}}_{\infty }/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}+B_{\infty }\overline{\unicode[STIX]{x1D701}}_{\infty }=0$
that arises in the course of three-interval arguments. Moreover, the decay rate
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x1D701}}_{\infty }/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}+B_{\infty }\overline{\unicode[STIX]{x1D701}}_{\infty }=0$
that arises in the course of three-interval arguments. Moreover, the decay rate
![]() $\unicode[STIX]{x1D6FF}>0$
is always provided by the minimal eigenvalue of
$\unicode[STIX]{x1D6FF}>0$
is always provided by the minimal eigenvalue of
![]() $B_{\infty }$
.
$B_{\infty }$
.
Now we roughly explain how the nonvanishing limiting solution mentioned above is obtained in the current situation: first, the canonical neighborhood provided in Part 1 is used to split the contact-instanton equations into the vertical and horizontal parts. By this way, only the horizontal equation could be involved with the kernel of
![]() $B_{\infty }$
which by the Morse–Bott condition has nice geometric structure in the sense that the kernel can be excluded by looking at a higher derivative instead of the map itself. Then, to further see the limit of the derivative is indeed nonvanishing, we apply the geometric decomposition to the derivative and study the center of mass on the Morse–Bott submanifold
$B_{\infty }$
which by the Morse–Bott condition has nice geometric structure in the sense that the kernel can be excluded by looking at a higher derivative instead of the map itself. Then, to further see the limit of the derivative is indeed nonvanishing, we apply the geometric decomposition to the derivative and study the center of mass on the Morse–Bott submanifold
![]() $Q$
. The details are presented in Sections 11.3 and 11.4.
$Q$
. The details are presented in Sections 11.3 and 11.4.
Part 1 Contact Hamiltonian geometry and canonical neighborhoods
The main purpose of this part is to prove a canonical neighborhood theorem for the loci of closed Reeb orbits when the contact form
![]() $\unicode[STIX]{x1D706}$
of a contact manifold
$\unicode[STIX]{x1D706}$
of a contact manifold
![]() $(M,\unicode[STIX]{x1D709})$
is of Morse–Bott type. The results of this part provides geometric preparation for the study of asymptotic exponential convergence of contact instanton at a puncture of the domain Riemann surface.
$(M,\unicode[STIX]{x1D709})$
is of Morse–Bott type. The results of this part provides geometric preparation for the study of asymptotic exponential convergence of contact instanton at a puncture of the domain Riemann surface.
The outline of Part 1 in sectionwise is as follows.
∙ In Section 2, we review some basic facts related to contact forms of a contact manifold. We first set up a natural isomorphism between
 $TM$
and
$TM$
and
 $T^{\ast }M$
using the contact form
$T^{\ast }M$
using the contact form
 $\unicode[STIX]{x1D706}$
. This is a contact analogue of the isomorphism between tangent bundle and cotangent bundle for symplectic manifolds. Then we derive explicit formulas of the Reeb vector field
$\unicode[STIX]{x1D706}$
. This is a contact analogue of the isomorphism between tangent bundle and cotangent bundle for symplectic manifolds. Then we derive explicit formulas of the Reeb vector field
 $R_{f\unicode[STIX]{x1D706}}$
and the contact projection
$R_{f\unicode[STIX]{x1D706}}$
and the contact projection
 $\unicode[STIX]{x1D70B}_{f\unicode[STIX]{x1D706}}$
in terms of
$\unicode[STIX]{x1D70B}_{f\unicode[STIX]{x1D706}}$
in terms of
 $X_{\unicode[STIX]{x1D706}}$
,
$X_{\unicode[STIX]{x1D706}}$
,
 $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}$
and
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}$
and
 $f$
, respectively.
$f$
, respectively.∙ In Section 3, we introduce the definition of Morse–Bott contact forms. Then we study the canonical precontact structure associated to the loci of closed Reeb orbits under Morse–Bott assumption.
∙ In Section 4, we introduce the notion of contact thickening of precontact structure. It is the contact analogue of the symplectic thickening for presymplectic structure constructed in [Reference GotayG], [Reference Oh and ParkOP].
∙ In Section 5, we prove a canonical neighborhood theorem of the loci of closed Reeb orbits
 $Q$
under the Morse–Bott assumption.
$Q$
under the Morse–Bott assumption.∙ In Section 6, we derive the linearization formula of a Reeb orbit in the normal form.
∙ In Section 7, we express the derivative
 $dw=(du,\unicode[STIX]{x1D6FB}_{du}f)$
of any smooth map
$dw=(du,\unicode[STIX]{x1D6FB}_{du}f)$
of any smooth map
 $w=(u,f)$
from a (punctured) surface into the normal neighborhood
$w=(u,f)$
from a (punctured) surface into the normal neighborhood
 $F$
of
$F$
of
 $Q$
in terms of the splitting
$Q$
in terms of the splitting  $$\begin{eqnarray}TU_{F}=TQ\oplus F=TQ\oplus (E\oplus JT{\mathcal{F}}),\quad TQ=T{\mathcal{F}}\oplus G.\end{eqnarray}$$
$$\begin{eqnarray}TU_{F}=TQ\oplus F=TQ\oplus (E\oplus JT{\mathcal{F}}),\quad TQ=T{\mathcal{F}}\oplus G.\end{eqnarray}$$
∙ In Sections 8 and 9, we introduce the class of adapted CR-almost complex structure and prove its abundance.
2 Basics on contact forms
We recall some basic facts on the contact geometry and contact Hamiltonian dynamics especially in relation to the perturbation of contact forms for a given contact manifold
![]() $(M,\unicode[STIX]{x1D709})$
.
$(M,\unicode[STIX]{x1D709})$
.
2.1
 $\unicode[STIX]{x1D706}$
-dual vector fields and
$\unicode[STIX]{x1D706}$
-dual vector fields and
 $\unicode[STIX]{x1D706}$
-dual one-forms
$\unicode[STIX]{x1D706}$
-dual one-forms
Let
![]() $(M,\unicode[STIX]{x1D709})$
be a contact manifold and
$(M,\unicode[STIX]{x1D709})$
be a contact manifold and
![]() $\unicode[STIX]{x1D706}$
be a contact form with
$\unicode[STIX]{x1D706}$
be a contact form with
![]() $\ker \unicode[STIX]{x1D706}=\unicode[STIX]{x1D709}$
. Consider its associated decomposition
$\ker \unicode[STIX]{x1D706}=\unicode[STIX]{x1D709}$
. Consider its associated decomposition
and denote by
![]() $\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}:TM\rightarrow \unicode[STIX]{x1D709}$
the associated projection. This decomposition canonically induces the corresponding dual decomposition
$\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}:TM\rightarrow \unicode[STIX]{x1D709}$
the associated projection. This decomposition canonically induces the corresponding dual decomposition
where
![]() $(\cdot )^{\bot }$
is the annihilator of
$(\cdot )^{\bot }$
is the annihilator of
![]() $(\cdot )$
. This gives rise to a decomposition
$(\cdot )$
. This gives rise to a decomposition
Then we have the following general lemma whose proof immediately follows from (2.2).
Lemma 2.1. For any given one-form
![]() $\unicode[STIX]{x1D6FC}$
, there exists a unique
$\unicode[STIX]{x1D6FC}$
, there exists a unique
![]() $Y_{\unicode[STIX]{x1D6FC}}\in \unicode[STIX]{x1D709}$
such that
$Y_{\unicode[STIX]{x1D6FC}}\in \unicode[STIX]{x1D709}$
such that
Definition 2.2. (
 $\unicode[STIX]{x1D706}$
-Dual vector field and one-form)
$\unicode[STIX]{x1D706}$
-Dual vector field and one-form)
Let
![]() $\unicode[STIX]{x1D706}$
be a given contact form of
$\unicode[STIX]{x1D706}$
be a given contact form of
![]() $(M,\unicode[STIX]{x1D709})$
. We define the
$(M,\unicode[STIX]{x1D709})$
. We define the
![]() $\unicode[STIX]{x1D706}$
-dual vector field of a one-form
$\unicode[STIX]{x1D706}$
-dual vector field of a one-form
![]() $\unicode[STIX]{x1D6FC}$
to be
$\unicode[STIX]{x1D6FC}$
to be
Conversely for any given vector field
![]() $X$
we define its
$X$
we define its
![]() $\unicode[STIX]{x1D706}$
-dual one-form by
$\unicode[STIX]{x1D706}$
-dual one-form by
For the simplicity of notation, we denote
![]() $\unicode[STIX]{x1D6FC}_{X}:=\sharp _{\unicode[STIX]{x1D706}}(X)$
. By definition, we have the identity
$\unicode[STIX]{x1D6FC}_{X}:=\sharp _{\unicode[STIX]{x1D706}}(X)$
. By definition, we have the identity
The following proposition is immediate from the definitions of the dual vector field and the dual one-forms.
Proposition 2.3. The map
![]() $\flat _{\unicode[STIX]{x1D706}}:\unicode[STIX]{x1D6FA}^{1}(M)\rightarrow \mathfrak{X}(M)$
,
$\flat _{\unicode[STIX]{x1D706}}:\unicode[STIX]{x1D6FA}^{1}(M)\rightarrow \mathfrak{X}(M)$
,
![]() $\unicode[STIX]{x1D6FC}\mapsto \flat _{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D6FC})$
and the map
$\unicode[STIX]{x1D6FC}\mapsto \flat _{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D6FC})$
and the map
![]() $\sharp ^{\unicode[STIX]{x1D706}}:\mathfrak{X}(M)\rightarrow \unicode[STIX]{x1D6FA}^{1}(M)$
,
$\sharp ^{\unicode[STIX]{x1D706}}:\mathfrak{X}(M)\rightarrow \unicode[STIX]{x1D6FA}^{1}(M)$
,
![]() $X\mapsto \unicode[STIX]{x1D6FC}_{X}$
are inverse to each other. In particular any vector field can be written as
$X\mapsto \unicode[STIX]{x1D6FC}_{X}$
are inverse to each other. In particular any vector field can be written as
![]() $\flat _{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D6FC})$
for a unique one-form
$\flat _{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D6FC})$
for a unique one-form
![]() $\unicode[STIX]{x1D6FC}$
and any one-form can be written as
$\unicode[STIX]{x1D6FC}$
and any one-form can be written as
![]() $\unicode[STIX]{x1D6FC}_{X}$
for a unique vector field
$\unicode[STIX]{x1D6FC}_{X}$
for a unique vector field
![]() $X$
.
$X$
.
By definition, we have
![]() $\flat _{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D706})=X_{\unicode[STIX]{x1D706}}$
which corresponds to the
$\flat _{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D706})=X_{\unicode[STIX]{x1D706}}$
which corresponds to the
![]() $\unicode[STIX]{x1D706}$
-dual to the contact form
$\unicode[STIX]{x1D706}$
-dual to the contact form
![]() $\unicode[STIX]{x1D706}$
itself for which
$\unicode[STIX]{x1D706}$
itself for which
![]() $Y_{\unicode[STIX]{x1D706}}=0$
by definition. Obviously when an exact one-form
$Y_{\unicode[STIX]{x1D706}}=0$
by definition. Obviously when an exact one-form
![]() $\unicode[STIX]{x1D6FC}$
is given, the choice of
$\unicode[STIX]{x1D6FC}$
is given, the choice of
![]() $h$
with
$h$
with
![]() $\unicode[STIX]{x1D6FC}=dh$
is unique modulo addition by a constant (on each connected component of
$\unicode[STIX]{x1D6FC}=dh$
is unique modulo addition by a constant (on each connected component of
![]() $M$
).
$M$
).
To equip readers with some feeling on the above decomposition which is not common in the literature, we now provide the coordinate expression of
![]() $\flat _{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D6FC})$
and
$\flat _{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D6FC})$
and
![]() $\unicode[STIX]{x1D6FC}_{X}$
in the Darboux chart
$\unicode[STIX]{x1D6FC}_{X}$
in the Darboux chart
![]() $(q_{1},\ldots ,q_{n},p_{1},\ldots ,p_{n},z)$
with respect to the canonical one-form
$(q_{1},\ldots ,q_{n},p_{1},\ldots ,p_{n},z)$
with respect to the canonical one-form
![]() $\unicode[STIX]{x1D706}_{0}=dz-\sum _{i=1}^{n}p_{i}\,dq_{i}$
on
$\unicode[STIX]{x1D706}_{0}=dz-\sum _{i=1}^{n}p_{i}\,dq_{i}$
on
![]() $\mathbb{R}^{2n+1}$
or more generally on the one-jet bundle
$\mathbb{R}^{2n+1}$
or more generally on the one-jet bundle
![]() $J^{1}(N)$
of a smooth
$J^{1}(N)$
of a smooth
![]() $n$
-manifold
$n$
-manifold
![]() $N$
. However, this coordinate expression will not be used in the rest of the present paper.
$N$
. However, this coordinate expression will not be used in the rest of the present paper.
We recall that for this contact form, the associated Reeb vector field is nothing but
We start with the expression of
![]() $\flat _{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D6FC})$
for a given one-form
$\flat _{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D6FC})$
for a given one-form
We denote
A direct computation using the defining equation of
![]() $\flat _{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D6FC})$
leads to
$\flat _{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D6FC})$
leads to
Proposition 2.4. Consider the standard contact structure
Then for the given one-form
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{0}\,dz+\sum _{i=1}^{n}a_{i}\,dq_{i}+\sum _{j=1}^{n}b_{j}\,dp_{j}$
,
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{0}\,dz+\sum _{i=1}^{n}a_{i}\,dq_{i}+\sum _{j=1}^{n}b_{j}\,dp_{j}$
,
Conversely, for the given
we obtain
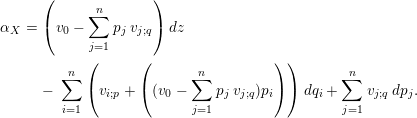 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FC}_{X} & = & \displaystyle \left(v_{0}-\mathop{\sum }_{j=1}^{n}p_{j}\,v_{j;q}\right)dz\nonumber\\ \displaystyle & & \displaystyle -\,\mathop{\sum }_{i=1}^{n}\left(v_{i;p}+\left((v_{0}-\mathop{\sum }_{j=1}^{n}p_{j}\,v_{j;q})p_{i}\right)\right)dq_{i}+\mathop{\sum }_{j=1}^{n}v_{j;q}\,dp_{j}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FC}_{X} & = & \displaystyle \left(v_{0}-\mathop{\sum }_{j=1}^{n}p_{j}\,v_{j;q}\right)dz\nonumber\\ \displaystyle & & \displaystyle -\,\mathop{\sum }_{i=1}^{n}\left(v_{i;p}+\left((v_{0}-\mathop{\sum }_{j=1}^{n}p_{j}\,v_{j;q})p_{i}\right)\right)dq_{i}+\mathop{\sum }_{j=1}^{n}v_{j;q}\,dp_{j}.\end{eqnarray}$$
Proof. Here we first recall the basic identity (2.4).
By definition,
![]() $\flat _{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D6FC})$
is determined by the equation
$\flat _{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D6FC})$
is determined by the equation
in the current case. A straightforward computation leads to the formula (2.5). Then (2.6) can be derived either by inverting this formula or by using the defining equation of
![]() $\unicode[STIX]{x1D6FC}_{X}$
, which is further reduced to
$\unicode[STIX]{x1D6FC}_{X}$
, which is further reduced to
We omit the details of the computation. ◻
Example 2.5. Again consider the canonical one-form
![]() $dz-\sum _{i=1}^{n}p_{i}\,dq_{i}$
. Then we obtain the following coordinate expression as a special case of (2.5)
$dz-\sum _{i=1}^{n}p_{i}\,dq_{i}$
. Then we obtain the following coordinate expression as a special case of (2.5)
2.2 Perturbation of contact forms of
 $(M,\unicode[STIX]{x1D709})$
$(M,\unicode[STIX]{x1D709})$
In this section, we exploit the discussion on the
![]() $\unicode[STIX]{x1D706}$
-dual vector fields and express the Reeb vector fields
$\unicode[STIX]{x1D706}$
-dual vector fields and express the Reeb vector fields
![]() $X_{f\unicode[STIX]{x1D706}}$
and the projection
$X_{f\unicode[STIX]{x1D706}}$
and the projection
![]() $\unicode[STIX]{x1D70B}_{f\unicode[STIX]{x1D706}}$
associated to the contact form
$\unicode[STIX]{x1D70B}_{f\unicode[STIX]{x1D706}}$
associated to the contact form
![]() $f\unicode[STIX]{x1D706}$
for a positive function
$f\unicode[STIX]{x1D706}$
for a positive function
![]() $f>0$
, in terms of those associated to the given contact form
$f>0$
, in terms of those associated to the given contact form
![]() $\unicode[STIX]{x1D706}$
and the
$\unicode[STIX]{x1D706}$
and the
![]() $\unicode[STIX]{x1D706}$
-dual vector fields of
$\unicode[STIX]{x1D706}$
-dual vector fields of
![]() $df$
.
$df$
.
Recalling Lemma 2.1, we can write
with
![]() $Y_{dg}\in \unicode[STIX]{x1D709}$
in a unique way for any smooth function
$Y_{dg}\in \unicode[STIX]{x1D709}$
in a unique way for any smooth function
![]() $g$
. Then by definition, we have
$g$
. Then by definition, we have
![]() $Y_{dg}=\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(\flat _{\unicode[STIX]{x1D706}}(dg))$
.
$Y_{dg}=\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(\flat _{\unicode[STIX]{x1D706}}(dg))$
.
We first compute the following useful explicit formula for the associated Reeb vector fields
![]() $X_{f\unicode[STIX]{x1D706}}$
in terms of
$X_{f\unicode[STIX]{x1D706}}$
in terms of
![]() $X_{\unicode[STIX]{x1D706}}$
and
$X_{\unicode[STIX]{x1D706}}$
and
![]() $Y_{dg}$
.
$Y_{dg}$
.
Proposition 2.6. (Perturbed Reeb vector field)
Denote
as above. Then we have
Proof. It turns out to be easier to consider
![]() $f\,X_{f\unicode[STIX]{x1D706}}$
which we compute below. First we have
$f\,X_{f\unicode[STIX]{x1D706}}$
which we compute below. First we have
with respect to the splitting
![]() $TM=\mathbb{R}\{X_{\unicode[STIX]{x1D706}}\}\oplus \unicode[STIX]{x1D709}$
for some constant
$TM=\mathbb{R}\{X_{\unicode[STIX]{x1D706}}\}\oplus \unicode[STIX]{x1D709}$
for some constant
![]() $c$
and
$c$
and
![]() $\unicode[STIX]{x1D702}\in \unicode[STIX]{x1D709}$
. We evaluate
$\unicode[STIX]{x1D702}\in \unicode[STIX]{x1D709}$
. We evaluate
It remains to derive the formula for
![]() $\unicode[STIX]{x1D702}$
. Using the formula
$\unicode[STIX]{x1D702}$
. Using the formula
and
![]() $\unicode[STIX]{x1D706}(\unicode[STIX]{x1D702})=0$
, we compute
$\unicode[STIX]{x1D706}(\unicode[STIX]{x1D702})=0$
, we compute
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D702}\!\rfloor d\unicode[STIX]{x1D706} & = & \displaystyle (fX_{f\unicode[STIX]{x1D706}})\!\rfloor d\unicode[STIX]{x1D706}\nonumber\\ \displaystyle & = & \displaystyle X_{f\unicode[STIX]{x1D706}}\!\rfloor d(f\unicode[STIX]{x1D706})-X_{f\unicode[STIX]{x1D706}}\!\rfloor (df\wedge \unicode[STIX]{x1D706})\nonumber\\ \displaystyle & = & \displaystyle -X_{f\unicode[STIX]{x1D706}}\!\rfloor (df\wedge \unicode[STIX]{x1D706})\nonumber\\ \displaystyle & = & \displaystyle -X_{f\unicode[STIX]{x1D706}}(f)\unicode[STIX]{x1D706}+\unicode[STIX]{x1D706}(X_{f\unicode[STIX]{x1D706}})\,df\nonumber\\ \displaystyle & = & \displaystyle -\frac{1}{f}(X_{\unicode[STIX]{x1D706}}+\unicode[STIX]{x1D702})(f)\unicode[STIX]{x1D706}+\frac{1}{f}\unicode[STIX]{x1D706}(X_{\unicode[STIX]{x1D706}}+\unicode[STIX]{x1D702})\,df\nonumber\\ \displaystyle & = & \displaystyle -\frac{1}{f}X_{\unicode[STIX]{x1D706}}(f)\unicode[STIX]{x1D706}-\frac{1}{f}\unicode[STIX]{x1D702}(f)\unicode[STIX]{x1D706}+\frac{1}{f}\,df.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D702}\!\rfloor d\unicode[STIX]{x1D706} & = & \displaystyle (fX_{f\unicode[STIX]{x1D706}})\!\rfloor d\unicode[STIX]{x1D706}\nonumber\\ \displaystyle & = & \displaystyle X_{f\unicode[STIX]{x1D706}}\!\rfloor d(f\unicode[STIX]{x1D706})-X_{f\unicode[STIX]{x1D706}}\!\rfloor (df\wedge \unicode[STIX]{x1D706})\nonumber\\ \displaystyle & = & \displaystyle -X_{f\unicode[STIX]{x1D706}}\!\rfloor (df\wedge \unicode[STIX]{x1D706})\nonumber\\ \displaystyle & = & \displaystyle -X_{f\unicode[STIX]{x1D706}}(f)\unicode[STIX]{x1D706}+\unicode[STIX]{x1D706}(X_{f\unicode[STIX]{x1D706}})\,df\nonumber\\ \displaystyle & = & \displaystyle -\frac{1}{f}(X_{\unicode[STIX]{x1D706}}+\unicode[STIX]{x1D702})(f)\unicode[STIX]{x1D706}+\frac{1}{f}\unicode[STIX]{x1D706}(X_{\unicode[STIX]{x1D706}}+\unicode[STIX]{x1D702})\,df\nonumber\\ \displaystyle & = & \displaystyle -\frac{1}{f}X_{\unicode[STIX]{x1D706}}(f)\unicode[STIX]{x1D706}-\frac{1}{f}\unicode[STIX]{x1D702}(f)\unicode[STIX]{x1D706}+\frac{1}{f}\,df.\nonumber\end{eqnarray}$$
Take value of
![]() $X_{\unicode[STIX]{x1D706}}$
for both sides, we get
$X_{\unicode[STIX]{x1D706}}$
for both sides, we get
![]() $\unicode[STIX]{x1D702}(f)=0$
, and hence
$\unicode[STIX]{x1D702}(f)=0$
, and hence
Setting
![]() $g=\log f$
, we can rewrite this into
$g=\log f$
, we can rewrite this into
In other words, we obtain
Therefore, by Lemma 2.1, we have obtained
![]() $\unicode[STIX]{x1D702}=Y_{dg}$
. Substituting this into (2.9) and dividing it by
$\unicode[STIX]{x1D702}=Y_{dg}$
. Substituting this into (2.9) and dividing it by
![]() $f$
, we have finished the proof.◻
$f$
, we have finished the proof.◻
Next we compare the contact projections
![]() $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}$
with
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}$
with
![]() $\unicode[STIX]{x1D70B}_{f\unicode[STIX]{x1D706}}$
associated to
$\unicode[STIX]{x1D70B}_{f\unicode[STIX]{x1D706}}$
associated to
![]() $\unicode[STIX]{x1D706}$
and
$\unicode[STIX]{x1D706}$
and
![]() $f\unicode[STIX]{x1D706}$
, respectively.
$f\unicode[STIX]{x1D706}$
, respectively.
Proposition 2.7. (Perturbed contact projection)
Let
![]() $(M,\unicode[STIX]{x1D709})$
be a contact manifold and let
$(M,\unicode[STIX]{x1D709})$
be a contact manifold and let
![]() $\unicode[STIX]{x1D706}$
be a contact form that is,
$\unicode[STIX]{x1D706}$
be a contact form that is,
![]() $\ker \unicode[STIX]{x1D706}=\unicode[STIX]{x1D709}$
. Let
$\ker \unicode[STIX]{x1D706}=\unicode[STIX]{x1D709}$
. Let
![]() $f$
be a positive smooth function and
$f$
be a positive smooth function and
![]() $f\,\unicode[STIX]{x1D706}$
be its associated contact form. Denote by
$f\,\unicode[STIX]{x1D706}$
be its associated contact form. Denote by
![]() $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}$
and
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}$
and
![]() $\unicode[STIX]{x1D70B}_{f\,\unicode[STIX]{x1D706}}$
be their associated
$\unicode[STIX]{x1D70B}_{f\,\unicode[STIX]{x1D706}}$
be their associated
![]() $\unicode[STIX]{x1D709}$
-projection. Then
$\unicode[STIX]{x1D709}$
-projection. Then
for the function
![]() $g=\log f$
.
$g=\log f$
.
Proof. We compute
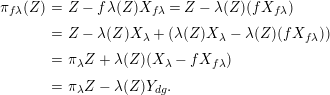 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}_{f\unicode[STIX]{x1D706}}(Z) & = & \displaystyle Z-f\unicode[STIX]{x1D706}(Z)X_{f\unicode[STIX]{x1D706}}=Z-\unicode[STIX]{x1D706}(Z)(fX_{f\unicode[STIX]{x1D706}})\nonumber\\ \displaystyle & = & \displaystyle Z-\unicode[STIX]{x1D706}(Z)X_{\unicode[STIX]{x1D706}}+(\unicode[STIX]{x1D706}(Z)X_{\unicode[STIX]{x1D706}}-\unicode[STIX]{x1D706}(Z)(fX_{f\unicode[STIX]{x1D706}}))\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}Z+\unicode[STIX]{x1D706}(Z)(X_{\unicode[STIX]{x1D706}}-fX_{f\unicode[STIX]{x1D706}})\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}Z-\unicode[STIX]{x1D706}(Z)Y_{dg}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}_{f\unicode[STIX]{x1D706}}(Z) & = & \displaystyle Z-f\unicode[STIX]{x1D706}(Z)X_{f\unicode[STIX]{x1D706}}=Z-\unicode[STIX]{x1D706}(Z)(fX_{f\unicode[STIX]{x1D706}})\nonumber\\ \displaystyle & = & \displaystyle Z-\unicode[STIX]{x1D706}(Z)X_{\unicode[STIX]{x1D706}}+(\unicode[STIX]{x1D706}(Z)X_{\unicode[STIX]{x1D706}}-\unicode[STIX]{x1D706}(Z)(fX_{f\unicode[STIX]{x1D706}}))\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}Z+\unicode[STIX]{x1D706}(Z)(X_{\unicode[STIX]{x1D706}}-fX_{f\unicode[STIX]{x1D706}})\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}Z-\unicode[STIX]{x1D706}(Z)Y_{dg}.\nonumber\end{eqnarray}$$
This finishes the proof. ◻
2.3 Linearization formula for the perturbed contact form
We next study the relationship between the linearization of
![]() $\unicode[STIX]{x1D6F6}_{\unicode[STIX]{x1D706}}(z)={\dot{z}}-TX_{f\unicode[STIX]{x1D706}}(z)$
which we denote by
$\unicode[STIX]{x1D6F6}_{\unicode[STIX]{x1D706}}(z)={\dot{z}}-TX_{f\unicode[STIX]{x1D706}}(z)$
which we denote by
with respect to the triad connection of
![]() $(M,\unicode[STIX]{x1D706},J)$
(see [Reference Oh and WangOW2, Proposition 7.6]) for a given function
$(M,\unicode[STIX]{x1D706},J)$
(see [Reference Oh and WangOW2, Proposition 7.6]) for a given function
![]() $f$
. Substituting
$f$
. Substituting
into this formula, we derive
Lemma 2.8. (Linearization)
Let
![]() $\unicode[STIX]{x1D6FB}$
be the triad connection of
$\unicode[STIX]{x1D6FB}$
be the triad connection of
![]() $(M,f\unicode[STIX]{x1D706},J)$
. Then for any vector field
$(M,f\unicode[STIX]{x1D706},J)$
. Then for any vector field
![]() $Z$
along a Reeb orbit
$Z$
along a Reeb orbit
![]() $z=(\unicode[STIX]{x1D6FE}(T\cdot ),o_{\unicode[STIX]{x1D6FE}(T\cdot )})$
,
$z=(\unicode[STIX]{x1D6FE}(T\cdot ),o_{\unicode[STIX]{x1D6FE}(T\cdot )})$
,
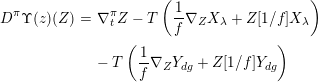 $$\begin{eqnarray}\displaystyle D^{\unicode[STIX]{x1D70B}}\unicode[STIX]{x1D6F6}(z)(Z) & = & \displaystyle \unicode[STIX]{x1D6FB}_{t}^{\unicode[STIX]{x1D70B}}Z-T\left(\frac{1}{f}\unicode[STIX]{x1D6FB}_{Z}X_{\unicode[STIX]{x1D706}}+Z[1/f]X_{\unicode[STIX]{x1D706}}\right)\nonumber\\ \displaystyle & & \displaystyle -\,T\left(\frac{1}{f}\unicode[STIX]{x1D6FB}_{Z}Y_{dg}+Z[1/f]Y_{dg}\right)\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle D^{\unicode[STIX]{x1D70B}}\unicode[STIX]{x1D6F6}(z)(Z) & = & \displaystyle \unicode[STIX]{x1D6FB}_{t}^{\unicode[STIX]{x1D70B}}Z-T\left(\frac{1}{f}\unicode[STIX]{x1D6FB}_{Z}X_{\unicode[STIX]{x1D706}}+Z[1/f]X_{\unicode[STIX]{x1D706}}\right)\nonumber\\ \displaystyle & & \displaystyle -\,T\left(\frac{1}{f}\unicode[STIX]{x1D6FB}_{Z}Y_{dg}+Z[1/f]Y_{dg}\right)\end{eqnarray}$$
Proof. Let
![]() $\unicode[STIX]{x1D6FB}$
be the triad connection of
$\unicode[STIX]{x1D6FB}$
be the triad connection of
![]() $(M,f\unicode[STIX]{x1D706},J)$
. Then by definition its torsion
$(M,f\unicode[STIX]{x1D706},J)$
. Then by definition its torsion
![]() $T$
satisfies the axiom
$T$
satisfies the axiom
![]() $T(X_{\unicode[STIX]{x1D706}},Z)=0$
for any vector field
$T(X_{\unicode[STIX]{x1D706}},Z)=0$
for any vector field
![]() $Z$
on
$Z$
on
![]() $M$
(see [Reference Oh and WangOW1, Theorem 1]). Using this property, as in [Reference Oh and WangOW2, Section 7], we compute
$M$
(see [Reference Oh and WangOW1, Theorem 1]). Using this property, as in [Reference Oh and WangOW2, Section 7], we compute
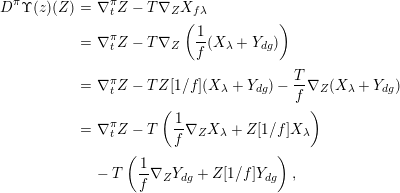 $$\begin{eqnarray}\displaystyle D^{\unicode[STIX]{x1D70B}}\unicode[STIX]{x1D6F6}(z)(Z) & = & \displaystyle \unicode[STIX]{x1D6FB}_{t}^{\unicode[STIX]{x1D70B}}Z-T\unicode[STIX]{x1D6FB}_{Z}X_{f\unicode[STIX]{x1D706}}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FB}_{t}^{\unicode[STIX]{x1D70B}}Z-T\unicode[STIX]{x1D6FB}_{Z}\left(\frac{1}{f}(X_{\unicode[STIX]{x1D706}}+Y_{dg})\right)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FB}_{t}^{\unicode[STIX]{x1D70B}}Z-TZ[1/f](X_{\unicode[STIX]{x1D706}}+Y_{dg})-\frac{T}{f}\unicode[STIX]{x1D6FB}_{Z}(X_{\unicode[STIX]{x1D706}}+Y_{dg})\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FB}_{t}^{\unicode[STIX]{x1D70B}}Z-T\left(\frac{1}{f}\unicode[STIX]{x1D6FB}_{Z}X_{\unicode[STIX]{x1D706}}+Z[1/f]X_{\unicode[STIX]{x1D706}}\right)\nonumber\\ \displaystyle & & \displaystyle -\,T\left(\frac{1}{f}\unicode[STIX]{x1D6FB}_{Z}Y_{dg}+Z[1/f]Y_{dg}\right),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle D^{\unicode[STIX]{x1D70B}}\unicode[STIX]{x1D6F6}(z)(Z) & = & \displaystyle \unicode[STIX]{x1D6FB}_{t}^{\unicode[STIX]{x1D70B}}Z-T\unicode[STIX]{x1D6FB}_{Z}X_{f\unicode[STIX]{x1D706}}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FB}_{t}^{\unicode[STIX]{x1D70B}}Z-T\unicode[STIX]{x1D6FB}_{Z}\left(\frac{1}{f}(X_{\unicode[STIX]{x1D706}}+Y_{dg})\right)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FB}_{t}^{\unicode[STIX]{x1D70B}}Z-TZ[1/f](X_{\unicode[STIX]{x1D706}}+Y_{dg})-\frac{T}{f}\unicode[STIX]{x1D6FB}_{Z}(X_{\unicode[STIX]{x1D706}}+Y_{dg})\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FB}_{t}^{\unicode[STIX]{x1D70B}}Z-T\left(\frac{1}{f}\unicode[STIX]{x1D6FB}_{Z}X_{\unicode[STIX]{x1D706}}+Z[1/f]X_{\unicode[STIX]{x1D706}}\right)\nonumber\\ \displaystyle & & \displaystyle -\,T\left(\frac{1}{f}\unicode[STIX]{x1D6FB}_{Z}Y_{dg}+Z[1/f]Y_{dg}\right),\nonumber\end{eqnarray}$$
which finishes the proof. ◻
We note that when
![]() $f\equiv 1$
, the above formula reduces to the standard formula
$f\equiv 1$
, the above formula reduces to the standard formula
which is further reduced to
for any contact triad
![]() $(M,\unicode[STIX]{x1D706},J)$
. (See [Reference Oh and WangOW2, Section 7] for some discussion on this formula.)
$(M,\unicode[STIX]{x1D706},J)$
. (See [Reference Oh and WangOW2, Section 7] for some discussion on this formula.)
3 The locus foliated by closed Reeb orbits
3.1 Definition of Morse–Bott contact form
Let
![]() $(M,\unicode[STIX]{x1D709})$
be a contact manifold and
$(M,\unicode[STIX]{x1D709})$
be a contact manifold and
![]() $\unicode[STIX]{x1D706}$
be a contact form of
$\unicode[STIX]{x1D706}$
be a contact form of
![]() $\unicode[STIX]{x1D709}$
. We would like to study the linearization of the equation
$\unicode[STIX]{x1D709}$
. We would like to study the linearization of the equation
![]() ${\dot{x}}=X_{\unicode[STIX]{x1D706}}(x)$
along a closed Reeb orbit. Let
${\dot{x}}=X_{\unicode[STIX]{x1D706}}(x)$
along a closed Reeb orbit. Let
![]() $\unicode[STIX]{x1D6FE}$
be a closed Reeb orbit of period
$\unicode[STIX]{x1D6FE}$
be a closed Reeb orbit of period
![]() $T>0$
. In other words,
$T>0$
. In other words,
![]() $\unicode[STIX]{x1D6FE}:\mathbb{R}\rightarrow M$
is a solution of
$\unicode[STIX]{x1D6FE}:\mathbb{R}\rightarrow M$
is a solution of
![]() $\dot{\unicode[STIX]{x1D6FE}}=X_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D6FE})$
satisfying
$\dot{\unicode[STIX]{x1D6FE}}=X_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D6FE})$
satisfying
![]() $\unicode[STIX]{x1D6FE}(t+T)=\unicode[STIX]{x1D6FE}(t)$
.
$\unicode[STIX]{x1D6FE}(t+T)=\unicode[STIX]{x1D6FE}(t)$
.
By definition, we can write
![]() $\unicode[STIX]{x1D6FE}(t)=\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D706}}}^{t}(\unicode[STIX]{x1D6FE}(0))$
for the Reeb flow
$\unicode[STIX]{x1D6FE}(t)=\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D706}}}^{t}(\unicode[STIX]{x1D6FE}(0))$
for the Reeb flow
![]() $\unicode[STIX]{x1D719}^{t}=\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D706}}}^{t}$
of the Reeb vector field
$\unicode[STIX]{x1D719}^{t}=\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D706}}}^{t}$
of the Reeb vector field
![]() $X_{\unicode[STIX]{x1D706}}$
. In particular
$X_{\unicode[STIX]{x1D706}}$
. In particular
![]() $p=\unicode[STIX]{x1D6FE}(0)$
is a fixed point of the diffeomorphism
$p=\unicode[STIX]{x1D6FE}(0)$
is a fixed point of the diffeomorphism
![]() $\unicode[STIX]{x1D719}^{T}$
when
$\unicode[STIX]{x1D719}^{T}$
when
![]() $\unicode[STIX]{x1D6FE}$
is a closed Reeb orbit of period
$\unicode[STIX]{x1D6FE}$
is a closed Reeb orbit of period
![]() $T$
. Since
$T$
. Since
![]() ${\mathcal{L}}_{X_{\unicode[STIX]{x1D706}}}\unicode[STIX]{x1D706}=0$
, the contact diffeomorphism
${\mathcal{L}}_{X_{\unicode[STIX]{x1D706}}}\unicode[STIX]{x1D706}=0$
, the contact diffeomorphism
![]() $\unicode[STIX]{x1D719}^{T}$
canonically induces the isomorphism
$\unicode[STIX]{x1D719}^{T}$
canonically induces the isomorphism
which is the linearized Poincaré return map
![]() $\unicode[STIX]{x1D719}^{T}$
restricted to
$\unicode[STIX]{x1D719}^{T}$
restricted to
![]() $\unicode[STIX]{x1D709}_{p}$
via the splitting
$\unicode[STIX]{x1D709}_{p}$
via the splitting
Definition 3.1. Let
![]() $\unicode[STIX]{x1D6FE}$
be a closed Reeb orbit with period
$\unicode[STIX]{x1D6FE}$
be a closed Reeb orbit with period
![]() $T>0$
and denote by
$T>0$
and denote by
![]() $z:S^{1}\rightarrow M$
the map defined by
$z:S^{1}\rightarrow M$
the map defined by
![]() $z(t)=\unicode[STIX]{x1D6FE}(Tt)$
. We say a
$z(t)=\unicode[STIX]{x1D6FE}(Tt)$
. We say a
![]() $T$
-closed Reeb orbit
$T$
-closed Reeb orbit
![]() $(T,z)$
is nondegenerate if the linearized return map
$(T,z)$
is nondegenerate if the linearized return map
![]() $\unicode[STIX]{x1D6F9}_{z;p}:\unicode[STIX]{x1D709}_{p}\rightarrow \unicode[STIX]{x1D709}_{p}$
with
$\unicode[STIX]{x1D6F9}_{z;p}:\unicode[STIX]{x1D709}_{p}\rightarrow \unicode[STIX]{x1D709}_{p}$
with
![]() $p=\unicode[STIX]{x1D6FE}(0)$
has no eigenvalue 1.
$p=\unicode[STIX]{x1D6FE}(0)$
has no eigenvalue 1.
Denote
![]() $\operatorname{Cont}(M,\unicode[STIX]{x1D709})$
the set of contact one-forms with respect to the contact structure
$\operatorname{Cont}(M,\unicode[STIX]{x1D709})$
the set of contact one-forms with respect to the contact structure
![]() $\unicode[STIX]{x1D709}$
and
$\unicode[STIX]{x1D709}$
and
![]() ${\mathcal{L}}(M)=C^{\infty }(S^{1},M)$
the space of loops
${\mathcal{L}}(M)=C^{\infty }(S^{1},M)$
the space of loops
![]() $z:S^{1}=\mathbb{R}/\mathbb{Z}\rightarrow M$
. We would like to consider the bundle
$z:S^{1}=\mathbb{R}/\mathbb{Z}\rightarrow M$
. We would like to consider the bundle
![]() ${\mathcal{L}}$
over the product
${\mathcal{L}}$
over the product
![]() $(0,\infty )\times {\mathcal{L}}(M)\times \operatorname{Cont}(M,\unicode[STIX]{x1D709})$
whose fiber at
$(0,\infty )\times {\mathcal{L}}(M)\times \operatorname{Cont}(M,\unicode[STIX]{x1D709})$
whose fiber at
![]() $(T,z,\unicode[STIX]{x1D706})$
is given by the space
$(T,z,\unicode[STIX]{x1D706})$
is given by the space
![]() $C^{\infty }(z^{\ast }TM)$
of sections of the bundle
$C^{\infty }(z^{\ast }TM)$
of sections of the bundle
![]() $z^{\ast }TM\rightarrow S^{1}$
. We consider the assignment
$z^{\ast }TM\rightarrow S^{1}$
. We consider the assignment
which is a section. Then
![]() $(T,z,\unicode[STIX]{x1D706})\in \unicode[STIX]{x1D6F6}^{-1}(0):=\mathfrak{Reeb}(M,\unicode[STIX]{x1D709})$
if and only if there exists some closed Reeb orbit
$(T,z,\unicode[STIX]{x1D706})\in \unicode[STIX]{x1D6F6}^{-1}(0):=\mathfrak{Reeb}(M,\unicode[STIX]{x1D709})$
if and only if there exists some closed Reeb orbit
![]() $\unicode[STIX]{x1D6FE}:\mathbb{R}\rightarrow M$
with period
$\unicode[STIX]{x1D6FE}:\mathbb{R}\rightarrow M$
with period
![]() $T$
, such that
$T$
, such that
![]() $z(\cdot )=\unicode[STIX]{x1D6FE}(T\cdot )$
.
$z(\cdot )=\unicode[STIX]{x1D6FE}(T\cdot )$
.
We first start with the standard notion, applied to the set of closed Reeb orbits, of Morse–Bott critical manifolds introduced by Bott in [Reference BottBot]:
Definition 3.2. We call a contact form
![]() $\unicode[STIX]{x1D706}$
standard Morse–Bott type if every connected component of
$\unicode[STIX]{x1D706}$
standard Morse–Bott type if every connected component of
![]() $\mathfrak{Reeb}(M,\unicode[STIX]{x1D706})$
is a smooth submanifold of
$\mathfrak{Reeb}(M,\unicode[STIX]{x1D706})$
is a smooth submanifold of
![]() $(0,\infty )\times {\mathcal{L}}(M)$
with its tangent space at every pair
$(0,\infty )\times {\mathcal{L}}(M)$
with its tangent space at every pair
![]() $(T,z)\in \mathfrak{Reeb}(M,\unicode[STIX]{x1D706})$
therein coincides with
$(T,z)\in \mathfrak{Reeb}(M,\unicode[STIX]{x1D706})$
therein coincides with
![]() $\ker d_{(T,z)}\unicode[STIX]{x1D6F6}$
.
$\ker d_{(T,z)}\unicode[STIX]{x1D6F6}$
.
The following is an immediate consequence of this definition.
Lemma 3.3. Suppose
![]() $\unicode[STIX]{x1D706}$
is of standard Morse–Bott type, then on each connected component of
$\unicode[STIX]{x1D706}$
is of standard Morse–Bott type, then on each connected component of
![]() $\mathfrak{Reeb}(M,\unicode[STIX]{x1D706})$
, the period remains constant.
$\mathfrak{Reeb}(M,\unicode[STIX]{x1D706})$
, the period remains constant.
Proof. Let
![]() $(T_{0},z_{0})$
and
$(T_{0},z_{0})$
and
![]() $(T_{1},z_{1})$
be two elements in the same connected component of
$(T_{1},z_{1})$
be two elements in the same connected component of
![]() $\mathfrak{Reeb}(M,\unicode[STIX]{x1D706})$
. We connect them by a smooth one-parameter family
$\mathfrak{Reeb}(M,\unicode[STIX]{x1D706})$
. We connect them by a smooth one-parameter family
![]() $(T_{s},z_{s})$
for
$(T_{s},z_{s})$
for
![]() $0\leqslant s\leqslant 1$
. Since
$0\leqslant s\leqslant 1$
. Since
![]() $\dot{z_{s}}=T_{s}X_{\unicode[STIX]{x1D706}}(z_{s})$
and then
$\dot{z_{s}}=T_{s}X_{\unicode[STIX]{x1D706}}(z_{s})$
and then
![]() $T_{s}=\int _{S^{1}}z_{s}^{\ast }\unicode[STIX]{x1D706}$
, it is enough to prove
$T_{s}=\int _{S^{1}}z_{s}^{\ast }\unicode[STIX]{x1D706}$
, it is enough to prove
We compute
 $$\begin{eqnarray}\displaystyle \frac{d}{ds}z_{s}^{\ast }\unicode[STIX]{x1D706} & = & \displaystyle z_{s}^{\ast }(d(z_{s}^{\prime }\!\rfloor \unicode[STIX]{x1D706})+z_{s}^{\prime }\!\rfloor d\unicode[STIX]{x1D706})\nonumber\\ \displaystyle & = & \displaystyle d(z_{s}^{\ast }(z_{s}^{\prime }\!\rfloor \unicode[STIX]{x1D706}))+z_{s}^{\ast }(z_{s}^{\prime }\!\rfloor d\unicode[STIX]{x1D706})\nonumber\\ \displaystyle & = & \displaystyle d(z_{s}^{\ast }(z_{s}^{\prime }\!\rfloor \unicode[STIX]{x1D706})).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{d}{ds}z_{s}^{\ast }\unicode[STIX]{x1D706} & = & \displaystyle z_{s}^{\ast }(d(z_{s}^{\prime }\!\rfloor \unicode[STIX]{x1D706})+z_{s}^{\prime }\!\rfloor d\unicode[STIX]{x1D706})\nonumber\\ \displaystyle & = & \displaystyle d(z_{s}^{\ast }(z_{s}^{\prime }\!\rfloor \unicode[STIX]{x1D706}))+z_{s}^{\ast }(z_{s}^{\prime }\!\rfloor d\unicode[STIX]{x1D706})\nonumber\\ \displaystyle & = & \displaystyle d(z_{s}^{\ast }(z_{s}^{\prime }\!\rfloor \unicode[STIX]{x1D706})).\nonumber\end{eqnarray}$$
Here we use
![]() $z_{s}^{\prime }$
to denote the derivative with respect to
$z_{s}^{\prime }$
to denote the derivative with respect to
![]() $s$
. The last equality comes from the fact that
$s$
. The last equality comes from the fact that
![]() $\dot{z_{s}}$
is parallel to
$\dot{z_{s}}$
is parallel to
![]() $X_{\unicode[STIX]{x1D706}}$
. Therefore, we obtain by Stokes formula that
$X_{\unicode[STIX]{x1D706}}$
. Therefore, we obtain by Stokes formula that
and finish the proof. ◻
Now we prove
Lemma 3.4. Let
![]() $\unicode[STIX]{x1D706}$
be standard Morse–Bott type. Fix a connected component
$\unicode[STIX]{x1D706}$
be standard Morse–Bott type. Fix a connected component
![]() ${\mathcal{R}}\subset \mathfrak{Reeb}(M,\unicode[STIX]{x1D706})$
and denote by
${\mathcal{R}}\subset \mathfrak{Reeb}(M,\unicode[STIX]{x1D706})$
and denote by
![]() $Q\subset M$
the locus of the corresponding closed Reeb orbits. Then
$Q\subset M$
the locus of the corresponding closed Reeb orbits. Then
![]() $Q$
is a smooth immersed submanifold which carries a natural locally free
$Q$
is a smooth immersed submanifold which carries a natural locally free
![]() $S^{1}$
-action induced by the Reeb flow over one period.
$S^{1}$
-action induced by the Reeb flow over one period.
Proof. Consider the evaluation map
![]() $ev_{{\mathcal{R}}}:\mathfrak{Reeb}(M,\unicode[STIX]{x1D706})\rightarrow M$
defined by
$ev_{{\mathcal{R}}}:\mathfrak{Reeb}(M,\unicode[STIX]{x1D706})\rightarrow M$
defined by
![]() $ev_{{\mathcal{R}}}(T,z)=z(0)$
. It is easy to prove that the map is a local immersion and so
$ev_{{\mathcal{R}}}(T,z)=z(0)$
. It is easy to prove that the map is a local immersion and so
![]() $Q$
is an immersed submanifold. Since the closed Reeb orbits have constant period
$Q$
is an immersed submanifold. Since the closed Reeb orbits have constant period
![]() $T>0$
by Lemma 3.3, the action is obviously locally free and so
$T>0$
by Lemma 3.3, the action is obviously locally free and so
![]() $ev_{{\mathcal{R}}}$
is an immersion and so
$ev_{{\mathcal{R}}}$
is an immersion and so
![]() $Q$
is immersed in
$Q$
is immersed in
![]() $M$
. This finishes the proof.◻
$M$
. This finishes the proof.◻
However,
![]() $Q$
may not be embedded in general along the locus of multiple orbits.
$Q$
may not be embedded in general along the locus of multiple orbits.
Partially following [Reference BourgeoisBou], from now on in the rest of the paper, we always assume
![]() $Q$
is embedded and compact. Denote
$Q$
is embedded and compact. Denote
![]() $\unicode[STIX]{x1D714}_{Q}:=i_{Q}^{\ast }d\unicode[STIX]{x1D706}$
and
$\unicode[STIX]{x1D714}_{Q}:=i_{Q}^{\ast }d\unicode[STIX]{x1D706}$
and
We warn readers that the Morse–Bott condition does not imply that the form
![]() $\unicode[STIX]{x1D714}_{Q}$
has constant rank, and hence the dimension of this kernel may vary pointwise on
$\unicode[STIX]{x1D714}_{Q}$
has constant rank, and hence the dimension of this kernel may vary pointwise on
![]() $Q$
. However, if it does,
$Q$
. However, if it does,
![]() $\ker \unicode[STIX]{x1D714}_{Q}$
defines an integrable distribution and so defines a foliation, denoted by
$\ker \unicode[STIX]{x1D714}_{Q}$
defines an integrable distribution and so defines a foliation, denoted by
![]() ${\mathcal{F}}$
, on
${\mathcal{F}}$
, on
![]() $Q$
. Since
$Q$
. Since
![]() $Q$
is also foliated by closed Reeb orbits and
$Q$
is also foliated by closed Reeb orbits and
![]() ${\mathcal{L}}_{X_{\unicode[STIX]{x1D706}}}d\unicode[STIX]{x1D706}=0$
, it follows that
${\mathcal{L}}_{X_{\unicode[STIX]{x1D706}}}d\unicode[STIX]{x1D706}=0$
, it follows that
![]() ${\mathcal{L}}_{X_{\unicode[STIX]{x1D706}}}\unicode[STIX]{x1D714}_{Q}=0$
when we restrict everything on
${\mathcal{L}}_{X_{\unicode[STIX]{x1D706}}}\unicode[STIX]{x1D714}_{Q}=0$
when we restrict everything on
![]() $Q$
. Therefore, each leaf of the foliation consists of closed Reeb orbits. Motivated by this, we also impose the condition that the two-form
$Q$
. Therefore, each leaf of the foliation consists of closed Reeb orbits. Motivated by this, we also impose the condition that the two-form
![]() $\unicode[STIX]{x1D714}_{Q}$
has constant rank.
$\unicode[STIX]{x1D714}_{Q}$
has constant rank.
Definition 3.5. (Compare with Definition 1.7 [Reference BourgeoisBou])
We say that the contact form
![]() $\unicode[STIX]{x1D706}$
is of Morse–Bott type if it satisfies the following:
$\unicode[STIX]{x1D706}$
is of Morse–Bott type if it satisfies the following:
(1) every connected component of
 $\mathfrak{Reeb}(M,\unicode[STIX]{x1D706})$
is a smooth submanifold of
$\mathfrak{Reeb}(M,\unicode[STIX]{x1D706})$
is a smooth submanifold of
 $(0,\infty )\times {\mathcal{L}}(M)$
with its tangent space at every pair
$(0,\infty )\times {\mathcal{L}}(M)$
with its tangent space at every pair
 $(T,z)\in \mathfrak{Reeb}(M,\unicode[STIX]{x1D706})$
therein coincides with
$(T,z)\in \mathfrak{Reeb}(M,\unicode[STIX]{x1D706})$
therein coincides with
 $\ker d_{(T,z)}\unicode[STIX]{x1D6F6}$
;
$\ker d_{(T,z)}\unicode[STIX]{x1D6F6}$
;(2)
 $Q$
is embedded;
$Q$
is embedded;(3)
 $\unicode[STIX]{x1D714}_{Q}$
has constant rank on
$\unicode[STIX]{x1D714}_{Q}$
has constant rank on
 $Q$
.
$Q$
.
3.2 Structure of the locus of closed Reeb orbits
Let
![]() $\unicode[STIX]{x1D706}$
be a Morse–Bott contact form of
$\unicode[STIX]{x1D706}$
be a Morse–Bott contact form of
![]() $(M,\unicode[STIX]{x1D709})$
and
$(M,\unicode[STIX]{x1D709})$
and
![]() $X_{\unicode[STIX]{x1D706}}$
its Reeb vector field. Let
$X_{\unicode[STIX]{x1D706}}$
its Reeb vector field. Let
![]() $Q$
be as in Definition 3.5. In general,
$Q$
be as in Definition 3.5. In general,
![]() $Q$
carries a natural locally free
$Q$
carries a natural locally free
![]() $S^{1}$
-action induced by the Reeb flow
$S^{1}$
-action induced by the Reeb flow
![]() $\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D706}}}^{T}$
(see Lemma 3.4). Then by the general theory of compact Lie group actions (see [Reference HelgasonHe] for example), the action has a finite number of orbit types which have their minimal periods,
$\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D706}}}^{T}$
(see Lemma 3.4). Then by the general theory of compact Lie group actions (see [Reference HelgasonHe] for example), the action has a finite number of orbit types which have their minimal periods,
![]() $T/m$
for some integer
$T/m$
for some integer
![]() $m\geqslant 1$
. The set of orbit spaces
$m\geqslant 1$
. The set of orbit spaces
![]() $Q/S^{1}$
carries natural orbifold structure at each multiple orbit with its isotropy group
$Q/S^{1}$
carries natural orbifold structure at each multiple orbit with its isotropy group
![]() $\mathbb{Z}/m$
for some
$\mathbb{Z}/m$
for some
![]() $m$
.
$m$
.
Remark 3.6. Here we would like to mention that the
![]() $S^{1}$
-action induced by
$S^{1}$
-action induced by
![]() $\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D706}}}^{T}$
on
$\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D706}}}^{T}$
on
![]() $Q$
may not be effective: it is possible that the connected component
$Q$
may not be effective: it is possible that the connected component
![]() $\mathfrak{R}$
of
$\mathfrak{R}$
of
![]() $\mathfrak{Reeb}(M,\unicode[STIX]{x1D706})$
can consist entirely of multiple orbits.
$\mathfrak{Reeb}(M,\unicode[STIX]{x1D706})$
can consist entirely of multiple orbits.
Now we fix a connected component of
![]() $Q$
and just denote it by
$Q$
and just denote it by
![]() $Q$
itself. Denote
$Q$
itself. Denote
![]() $\unicode[STIX]{x1D703}=i_{Q}^{\ast }\unicode[STIX]{x1D706}$
. We note that the two-form
$\unicode[STIX]{x1D703}=i_{Q}^{\ast }\unicode[STIX]{x1D706}$
. We note that the two-form
![]() $\unicode[STIX]{x1D714}_{Q}=d\unicode[STIX]{x1D703}$
is assumed to have constant rank on
$\unicode[STIX]{x1D714}_{Q}=d\unicode[STIX]{x1D703}$
is assumed to have constant rank on
![]() $Q$
by the definition of Morse–Bott contact form in Definition 3.5.
$Q$
by the definition of Morse–Bott contact form in Definition 3.5.
The following is an immediate consequence of the definition but exhibits a particularity of the null foliation of the presymplectic manifold
![]() $(Q,\unicode[STIX]{x1D714}_{Q})$
arising from the locus of closed Reeb orbits. We note that
$(Q,\unicode[STIX]{x1D714}_{Q})$
arising from the locus of closed Reeb orbits. We note that
![]() $\ker \unicode[STIX]{x1D714}_{Q}$
carries a natural splitting
$\ker \unicode[STIX]{x1D714}_{Q}$
carries a natural splitting
Lemma 3.7. The distribution
![]() $(\ker \unicode[STIX]{x1D714}_{Q})\cap \unicode[STIX]{x1D709}|_{Q}$
on
$(\ker \unicode[STIX]{x1D714}_{Q})\cap \unicode[STIX]{x1D709}|_{Q}$
on
![]() $Q$
is integrable.
$Q$
is integrable.
Proof. Let
![]() $X$
,
$X$
,
![]() $Y$
be vector fields on
$Y$
be vector fields on
![]() $Q$
such that
$Q$
such that
![]() $X$
,
$X$
,
![]() $Y\in (\ker \unicode[STIX]{x1D714}_{Q})\cap \unicode[STIX]{x1D709}|_{Q}$
. Then
$Y\in (\ker \unicode[STIX]{x1D714}_{Q})\cap \unicode[STIX]{x1D709}|_{Q}$
. Then
![]() $[X,Y]\in \ker \unicode[STIX]{x1D714}_{Q}$
since
$[X,Y]\in \ker \unicode[STIX]{x1D714}_{Q}$
since
![]() $\unicode[STIX]{x1D714}_{Q}$
is a closed two-form whose null distribution is integrable. At the same time, we compute
$\unicode[STIX]{x1D714}_{Q}$
is a closed two-form whose null distribution is integrable. At the same time, we compute
![]() $i_{Q}^{\ast }\unicode[STIX]{x1D706}([X,Y])=X[\unicode[STIX]{x1D706}(Y)]-Y[\unicode[STIX]{x1D706}(X)]-\unicode[STIX]{x1D714}_{Q}(X,Y)=0$
where the first two terms vanish since
$i_{Q}^{\ast }\unicode[STIX]{x1D706}([X,Y])=X[\unicode[STIX]{x1D706}(Y)]-Y[\unicode[STIX]{x1D706}(X)]-\unicode[STIX]{x1D714}_{Q}(X,Y)=0$
where the first two terms vanish since
![]() $X$
,
$X$
,
![]() $Y\in \unicode[STIX]{x1D709}$
and the third vanishes because
$Y\in \unicode[STIX]{x1D709}$
and the third vanishes because
![]() $X\in \ker \unicode[STIX]{x1D714}_{Q}$
. This proves
$X\in \ker \unicode[STIX]{x1D714}_{Q}$
. This proves
![]() $[X,Y]\in \ker \unicode[STIX]{x1D714}_{Q}\cap \unicode[STIX]{x1D709}|_{Q}$
, which finishes the proof.◻
$[X,Y]\in \ker \unicode[STIX]{x1D714}_{Q}\cap \unicode[STIX]{x1D709}|_{Q}$
, which finishes the proof.◻
Therefore,
![]() $\ker \unicode[STIX]{x1D714}_{Q}\cap \unicode[STIX]{x1D709}|_{Q}$
defines another foliation
$\ker \unicode[STIX]{x1D714}_{Q}\cap \unicode[STIX]{x1D709}|_{Q}$
defines another foliation
![]() ${\mathcal{N}}$
on
${\mathcal{N}}$
on
![]() $Q$
, and hence
$Q$
, and hence
Note that this splitting is
![]() $S^{1}$
-invariant.
$S^{1}$
-invariant.
We now recall some basic properties of presymplectic manifold [Reference GotayG] and its canonical neighborhood theorem. Fix an
![]() $S^{1}$
-equivariant splitting of
$S^{1}$
-equivariant splitting of
![]() $TQ$
$TQ$
by choosing an
![]() $S^{1}$
-invariant complementary subbundle
$S^{1}$
-invariant complementary subbundle
![]() $G\subset TQ$
. This splitting is not unique but its choice will not matter for the coming discussions. The null foliation carries a natural transverse symplectic form in general [Reference GotayG]. Since the distribution
$G\subset TQ$
. This splitting is not unique but its choice will not matter for the coming discussions. The null foliation carries a natural transverse symplectic form in general [Reference GotayG]. Since the distribution
![]() $T{\mathcal{F}}\subset TQ$
is preserved by Reeb flow, it generates the
$T{\mathcal{F}}\subset TQ$
is preserved by Reeb flow, it generates the
![]() $S^{1}$
-action thereon in the current context. We denote by
$S^{1}$
-action thereon in the current context. We denote by
the projection to
![]() $T{\mathcal{N}}$
and to
$T{\mathcal{N}}$
and to
![]() $G$
, respectively, with respect to the splitting (3.2). We denote by
$G$
, respectively, with respect to the splitting (3.2). We denote by
![]() $T^{\ast }{\mathcal{N}}\rightarrow Q$
the associated foliation cotangent bundle, that is, the dual bundle of
$T^{\ast }{\mathcal{N}}\rightarrow Q$
the associated foliation cotangent bundle, that is, the dual bundle of
![]() $T{\mathcal{N}}$
.
$T{\mathcal{N}}$
.
We now consider the isomorphism
and fix a splitting
![]() $T_{Q}M=TQ\oplus N_{Q}M$
with
$T_{Q}M=TQ\oplus N_{Q}M$
with
![]() $T_{Q}M=TM|_{Q}$
so that
$T_{Q}M=TM|_{Q}$
so that
![]() $N_{Q}M\subset \unicode[STIX]{x1D709}_{Q}$
: this is possible since
$N_{Q}M\subset \unicode[STIX]{x1D709}_{Q}$
: this is possible since
![]() $\mathbb{R}\{X_{\unicode[STIX]{x1D706}}\}\subset TQ$
. We can also choose the splitting so that it is
$\mathbb{R}\{X_{\unicode[STIX]{x1D706}}\}\subset TQ$
. We can also choose the splitting so that it is
![]() $S^{1}$
-equivariant. (See the proof of Proposition 3.9 below.)
$S^{1}$
-equivariant. (See the proof of Proposition 3.9 below.)
This leads to the further splitting
combined with (3.2), which in turn leads to
where
![]() $(\cdot )^{\bot }$
denotes the annihilator of
$(\cdot )^{\bot }$
denotes the annihilator of
![]() $(\cdot )$
. In particular, it induces an isomorphism
$(\cdot )$
. In particular, it induces an isomorphism
Now we consider the embedding
![]() $T^{\ast }{\mathcal{N}}\rightarrow \unicode[STIX]{x1D709}$
defined by the inverse of (3.3), which we denote by
$T^{\ast }{\mathcal{N}}\rightarrow \unicode[STIX]{x1D709}$
defined by the inverse of (3.3), which we denote by
Next we consider the symplectic normal bundle
![]() $(TQ)^{d\unicode[STIX]{x1D706}}\subset T_{Q}M$
defined by
$(TQ)^{d\unicode[STIX]{x1D706}}\subset T_{Q}M$
defined by
We define a vector bundle
and then have the natural embedding
induced by the inclusion map
![]() $(TQ)^{d\unicode[STIX]{x1D706}}{\hookrightarrow}T_{Q}M$
. The following is straightforward to check.
$(TQ)^{d\unicode[STIX]{x1D706}}{\hookrightarrow}T_{Q}M$
. The following is straightforward to check.
Lemma 3.8. The
![]() $d\unicode[STIX]{x1D706}|_{E}$
induces a nondegenerate 2-form and so
$d\unicode[STIX]{x1D706}|_{E}$
induces a nondegenerate 2-form and so
![]() $E$
carries a fiberwise symplectic form, which we denote by
$E$
carries a fiberwise symplectic form, which we denote by
![]() $\unicode[STIX]{x1D6FA}$
.
$\unicode[STIX]{x1D6FA}$
.
We now consider the exact sequence
induced by (3.10). The sequence is
![]() $S^{1}$
-equivariant with respect to the natural
$S^{1}$
-equivariant with respect to the natural
![]() $S^{1}$
-action thereon. We have the canonical isomorphism
$S^{1}$
-action thereon. We have the canonical isomorphism
which is
![]() $S^{1}$
-equivariant. Then we have an
$S^{1}$
-equivariant. Then we have an
![]() $S^{1}$
-equivariant splitting
$S^{1}$
-equivariant splitting
where
![]() $(T{\mathcal{N}})^{\#_{d\unicode[STIX]{x1D706}}}$
is the
$(T{\mathcal{N}})^{\#_{d\unicode[STIX]{x1D706}}}$
is the
![]() $d\unicode[STIX]{x1D706}$
-dual (3.7). This also induces an embedding
$d\unicode[STIX]{x1D706}$
-dual (3.7). This also induces an embedding
which is also
![]() $S^{1}$
-equivariant.
$S^{1}$
-equivariant.
We now denote
![]() $F:=T^{\ast }{\mathcal{N}}\oplus E\rightarrow Q$
. The following proposition provides a local model of the neighborhood of
$F:=T^{\ast }{\mathcal{N}}\oplus E\rightarrow Q$
. The following proposition provides a local model of the neighborhood of
![]() $Q\subset M$
.
$Q\subset M$
.
Proposition 3.9. We fix the splittings (3.2) and (3.4). Then the sum of (3.12) and (3.10) defines an isomorphism
![]() $T^{\ast }{\mathcal{N}}\oplus E\rightarrow N_{Q}M$
depending only on the splittings.
$T^{\ast }{\mathcal{N}}\oplus E\rightarrow N_{Q}M$
depending only on the splittings.
Proof. A straightforward dimension counting shows that the bundle map indeed is an isomorphism. ◻
Identifying a neighborhood of
![]() $Q\subset M$
with a neighborhood of the zero section of
$Q\subset M$
with a neighborhood of the zero section of
![]() $F$
and pulling back the contact form
$F$
and pulling back the contact form
![]() $\unicode[STIX]{x1D706}$
to
$\unicode[STIX]{x1D706}$
to
![]() $F$
, we may assume that our contact form
$F$
, we may assume that our contact form
![]() $\unicode[STIX]{x1D706}$
is defined on a neighborhood of
$\unicode[STIX]{x1D706}$
is defined on a neighborhood of
![]() $o_{F}\subset F$
. We also identify with
$o_{F}\subset F$
. We also identify with
![]() $T^{\ast }{\mathcal{N}}$
and
$T^{\ast }{\mathcal{N}}$
and
![]() $E$
as their images in
$E$
as their images in
![]() $N_{Q}M$
.
$N_{Q}M$
.
Proposition 3.10. The
![]() $S^{1}$
-action on
$S^{1}$
-action on
![]() $Q$
canonically induces the
$Q$
canonically induces the
![]() $S^{1}$
-invariant vector bundle structure on
$S^{1}$
-invariant vector bundle structure on
![]() $E$
such that the form
$E$
such that the form
![]() $\unicode[STIX]{x1D6FA}$
is invariant under the
$\unicode[STIX]{x1D6FA}$
is invariant under the
![]() $S^{1}$
-action on
$S^{1}$
-action on
![]() $E$
.
$E$
.
Proof. The action of
![]() $S^{1}$
on
$S^{1}$
on
![]() $Q$
by
$Q$
by
![]() $t\cdot q=\unicode[STIX]{x1D719}^{t}(q)$
canonically induces a
$t\cdot q=\unicode[STIX]{x1D719}^{t}(q)$
canonically induces a
![]() $S^{1}$
action on
$S^{1}$
action on
![]() $T_{Q}M$
by
$T_{Q}M$
by
![]() $t\cdot v=(d\unicode[STIX]{x1D719}^{t})(v)$
, for
$t\cdot v=(d\unicode[STIX]{x1D719}^{t})(v)$
, for
![]() $v\in T_{Q}M$
. Hence it gives rise to the following identity
$v\in T_{Q}M$
. Hence it gives rise to the following identity
since the Reeb flow preserves
![]() $\unicode[STIX]{x1D706}$
. We first show it is well-defined on
$\unicode[STIX]{x1D706}$
. We first show it is well-defined on
![]() $E\rightarrow Q$
, that is, if
$E\rightarrow Q$
, that is, if
![]() $v\in (T_{q}Q)^{d\unicode[STIX]{x1D706}}$
, then
$v\in (T_{q}Q)^{d\unicode[STIX]{x1D706}}$
, then
![]() $t\cdot v\in (T_{t\cdot q}Q)^{d\unicode[STIX]{x1D706}}$
. In fact, by using (3.13), for
$t\cdot v\in (T_{t\cdot q}Q)^{d\unicode[STIX]{x1D706}}$
. In fact, by using (3.13), for
![]() $w\in T_{t\cdot q}Q$
,
$w\in T_{t\cdot q}Q$
,
This vanishes, since
![]() $Q$
consists of closed Reeb orbits and thus
$Q$
consists of closed Reeb orbits and thus
![]() $d\unicode[STIX]{x1D719}^{t}$
preserves
$d\unicode[STIX]{x1D719}^{t}$
preserves
![]() $TQ$
.
$TQ$
.
Secondly, the same identity (3.13) further indicates that this
![]() $S^{1}$
action preserves
$S^{1}$
action preserves
![]() $\unicode[STIX]{x1D6FA}$
on fibers, that is,
$\unicode[STIX]{x1D6FA}$
on fibers, that is,
![]() $t^{\ast }\unicode[STIX]{x1D6FA}=\unicode[STIX]{x1D6FA}$
, and we are done with the proof of this proposition.◻
$t^{\ast }\unicode[STIX]{x1D6FA}=\unicode[STIX]{x1D6FA}$
, and we are done with the proof of this proposition.◻
Summarizing the above discussion, we have concluded that the base
![]() $Q$
is decorated by the one-form
$Q$
is decorated by the one-form
![]() $\unicode[STIX]{x1D703}:=i_{Q}^{\ast }\unicode[STIX]{x1D706}$
on the base
$\unicode[STIX]{x1D703}:=i_{Q}^{\ast }\unicode[STIX]{x1D706}$
on the base
![]() $Q$
and the bundle
$Q$
and the bundle
![]() $E$
is decorated by the fiberwise symplectic 2-form
$E$
is decorated by the fiberwise symplectic 2-form
![]() $\unicode[STIX]{x1D6FA}$
. They satisfy the following additional properties:
$\unicode[STIX]{x1D6FA}$
. They satisfy the following additional properties:
(1)
 $Q=o_{F}$
carries an
$Q=o_{F}$
carries an
 $S^{1}$
-action which is locally free. In particular
$S^{1}$
-action which is locally free. In particular
 $Q/S^{1}$
is a smooth orbifold;
$Q/S^{1}$
is a smooth orbifold;(2) the one-form
 $\unicode[STIX]{x1D703}$
is
$\unicode[STIX]{x1D703}$
is
 $S^{1}$
-invariant, and
$S^{1}$
-invariant, and
 $d\unicode[STIX]{x1D703}$
is a presymplectic form;
$d\unicode[STIX]{x1D703}$
is a presymplectic form;(3) the bundle
 $E$
carries an
$E$
carries an
 $S^{1}$
-action that preserves the fiberwise 2-form
$S^{1}$
-action that preserves the fiberwise 2-form
 $\unicode[STIX]{x1D6FA}$
and hence induces a
$\unicode[STIX]{x1D6FA}$
and hence induces a
 $S^{1}$
-invariant symplectic vector bundle structure on
$S^{1}$
-invariant symplectic vector bundle structure on
 $E$
;
$E$
;(4) the bundle
 $F=T^{\ast }{\mathcal{N}}\oplus E\rightarrow Q$
carries the direct sum
$F=T^{\ast }{\mathcal{N}}\oplus E\rightarrow Q$
carries the direct sum
 $S^{1}$
-equivariant vector bundle structure compatible to the
$S^{1}$
-equivariant vector bundle structure compatible to the
 $S^{1}$
-action on
$S^{1}$
-action on
 $Q$
.
$Q$
.
We summarize the above discussions into the following theorem.
Theorem 3.11. Consider the locus
![]() $Q$
of closed Reeb orbits of a Morse–Bott-type contact form
$Q$
of closed Reeb orbits of a Morse–Bott-type contact form
![]() $\unicode[STIX]{x1D706}$
. Let
$\unicode[STIX]{x1D706}$
. Let
![]() $(TQ)^{\unicode[STIX]{x1D714}_{Q}}\subset TQ$
be the null distribution of
$(TQ)^{\unicode[STIX]{x1D714}_{Q}}\subset TQ$
be the null distribution of
![]() $\unicode[STIX]{x1D714}_{Q}=i_{Q}^{\ast }d\unicode[STIX]{x1D706}$
and
$\unicode[STIX]{x1D714}_{Q}=i_{Q}^{\ast }d\unicode[STIX]{x1D706}$
and
![]() ${\mathcal{F}}$
be the associated characteristic foliation. Then the restriction of
${\mathcal{F}}$
be the associated characteristic foliation. Then the restriction of
![]() $\unicode[STIX]{x1D706}$
to
$\unicode[STIX]{x1D706}$
to
![]() $Q$
induces the following geometric structures:
$Q$
induces the following geometric structures:
(1)
 $Q=o_{F}$
carries an
$Q=o_{F}$
carries an
 $S^{1}$
-action which is locally free. In particular
$S^{1}$
-action which is locally free. In particular
 $Q/S^{1}$
is a smooth orbifold. Fix an
$Q/S^{1}$
is a smooth orbifold. Fix an
 $S^{1}$
-invariant splitting (3.2);
$S^{1}$
-invariant splitting (3.2);(2) we have the natural identification
(3.14)as an $$\begin{eqnarray}N_{Q}M\cong T^{\ast }{\mathcal{N}}\oplus E=F,\end{eqnarray}$$
$$\begin{eqnarray}N_{Q}M\cong T^{\ast }{\mathcal{N}}\oplus E=F,\end{eqnarray}$$
 $S^{1}$
-equivariant vector bundle, where is the symplectic normal bundle;
$S^{1}$
-equivariant vector bundle, where is the symplectic normal bundle; $$\begin{eqnarray}E:=(TQ)^{d\unicode[STIX]{x1D706}}/T{\mathcal{F}}\end{eqnarray}$$
$$\begin{eqnarray}E:=(TQ)^{d\unicode[STIX]{x1D706}}/T{\mathcal{F}}\end{eqnarray}$$
(3) the two-form
 $d\unicode[STIX]{x1D706}$
restricts to a nondegenerate skew-symmetric two-form on
$d\unicode[STIX]{x1D706}$
restricts to a nondegenerate skew-symmetric two-form on
 $G$
, and induces a fiberwise symplectic form
$G$
, and induces a fiberwise symplectic form
 $\unicode[STIX]{x1D6FA}$
on
$\unicode[STIX]{x1D6FA}$
on
 $E$
defined as above.
$E$
defined as above.
We say that
![]() $Q$
is of prequantization type if the rank of
$Q$
is of prequantization type if the rank of
![]() $d\unicode[STIX]{x1D706}|_{Q}$
is maximal and is of isotropic type if the rank of
$d\unicode[STIX]{x1D706}|_{Q}$
is maximal and is of isotropic type if the rank of
![]() $d\unicode[STIX]{x1D706}|_{Q}$
is zero. The general case will be a mixture of the two.
$d\unicode[STIX]{x1D706}|_{Q}$
is zero. The general case will be a mixture of the two.
Remark 3.12. In particular when
![]() $\dim M=3$
, such
$\dim M=3$
, such
![]() $Q$
must be either of prequantization type or of isotropic type. This is the case that is considered in [Reference Hofer, Wysocki and ZehnderHWZ3]. The general case considered in [Reference BourgeoisBou] and [Reference Bourgeois, Eliashberg, Hofer, Wysocki and ZehnderBEHWZ] includes the mixed type.
$Q$
must be either of prequantization type or of isotropic type. This is the case that is considered in [Reference Hofer, Wysocki and ZehnderHWZ3]. The general case considered in [Reference BourgeoisBou] and [Reference Bourgeois, Eliashberg, Hofer, Wysocki and ZehnderBEHWZ] includes the mixed type.
4 Contact thickening of Morse–Bott contact setup
Motivated by the isomorphism in Theorem 3.11, we consider the pair
![]() $(Q,\unicode[STIX]{x1D703})$
and the symplectic vector bundle
$(Q,\unicode[STIX]{x1D703})$
and the symplectic vector bundle
![]() $(E,\unicode[STIX]{x1D6FA})\rightarrow Q$
that satisfy the above properties. We assume that
$(E,\unicode[STIX]{x1D6FA})\rightarrow Q$
that satisfy the above properties. We assume that
![]() $Q$
is compact and connected.
$Q$
is compact and connected.
In the next section, we associate the model contact form on the direct sum
and prove a canonical neighborhood theorem of the locus of closed Reeb orbits of general contact manifold
![]() $(M,\unicode[STIX]{x1D706})$
such that the zero section of
$(M,\unicode[STIX]{x1D706})$
such that the zero section of
![]() $F$
corresponds to
$F$
corresponds to
![]() $Q$
.
$Q$
.
To state our canonical neighborhood theorem, we need to first identify the relevant geometric structure of the canonical neighborhoods. For this purpose, introduction of the following notion is useful.
Definition 4.1. (Precontact form)
We call a one-form
![]() $\unicode[STIX]{x1D703}$
on a manifold
$\unicode[STIX]{x1D703}$
on a manifold
![]() $Q$
a precontact form if
$Q$
a precontact form if
![]() $d\unicode[STIX]{x1D703}$
has constant rank.
$d\unicode[STIX]{x1D703}$
has constant rank.
4.1 The
 $S^{1}$
-invariant precontact manifold
$S^{1}$
-invariant precontact manifold
 $(Q,\unicode[STIX]{x1D703})$
$(Q,\unicode[STIX]{x1D703})$
First, we consider the pair
![]() $(Q,\unicode[STIX]{x1D703})$
such that
$(Q,\unicode[STIX]{x1D703})$
such that
![]() $Q$
carries a nontrivial
$Q$
carries a nontrivial
![]() $S^{1}$
-action preserving the one-form
$S^{1}$
-action preserving the one-form
![]() $\unicode[STIX]{x1D703}$
. After taking the quotient of
$\unicode[STIX]{x1D703}$
. After taking the quotient of
![]() $S^{1}$
by some finite subgroup, we may assume that the action is effective. We also assume that the action is locally free. Then by the general theory of group actions of compact Lie group (see [Reference HelgasonHe] for example), the action is free on a dense open subset and has only a finite number of different types of isotropy groups. In particular the quotient
$S^{1}$
by some finite subgroup, we may assume that the action is effective. We also assume that the action is locally free. Then by the general theory of group actions of compact Lie group (see [Reference HelgasonHe] for example), the action is free on a dense open subset and has only a finite number of different types of isotropy groups. In particular the quotient
![]() $P:=Q/S^{1}$
becomes a presymplectic orbifold with a finite number of different types of orbifold points. We denote by
$P:=Q/S^{1}$
becomes a presymplectic orbifold with a finite number of different types of orbifold points. We denote by
![]() $Y$
the vector field generating the
$Y$
the vector field generating the
![]() $S^{1}$
-action, that is, the
$S^{1}$
-action, that is, the
![]() $S^{1}$
-action is generated by its flows.
$S^{1}$
-action is generated by its flows.
We require that the circle action preserves
![]() $\unicode[STIX]{x1D703}$
, that is,
$\unicode[STIX]{x1D703}$
, that is,
![]() ${\mathcal{L}}_{Y}\unicode[STIX]{x1D703}=0$
. Since the action is locally free and free on a dense open subset of
${\mathcal{L}}_{Y}\unicode[STIX]{x1D703}=0$
. Since the action is locally free and free on a dense open subset of
![]() $Q$
, we can normalize the action so that
$Q$
, we can normalize the action so that
We denote this normalized vector field by
![]() $X_{\unicode[STIX]{x1D703}}$
. We would like to emphasize that
$X_{\unicode[STIX]{x1D703}}$
. We would like to emphasize that
![]() $\unicode[STIX]{x1D703}$
may not be a contact form but can be regarded as the connection form of the circle bundle
$\unicode[STIX]{x1D703}$
may not be a contact form but can be regarded as the connection form of the circle bundle
![]() $S^{1}\rightarrow Q\rightarrow P$
over the orbifold
$S^{1}\rightarrow Q\rightarrow P$
over the orbifold
![]() $P$
in general. Although
$P$
in general. Although
![]() $P$
may carry nonempty set of orbifold points, the connection form
$P$
may carry nonempty set of orbifold points, the connection form
![]() $\unicode[STIX]{x1D703}$
is assumed to be smooth on
$\unicode[STIX]{x1D703}$
is assumed to be smooth on
![]() $Q$
.
$Q$
.
Similarly as in Lemma 3.7, we also require the presence of
![]() $S^{1}$
-invariant splitting
$S^{1}$
-invariant splitting
such that the subbundle
![]() $H$
is also integrable.
$H$
is also integrable.
With these terminologies introduced, we can rephrase Theorem 3.11 as follows.
Theorem 4.2. Let
![]() $Q$
be the locus foliated by closed Reeb orbits of a contact manifold
$Q$
be the locus foliated by closed Reeb orbits of a contact manifold
![]() $(M,\unicode[STIX]{x1D706})$
of Morse–Bott type. Then
$(M,\unicode[STIX]{x1D706})$
of Morse–Bott type. Then
![]() $Q$
carries a locally free
$Q$
carries a locally free
![]() $S^{1}$
-action and:
$S^{1}$
-action and:
(1) an
 $S^{1}$
-invariant precontact form
$S^{1}$
-invariant precontact form
 $\unicode[STIX]{x1D703}$
given by
$\unicode[STIX]{x1D703}$
given by
 $\unicode[STIX]{x1D703}=i_{Q}^{\ast }\unicode[STIX]{x1D706}$
;
$\unicode[STIX]{x1D703}=i_{Q}^{\ast }\unicode[STIX]{x1D706}$
;(2) a splitting
(4.2)such that the distribution $$\begin{eqnarray}\ker d\unicode[STIX]{x1D703}=\mathbb{R}\{X_{\unicode[STIX]{x1D703}}\}\oplus H,\end{eqnarray}$$
$$\begin{eqnarray}\ker d\unicode[STIX]{x1D703}=\mathbb{R}\{X_{\unicode[STIX]{x1D703}}\}\oplus H,\end{eqnarray}$$
 $H=\ker d\unicode[STIX]{x1D703}\cap \unicode[STIX]{x1D709}|_{Q}$
is integrable;
$H=\ker d\unicode[STIX]{x1D703}\cap \unicode[STIX]{x1D709}|_{Q}$
is integrable;(3) an
 $S^{1}$
-equivariant symplectic vector bundle
$S^{1}$
-equivariant symplectic vector bundle
 $(E,\unicode[STIX]{x1D6FA})\rightarrow Q$
with
$(E,\unicode[STIX]{x1D6FA})\rightarrow Q$
with  $$\begin{eqnarray}E=(TQ)^{d\unicode[STIX]{x1D706}}/\!\ker d\unicode[STIX]{x1D703},\qquad \unicode[STIX]{x1D6FA}=[d\unicode[STIX]{x1D706}]_{E}\end{eqnarray}$$
$$\begin{eqnarray}E=(TQ)^{d\unicode[STIX]{x1D706}}/\!\ker d\unicode[STIX]{x1D703},\qquad \unicode[STIX]{x1D6FA}=[d\unicode[STIX]{x1D706}]_{E}\end{eqnarray}$$
Here we use the fact that there exists a canonical embedding
and
![]() $d\unicode[STIX]{x1D706}|_{(TQ)^{d\unicode[STIX]{x1D706}}}$
canonically induces a bilinear form
$d\unicode[STIX]{x1D706}|_{(TQ)^{d\unicode[STIX]{x1D706}}}$
canonically induces a bilinear form
![]() $[d\unicode[STIX]{x1D706}]_{E}$
on
$[d\unicode[STIX]{x1D706}]_{E}$
on
![]() $E=(TQ)^{d\unicode[STIX]{x1D706}}/\ker di_{Q}^{\ast }\unicode[STIX]{x1D706}$
by symplectic reduction.
$E=(TQ)^{d\unicode[STIX]{x1D706}}/\ker di_{Q}^{\ast }\unicode[STIX]{x1D706}$
by symplectic reduction.
Definition 4.3. Let
![]() $(Q,\unicode[STIX]{x1D703})$
be a precontact manifold equipped with a locally free
$(Q,\unicode[STIX]{x1D703})$
be a precontact manifold equipped with a locally free
![]() $S^{1}$
-action generated by a vector field
$S^{1}$
-action generated by a vector field
![]() $Y$
, and with a
$Y$
, and with a
![]() $S^{1}$
-invariant one-form
$S^{1}$
-invariant one-form
![]() $\unicode[STIX]{x1D703}$
and the splitting (4.2). Assume
$\unicode[STIX]{x1D703}$
and the splitting (4.2). Assume
![]() $\unicode[STIX]{x1D703}(Y)\equiv 1$
. We call such a triple
$\unicode[STIX]{x1D703}(Y)\equiv 1$
. We call such a triple
![]() $(Q,\unicode[STIX]{x1D703},H)$
a Morse–Bott contact setup.
$(Q,\unicode[STIX]{x1D703},H)$
a Morse–Bott contact setup.
As before, we denote by
![]() ${\mathcal{F}}$
and
${\mathcal{F}}$
and
![]() ${\mathcal{N}}$
the associated foliations on
${\mathcal{N}}$
the associated foliations on
![]() $Q$
, and decompose
$Q$
, and decompose
We define a one-form
![]() $\unicode[STIX]{x1D6E9}_{G}$
on
$\unicode[STIX]{x1D6E9}_{G}$
on
![]() $T^{\ast }{\mathcal{N}}$
as follows. For a tangent
$T^{\ast }{\mathcal{N}}$
as follows. For a tangent
![]() $\unicode[STIX]{x1D709}\in T_{\unicode[STIX]{x1D6FC}}(T^{\ast }{\mathcal{N}})$
, define
$\unicode[STIX]{x1D709}\in T_{\unicode[STIX]{x1D6FC}}(T^{\ast }{\mathcal{N}})$
, define
using the splitting
By definition, it follows
![]() $\unicode[STIX]{x1D6E9}_{G}|_{VT(T^{\ast }{\mathcal{N}})}\equiv 0$
and
$\unicode[STIX]{x1D6E9}_{G}|_{VT(T^{\ast }{\mathcal{N}})}\equiv 0$
and
![]() $d\unicode[STIX]{x1D6E9}_{G}(\unicode[STIX]{x1D6FC})$
is nondegenerate on
$d\unicode[STIX]{x1D6E9}_{G}(\unicode[STIX]{x1D6FC})$
is nondegenerate on
which becomes the canonical pairing defined on
![]() $T_{q}{\mathcal{N}}\oplus T_{q}^{\ast }{\mathcal{N}}$
under the identification.
$T_{q}{\mathcal{N}}\oplus T_{q}^{\ast }{\mathcal{N}}$
under the identification.
4.2 The bundle
 $E$
$E$
We next examine the structure of the
![]() $S^{1}$
-equivariant symplectic vector bundle
$S^{1}$
-equivariant symplectic vector bundle
![]() $(E,\unicode[STIX]{x1D6FA})$
.
$(E,\unicode[STIX]{x1D6FA})$
.
We denote by
![]() $\vec{R}$
the radial vector field which generates the family of radial multiplication
$\vec{R}$
the radial vector field which generates the family of radial multiplication
This vector field is invariant under the given
![]() $S^{1}$
-action on
$S^{1}$
-action on
![]() $E$
, and vanishes on the zero section. By its definition,
$E$
, and vanishes on the zero section. By its definition,
![]() $d\unicode[STIX]{x1D70B}(\vec{R})=0$
, that is,
$d\unicode[STIX]{x1D70B}(\vec{R})=0$
, that is,
![]() $\vec{R}$
is in the vertical distribution, denoted by
$\vec{R}$
is in the vertical distribution, denoted by
![]() $VTE$
, of
$VTE$
, of
![]() $TE$
.
$TE$
.
Denote the canonical isomorphism
![]() $V_{e}TE\cong E_{\unicode[STIX]{x1D70B}(e)}$
by
$V_{e}TE\cong E_{\unicode[STIX]{x1D70B}(e)}$
by
![]() $I_{e;\unicode[STIX]{x1D70B}(e)}$
. It obviously intertwines the scalar multiplication, that is,
$I_{e;\unicode[STIX]{x1D70B}(e)}$
. It obviously intertwines the scalar multiplication, that is,
for a scalar
![]() $\unicode[STIX]{x1D707}$
. It also satisfies the following identity (4.4) with respect to the derivative of the fiberwise scalar multiplication map
$\unicode[STIX]{x1D707}$
. It also satisfies the following identity (4.4) with respect to the derivative of the fiberwise scalar multiplication map
![]() $R_{c}:E\rightarrow E$
.
$R_{c}:E\rightarrow E$
.
Lemma 4.4. Let
![]() $\unicode[STIX]{x1D709}\in V_{e}TE$
. Then
$\unicode[STIX]{x1D709}\in V_{e}TE$
. Then
on
![]() $E_{\unicode[STIX]{x1D70B}(c\,e)}=E_{\unicode[STIX]{x1D70B}(e)}$
for any constant
$E_{\unicode[STIX]{x1D70B}(c\,e)}=E_{\unicode[STIX]{x1D70B}(e)}$
for any constant
![]() $c$
.
$c$
.
Proof. We compute
 $$\begin{eqnarray}\displaystyle I_{c\,e;\unicode[STIX]{x1D70B}(c\,e)}(dR_{c}(\unicode[STIX]{x1D709})) & = & \displaystyle \left.I_{c\,e;\unicode[STIX]{x1D70B}(c\,e)}\left(\frac{d}{ds}\right|_{s=0}c(e+s\unicode[STIX]{x1D709})\right)\nonumber\\ \displaystyle & = & \displaystyle I_{c\,e;\unicode[STIX]{x1D70B}(c\,e)}(R_{c}(\unicode[STIX]{x1D709}))=c\,I_{e;\unicode[STIX]{x1D70B}(e)}(\unicode[STIX]{x1D709})\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{c\,e;\unicode[STIX]{x1D70B}(c\,e)}(dR_{c}(\unicode[STIX]{x1D709})) & = & \displaystyle \left.I_{c\,e;\unicode[STIX]{x1D70B}(c\,e)}\left(\frac{d}{ds}\right|_{s=0}c(e+s\unicode[STIX]{x1D709})\right)\nonumber\\ \displaystyle & = & \displaystyle I_{c\,e;\unicode[STIX]{x1D70B}(c\,e)}(R_{c}(\unicode[STIX]{x1D709}))=c\,I_{e;\unicode[STIX]{x1D70B}(e)}(\unicode[STIX]{x1D709})\nonumber\end{eqnarray}$$
which finishes the proof. ◻
We then define the fiberwise two-form
![]() $\unicode[STIX]{x1D6FA}^{v}$
on
$\unicode[STIX]{x1D6FA}^{v}$
on
![]() $VTE\rightarrow E$
by
$VTE\rightarrow E$
by
for
![]() $\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2}\in V_{e}TE$
, and one-form
$\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2}\in V_{e}TE$
, and one-form
![]() $\vec{R}\!\rfloor \unicode[STIX]{x1D6FA}^{v}$
, respectively.
$\vec{R}\!\rfloor \unicode[STIX]{x1D6FA}^{v}$
, respectively.
Now we introduce an
![]() $S^{1}$
-invariant symplectic connection on
$S^{1}$
-invariant symplectic connection on
![]() $E$
and choose the splitting
$E$
and choose the splitting
Existence of such an invariant connection follows for example, by averaging over the compact group
![]() $S^{1}$
. We denote by
$S^{1}$
. We denote by
![]() $\widetilde{\unicode[STIX]{x1D6FA}}$
the resulting two-form on
$\widetilde{\unicode[STIX]{x1D6FA}}$
the resulting two-form on
![]() $E$
. We extend the fiberwise form
$E$
. We extend the fiberwise form
![]() $\unicode[STIX]{x1D6FA}$
of
$\unicode[STIX]{x1D6FA}$
of
![]() $E$
into the differential two-form
$E$
into the differential two-form
![]() $\widetilde{\unicode[STIX]{x1D6FA}}$
on
$\widetilde{\unicode[STIX]{x1D6FA}}$
on
![]() $E$
by setting
$E$
by setting
Denote by
![]() $\vec{R}$
the radial vector field of
$\vec{R}$
the radial vector field of
![]() $E\rightarrow Q$
and consider the one-form
$E\rightarrow Q$
and consider the one-form
which is invariant under the action of
![]() $S^{1}$
on
$S^{1}$
on
![]() $E$
.
$E$
.
Remark 4.5. Suppose
![]() $d\unicode[STIX]{x1D706}_{E}(\cdot ,J_{E}\cdot )=:g_{E;J_{E}}$
defines a Hermitian vector bundle
$d\unicode[STIX]{x1D706}_{E}(\cdot ,J_{E}\cdot )=:g_{E;J_{E}}$
defines a Hermitian vector bundle
![]() $(\unicode[STIX]{x1D709}_{E},g_{E,J},J_{E})$
. Then we can write the radial vector field considered in the previous section as
$(\unicode[STIX]{x1D709}_{E},g_{E,J},J_{E})$
. Then we can write the radial vector field considered in the previous section as
where
![]() $(r_{1},\ldots ,r_{k})$
is the coordinates of
$(r_{1},\ldots ,r_{k})$
is the coordinates of
![]() $e$
for a local frame
$e$
for a local frame
![]() $\{e_{1},\ldots ,e_{k}\}$
of the vector bundle
$\{e_{1},\ldots ,e_{k}\}$
of the vector bundle
![]() $E$
. By definition, we have
$E$
. By definition, we have
Obviously the right-hand side expression does not depend on the choice of local frames. Let
![]() $(E,\unicode[STIX]{x1D6FA},J_{E})$
be a Hermitian vector bundle and define
$(E,\unicode[STIX]{x1D6FA},J_{E})$
be a Hermitian vector bundle and define
![]() $|e|^{2}=g_{F}(e,e)$
. Motivated by the terminology used in [Reference Bott and TuBT], we call the one-form
$|e|^{2}=g_{F}(e,e)$
. Motivated by the terminology used in [Reference Bott and TuBT], we call the one-form
the global angular form for the Hermitian vector bundle
![]() $(E,\unicode[STIX]{x1D6FA},J_{E})$
. Note that
$(E,\unicode[STIX]{x1D6FA},J_{E})$
. Note that
![]() $\unicode[STIX]{x1D713}$
is defined only on
$\unicode[STIX]{x1D713}$
is defined only on
![]() $E\setminus o_{E}$
although
$E\setminus o_{E}$
although
![]() $\unicode[STIX]{x1D6FA}$
is globally defined.
$\unicode[STIX]{x1D6FA}$
is globally defined.
We state the following lemma.
Lemma 4.6. Let
![]() $\unicode[STIX]{x1D6FA}$
be as above. Then:
$\unicode[STIX]{x1D6FA}$
be as above. Then:
(1)
 $\vec{R}\!\rfloor d\widetilde{\unicode[STIX]{x1D6FA}}=0$
;
$\vec{R}\!\rfloor d\widetilde{\unicode[STIX]{x1D6FA}}=0$
;(2) for any nonzero constant
 $c>0$
, we have
$c>0$
, we have  $$\begin{eqnarray}R_{c}^{\ast }\widetilde{\unicode[STIX]{x1D6FA}}=c^{2}\,\widetilde{\unicode[STIX]{x1D6FA}}.\end{eqnarray}$$
$$\begin{eqnarray}R_{c}^{\ast }\widetilde{\unicode[STIX]{x1D6FA}}=c^{2}\,\widetilde{\unicode[STIX]{x1D6FA}}.\end{eqnarray}$$
Proof. Notice that
![]() $\widetilde{\unicode[STIX]{x1D6FA}}$
is compatible with
$\widetilde{\unicode[STIX]{x1D6FA}}$
is compatible with
![]() $\unicode[STIX]{x1D6FA}$
in the sense of symplectic fibration and the symplectic vector bundle connection is nothing but the Ehresmann connection induced by
$\unicode[STIX]{x1D6FA}$
in the sense of symplectic fibration and the symplectic vector bundle connection is nothing but the Ehresmann connection induced by
![]() $\widetilde{\unicode[STIX]{x1D6FA}}$
, which is a symplectic connection now. Since
$\widetilde{\unicode[STIX]{x1D6FA}}$
, which is a symplectic connection now. Since
![]() $\vec{R}$
is vertical, the statement (1) immediately follows from the fact that the symplectic connection is vertical closed.
$\vec{R}$
is vertical, the statement (1) immediately follows from the fact that the symplectic connection is vertical closed.
It remains to prove statement (2). Let
![]() $e\in E$
and
$e\in E$
and
![]() $\unicode[STIX]{x1D709}_{1}$
,
$\unicode[STIX]{x1D709}_{1}$
,
![]() $\unicode[STIX]{x1D709}_{2}\in T_{e}E$
. By definition, we derive
$\unicode[STIX]{x1D709}_{2}\in T_{e}E$
. By definition, we derive
where we use the equality (4.4) and
![]() $\unicode[STIX]{x1D70B}_{F}(c\,e)=\unicode[STIX]{x1D70B}(e)$
for the fourth equality.
$\unicode[STIX]{x1D70B}_{F}(c\,e)=\unicode[STIX]{x1D70B}(e)$
for the fourth equality.
This proves
![]() $R_{c}^{\ast }\widetilde{\unicode[STIX]{x1D6FA}}=c^{2}\widetilde{\unicode[STIX]{x1D6FA}}$
.◻
$R_{c}^{\ast }\widetilde{\unicode[STIX]{x1D6FA}}=c^{2}\widetilde{\unicode[STIX]{x1D6FA}}$
.◻
It follows from Lemma 4.6(2) that we get
![]() ${\mathcal{L}}_{\vec{R}}\widetilde{\unicode[STIX]{x1D6FA}}=2\widetilde{\unicode[STIX]{x1D6FA}}$
. By Cartan’s formula, we get
${\mathcal{L}}_{\vec{R}}\widetilde{\unicode[STIX]{x1D6FA}}=2\widetilde{\unicode[STIX]{x1D6FA}}$
. By Cartan’s formula, we get
4.3 Canonical contact form and contact structure on
 $F$
$F$
Let
![]() $(Q,\unicode[STIX]{x1D703},H)$
be a given Morse–Bott contact setup and
$(Q,\unicode[STIX]{x1D703},H)$
be a given Morse–Bott contact setup and
![]() $(E,\unicode[STIX]{x1D6FA})\rightarrow Q$
be any
$(E,\unicode[STIX]{x1D6FA})\rightarrow Q$
be any
![]() $S^{1}$
-equivariant symplectic vector bundle equipped with an
$S^{1}$
-equivariant symplectic vector bundle equipped with an
![]() $S^{1}$
-invariant symplectic connection on it.
$S^{1}$
-invariant symplectic connection on it.
Now we equip the bundle
![]() $F=T^{\ast }{\mathcal{N}}\oplus E$
with a canonical
$F=T^{\ast }{\mathcal{N}}\oplus E$
with a canonical
![]() $S^{1}$
-invariant contact form on
$S^{1}$
-invariant contact form on
![]() $F$
. We denote the bundle projections by
$F$
. We denote the bundle projections by
![]() $\unicode[STIX]{x1D70B}_{E;F}:F\rightarrow E$
and
$\unicode[STIX]{x1D70B}_{E;F}:F\rightarrow E$
and
![]() $\unicode[STIX]{x1D70B}_{T^{\ast }{\mathcal{N}};F}:F\rightarrow T^{\ast }{\mathcal{N}}$
of the splitting
$\unicode[STIX]{x1D70B}_{T^{\ast }{\mathcal{N}};F}:F\rightarrow T^{\ast }{\mathcal{N}}$
of the splitting
![]() $F=T^{\ast }{\mathcal{N}}\oplus E$
, respectively, and provide the direct sum connection on
$F=T^{\ast }{\mathcal{N}}\oplus E$
, respectively, and provide the direct sum connection on
![]() $F=T^{\ast }{\mathcal{N}}\oplus E$
.
$F=T^{\ast }{\mathcal{N}}\oplus E$
.
Theorem 4.7. Let
![]() $(Q,\unicode[STIX]{x1D703},H)$
be a Morse–Bott contact setup. Denote by
$(Q,\unicode[STIX]{x1D703},H)$
be a Morse–Bott contact setup. Denote by
![]() ${\mathcal{F}}$
and
${\mathcal{F}}$
and
![]() ${\mathcal{N}}$
the foliations associated to the distribution
${\mathcal{N}}$
the foliations associated to the distribution
![]() $\ker d\unicode[STIX]{x1D703}$
and
$\ker d\unicode[STIX]{x1D703}$
and
![]() $H$
, respectively. We also denote by
$H$
, respectively. We also denote by
![]() $T{\mathcal{F}}$
,
$T{\mathcal{F}}$
,
![]() $T{\mathcal{N}}$
the associated foliation tangent bundles and
$T{\mathcal{N}}$
the associated foliation tangent bundles and
![]() $T^{\ast }{\mathcal{N}}$
the foliation cotangent bundle of
$T^{\ast }{\mathcal{N}}$
the foliation cotangent bundle of
![]() ${\mathcal{N}}$
. Then for any symplectic vector bundle
${\mathcal{N}}$
. Then for any symplectic vector bundle
![]() $(E,\unicode[STIX]{x1D6FA})\rightarrow Q$
with an
$(E,\unicode[STIX]{x1D6FA})\rightarrow Q$
with an
![]() $S^{1}$
-invariant symplectic connection, the following holds:
$S^{1}$
-invariant symplectic connection, the following holds:
(1) the total space of the bundle
 $F=T^{\ast }{\mathcal{N}}\oplus E$
carries a canonical contact form
$F=T^{\ast }{\mathcal{N}}\oplus E$
carries a canonical contact form
 $\unicode[STIX]{x1D706}_{F;G}$
defined as in (4.8), for each choice of complement
$\unicode[STIX]{x1D706}_{F;G}$
defined as in (4.8), for each choice of complement
 $G$
such that
$G$
such that
 $TQ=T{\mathcal{F}}\oplus G$
;
$TQ=T{\mathcal{F}}\oplus G$
;(2) for any two such choices of
 $G$
,
$G$
,
 $G^{\prime }$
, the associated contact forms are canonically gauge-equivalent by a bundle map
$G^{\prime }$
, the associated contact forms are canonically gauge-equivalent by a bundle map
 $\unicode[STIX]{x1D713}_{GG^{\prime }}:TQ\rightarrow TQ$
preserving
$\unicode[STIX]{x1D713}_{GG^{\prime }}:TQ\rightarrow TQ$
preserving
 $T{\mathcal{F}}$
.
$T{\mathcal{F}}$
.
Proof. We define a differential one-form on
![]() $F$
explicitly by
$F$
explicitly by
Using Lemma 4.6, we obtain
by taking the differential of (4.8).
A moment of examination of this formula gives rise to the following
Proposition 4.8. There exists some
![]() $\unicode[STIX]{x1D6FF}>0$
such that the one-form
$\unicode[STIX]{x1D6FF}>0$
such that the one-form
![]() $\unicode[STIX]{x1D706}_{F}$
is a contact form on the disc bundle
$\unicode[STIX]{x1D706}_{F}$
is a contact form on the disc bundle
![]() $D^{\unicode[STIX]{x1D6FF}}(F)$
, where
$D^{\unicode[STIX]{x1D6FF}}(F)$
, where
such that
![]() $\unicode[STIX]{x1D706}_{F}|_{o_{F}}=\unicode[STIX]{x1D703}$
on
$\unicode[STIX]{x1D706}_{F}|_{o_{F}}=\unicode[STIX]{x1D703}$
on
![]() $Q\cong o_{F}\subset F$
.
$Q\cong o_{F}\subset F$
.
This proves the statement (1).
For the proof of the statement (2), we first note that the bundle
![]() $E$
itself does not depend on the choice of
$E$
itself does not depend on the choice of
![]() $G$
. On the other hand, we put the one-form
$G$
. On the other hand, we put the one-form
on
![]() $E$
, which depends on
$E$
, which depends on
![]() $G$
in general because the one-form
$G$
in general because the one-form
![]() $\unicode[STIX]{x1D6E9}_{G}$
does. Furthermore, we recall that the projection map
$\unicode[STIX]{x1D6E9}_{G}$
does. Furthermore, we recall that the projection map
![]() $\unicode[STIX]{x1D70B}_{T^{\ast }{\mathcal{N}};F}$
also depends on the canonical splitting
$\unicode[STIX]{x1D70B}_{T^{\ast }{\mathcal{N}};F}$
also depends on the canonical splitting
Now we fix this splitting
![]() $T_{Q}F$
and let
$T_{Q}F$
and let
![]() $G$
,
$G$
,
![]() $G^{\prime }$
be two splittings of
$G^{\prime }$
be two splittings of
![]() $TQ$
$TQ$
Since both
![]() $G$
,
$G$
,
![]() $G^{\prime }$
are transversal to
$G^{\prime }$
are transversal to
![]() $T{\mathcal{F}}$
in
$T{\mathcal{F}}$
in
![]() $TQ$
, we can represent
$TQ$
, we can represent
![]() $G^{\prime }$
as the graph of the bundle map
$G^{\prime }$
as the graph of the bundle map
![]() $A_{G}:G\rightarrow T{\mathcal{N}}$
. Then we consider the bundle isomorphism
$A_{G}:G\rightarrow T{\mathcal{N}}$
. Then we consider the bundle isomorphism
defined by
under the splitting
![]() $TQ=\mathbb{R}\{X_{\unicode[STIX]{x1D706}}\}\oplus T{\mathcal{N}}\oplus G$
. Then
$TQ=\mathbb{R}\{X_{\unicode[STIX]{x1D706}}\}\oplus T{\mathcal{N}}\oplus G$
. Then
![]() $\unicode[STIX]{x1D713}_{GG^{\prime }}(G)=\text{Graph}\,A_{G}$
and
$\unicode[STIX]{x1D713}_{GG^{\prime }}(G)=\text{Graph}\,A_{G}$
and
![]() $\unicode[STIX]{x1D713}_{GG^{\prime }}|_{T{\mathcal{N}}}=\operatorname{id}_{T{\mathcal{N}}}$
. Therefore, we have
$\unicode[STIX]{x1D713}_{GG^{\prime }}|_{T{\mathcal{N}}}=\operatorname{id}_{T{\mathcal{N}}}$
. Therefore, we have
![]() $p_{T{\mathcal{N}};G}=p_{T{\mathcal{N}};G^{\prime }}\circ \unicode[STIX]{x1D713}_{GG^{\prime }}$
.
$p_{T{\mathcal{N}};G}=p_{T{\mathcal{N}};G^{\prime }}\circ \unicode[STIX]{x1D713}_{GG^{\prime }}$
.
We compute
This proves
![]() $\unicode[STIX]{x1D6E9}_{G}=\unicode[STIX]{x1D6E9}_{G^{\prime }}\circ \unicode[STIX]{x1D713}_{GG^{\prime }}$
.◻
$\unicode[STIX]{x1D6E9}_{G}=\unicode[STIX]{x1D6E9}_{G^{\prime }}\circ \unicode[STIX]{x1D713}_{GG^{\prime }}$
.◻
Now we study the contact geometry of
![]() $(D^{\unicode[STIX]{x1D6FF}}(F),\unicode[STIX]{x1D706}_{F})$
. We first note that the two-form
$(D^{\unicode[STIX]{x1D6FF}}(F),\unicode[STIX]{x1D706}_{F})$
. We first note that the two-form
![]() $d\unicode[STIX]{x1D706}_{F}$
is a presymplectic form with one-dimensional kernel such that
$d\unicode[STIX]{x1D706}_{F}$
is a presymplectic form with one-dimensional kernel such that
Denote by
![]() $\widetilde{X}:=(d\unicode[STIX]{x1D70B}_{F;H})^{-1}(X)$
the horizontal lifting of the vector field
$\widetilde{X}:=(d\unicode[STIX]{x1D70B}_{F;H})^{-1}(X)$
the horizontal lifting of the vector field
![]() $X$
on
$X$
on
![]() $Q$
, where
$Q$
, where
is the bijection of the horizontal distribution and
![]() $TQ$
.
$TQ$
.
Lemma 4.9. (Reeb vector field)
The Reeb vector field
![]() $X_{F}$
of
$X_{F}$
of
![]() $\unicode[STIX]{x1D706}_{F}$
is given by
$\unicode[STIX]{x1D706}_{F}$
is given by
where
![]() $\widetilde{X}_{\unicode[STIX]{x1D703}}$
denotes the horizontal lifting of
$\widetilde{X}_{\unicode[STIX]{x1D703}}$
denotes the horizontal lifting of
![]() $X_{\unicode[STIX]{x1D703}}$
to
$X_{\unicode[STIX]{x1D703}}$
to
![]() $F$
.
$F$
.
Proof. We only have to check the defining property
![]() $\widetilde{X}_{\unicode[STIX]{x1D703}}\!\rfloor \unicode[STIX]{x1D706}_{F}=1$
and
$\widetilde{X}_{\unicode[STIX]{x1D703}}\!\rfloor \unicode[STIX]{x1D706}_{F}=1$
and
![]() $\widetilde{X}_{\unicode[STIX]{x1D703}}\!\rfloor d\unicode[STIX]{x1D706}_{F}=0$
. We first look at
$\widetilde{X}_{\unicode[STIX]{x1D703}}\!\rfloor d\unicode[STIX]{x1D706}_{F}=0$
. We first look at
Here
![]() $\widetilde{\unicode[STIX]{x1D6FA}}(\vec{R},\widetilde{X}_{\unicode[STIX]{x1D703}})=0$
by definition of
$\widetilde{\unicode[STIX]{x1D6FA}}(\vec{R},\widetilde{X}_{\unicode[STIX]{x1D703}})=0$
by definition of
![]() $\widetilde{\unicode[STIX]{x1D6FA}}$
since
$\widetilde{\unicode[STIX]{x1D6FA}}$
since
![]() $\widetilde{X}_{\unicode[STIX]{x1D703}}^{v}=0$
. Then we calculate
$\widetilde{X}_{\unicode[STIX]{x1D703}}^{v}=0$
. Then we calculate
We only need to explain why the last term
![]() $\widetilde{X}_{\unicode[STIX]{x1D703}}\!\rfloor \unicode[STIX]{x1D70B}_{T^{\ast }{\mathcal{N}};F}^{\ast }\,d\unicode[STIX]{x1D6E9}_{G}$
vanishes. In fact
$\widetilde{X}_{\unicode[STIX]{x1D703}}\!\rfloor \unicode[STIX]{x1D70B}_{T^{\ast }{\mathcal{N}};F}^{\ast }\,d\unicode[STIX]{x1D6E9}_{G}$
vanishes. In fact
![]() $pr_{{\mathcal{N}};G}\,d\unicode[STIX]{x1D70B}_{F}(\widetilde{X}_{\unicode[STIX]{x1D703}})=pr_{{\mathcal{N}};G}(X_{\unicode[STIX]{x1D703}})=0$
. Using this, the definition of
$pr_{{\mathcal{N}};G}\,d\unicode[STIX]{x1D70B}_{F}(\widetilde{X}_{\unicode[STIX]{x1D703}})=pr_{{\mathcal{N}};G}(X_{\unicode[STIX]{x1D703}})=0$
. Using this, the definition of
![]() $\unicode[STIX]{x1D6E9}_{G}$
and the
$\unicode[STIX]{x1D6E9}_{G}$
and the
![]() $S^{1}$
-equivariance of the vector bundle
$S^{1}$
-equivariance of the vector bundle
![]() $F\rightarrow Q$
and the fact that
$F\rightarrow Q$
and the fact that
![]() $\widetilde{X}_{\unicode[STIX]{x1D703}}$
is the vector field generating the
$\widetilde{X}_{\unicode[STIX]{x1D703}}$
is the vector field generating the
![]() $S^{1}$
-action, we derive
$S^{1}$
-action, we derive
by a straightforward computation. This finishes the proof. ◻
Now we calculate the contact structure
![]() $\unicode[STIX]{x1D709}_{F}$
.
$\unicode[STIX]{x1D709}_{F}$
.
Lemma 4.10. (Contact distribution)
At each point
![]() $(\unicode[STIX]{x1D6FC},e)\in U_{F}\subset F$
, we define two subspaces of
$(\unicode[STIX]{x1D6FC},e)\in U_{F}\subset F$
, we define two subspaces of
![]() $T_{(\unicode[STIX]{x1D6FC},e)}F$
$T_{(\unicode[STIX]{x1D6FC},e)}F$
and
Then
![]() $\unicode[STIX]{x1D709}_{F}=V\oplus W$
.
$\unicode[STIX]{x1D709}_{F}=V\oplus W$
.
Proof. By straightforward calculation, both
![]() $V$
and
$V$
and
![]() $W$
are subspaces of
$W$
are subspaces of
![]() $\unicode[STIX]{x1D709}_{F}=\ker \unicode[STIX]{x1D706}_{F}$
.
$\unicode[STIX]{x1D709}_{F}=\ker \unicode[STIX]{x1D706}_{F}$
.
For any
![]() $\unicode[STIX]{x1D709}\in \unicode[STIX]{x1D709}_{F}$
, we decompose
$\unicode[STIX]{x1D709}\in \unicode[STIX]{x1D709}_{F}$
, we decompose
![]() $\unicode[STIX]{x1D709}=\unicode[STIX]{x1D709}^{\text{h}}+\unicode[STIX]{x1D709}^{\text{v}}$
using the decomposition
$\unicode[STIX]{x1D709}=\unicode[STIX]{x1D709}^{\text{h}}+\unicode[STIX]{x1D709}^{\text{v}}$
using the decomposition
![]() $TF=HTF\oplus VTF$
. Since
$TF=HTF\oplus VTF$
. Since
![]() $\unicode[STIX]{x1D70B}_{T^{\ast }{\mathcal{N}};F}^{\ast }\unicode[STIX]{x1D6E9}_{G}(\widetilde{\unicode[STIX]{x1D702}})=\unicode[STIX]{x1D6E9}_{G}(\unicode[STIX]{x1D702})$
and we can write
$\unicode[STIX]{x1D70B}_{T^{\ast }{\mathcal{N}};F}^{\ast }\unicode[STIX]{x1D6E9}_{G}(\widetilde{\unicode[STIX]{x1D702}})=\unicode[STIX]{x1D6E9}_{G}(\unicode[STIX]{x1D702})$
and we can write
![]() $\unicode[STIX]{x1D709}^{\text{v}}=I_{(e;\unicode[STIX]{x1D70B}(e))}(v)$
for a unique
$\unicode[STIX]{x1D709}^{\text{v}}=I_{(e;\unicode[STIX]{x1D70B}(e))}(v)$
for a unique
![]() $v\in E_{\unicode[STIX]{x1D70B}(e)}$
. Therefore, we need to find
$v\in E_{\unicode[STIX]{x1D70B}(e)}$
. Therefore, we need to find
![]() $b\in \mathbb{R}$
,
$b\in \mathbb{R}$
,
![]() $\unicode[STIX]{x1D702}\in \ker \unicode[STIX]{x1D703}$
so that for the horizontal vector
$\unicode[STIX]{x1D702}\in \ker \unicode[STIX]{x1D703}$
so that for the horizontal vector
![]() $\unicode[STIX]{x1D709}^{\text{h}}=\widetilde{(\unicode[STIX]{x1D702}+bX_{\unicode[STIX]{x1D703}})}$
$\unicode[STIX]{x1D709}^{\text{h}}=\widetilde{(\unicode[STIX]{x1D702}+bX_{\unicode[STIX]{x1D703}})}$
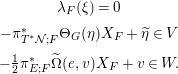 $$\begin{eqnarray}\displaystyle & \unicode[STIX]{x1D706}_{F}(\unicode[STIX]{x1D709})=0 & \displaystyle \nonumber\\ \displaystyle & -\unicode[STIX]{x1D70B}_{T^{\ast }{\mathcal{N}};F}^{\ast }\unicode[STIX]{x1D6E9}_{G}(\unicode[STIX]{x1D702})X_{F}+\widetilde{\unicode[STIX]{x1D702}}\in V & \displaystyle \nonumber\\ \displaystyle & -{\textstyle \frac{1}{2}}\unicode[STIX]{x1D70B}_{E;F}^{\ast }\widetilde{\unicode[STIX]{x1D6FA}}(e,v)X_{F}+v\in W. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \unicode[STIX]{x1D706}_{F}(\unicode[STIX]{x1D709})=0 & \displaystyle \nonumber\\ \displaystyle & -\unicode[STIX]{x1D70B}_{T^{\ast }{\mathcal{N}};F}^{\ast }\unicode[STIX]{x1D6E9}_{G}(\unicode[STIX]{x1D702})X_{F}+\widetilde{\unicode[STIX]{x1D702}}\in V & \displaystyle \nonumber\\ \displaystyle & -{\textstyle \frac{1}{2}}\unicode[STIX]{x1D70B}_{E;F}^{\ast }\widetilde{\unicode[STIX]{x1D6FA}}(e,v)X_{F}+v\in W. & \displaystyle \nonumber\end{eqnarray}$$
Then
which determines
![]() $\unicode[STIX]{x1D702}\in T_{\unicode[STIX]{x1D70B}(e)}{\mathcal{N}}\oplus G_{\unicode[STIX]{x1D70B}(e)}$
uniquely. We need to determine
$\unicode[STIX]{x1D702}\in T_{\unicode[STIX]{x1D70B}(e)}{\mathcal{N}}\oplus G_{\unicode[STIX]{x1D70B}(e)}$
uniquely. We need to determine
![]() $b$
.
$b$
.
Since
 $$\begin{eqnarray}\displaystyle 0=\unicode[STIX]{x1D706}_{F}(\unicode[STIX]{x1D709}) & = & \displaystyle \unicode[STIX]{x1D706}_{F}(\widetilde{\unicode[STIX]{x1D702}}+bX_{F}+\unicode[STIX]{x1D709}^{\text{v}})\nonumber\\ \displaystyle & = & \displaystyle b+\unicode[STIX]{x1D706}_{F}(\widetilde{\unicode[STIX]{x1D702}})+\unicode[STIX]{x1D706}_{F}(\unicode[STIX]{x1D709}^{\text{v}})\nonumber\\ \displaystyle & = & \displaystyle b+\unicode[STIX]{x1D70B}_{T^{\ast }{\mathcal{N}};F}^{\ast }\unicode[STIX]{x1D6E9}_{G}(\widetilde{\unicode[STIX]{x1D702}})+{\textstyle \frac{1}{2}}\unicode[STIX]{x1D70B}_{E;F}^{\ast }\widetilde{\unicode[STIX]{x1D6FA}}(e,v).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0=\unicode[STIX]{x1D706}_{F}(\unicode[STIX]{x1D709}) & = & \displaystyle \unicode[STIX]{x1D706}_{F}(\widetilde{\unicode[STIX]{x1D702}}+bX_{F}+\unicode[STIX]{x1D709}^{\text{v}})\nonumber\\ \displaystyle & = & \displaystyle b+\unicode[STIX]{x1D706}_{F}(\widetilde{\unicode[STIX]{x1D702}})+\unicode[STIX]{x1D706}_{F}(\unicode[STIX]{x1D709}^{\text{v}})\nonumber\\ \displaystyle & = & \displaystyle b+\unicode[STIX]{x1D70B}_{T^{\ast }{\mathcal{N}};F}^{\ast }\unicode[STIX]{x1D6E9}_{G}(\widetilde{\unicode[STIX]{x1D702}})+{\textstyle \frac{1}{2}}\unicode[STIX]{x1D70B}_{E;F}^{\ast }\widetilde{\unicode[STIX]{x1D6FA}}(e,v).\nonumber\end{eqnarray}$$
Then we set
![]() $\unicode[STIX]{x1D709}_{W}=-(1/2)\unicode[STIX]{x1D70B}_{E;F}^{\ast }\widetilde{\unicode[STIX]{x1D6FA}}(\vec{R},v)X_{F}+v$
for
$\unicode[STIX]{x1D709}_{W}=-(1/2)\unicode[STIX]{x1D70B}_{E;F}^{\ast }\widetilde{\unicode[STIX]{x1D6FA}}(\vec{R},v)X_{F}+v$
for
![]() $v$
such that
$v$
such that
![]() $I_{e;\unicode[STIX]{x1D70B}(e)}(v)=\unicode[STIX]{x1D709}^{v}$
and then finally choose
$I_{e;\unicode[STIX]{x1D70B}(e)}(v)=\unicode[STIX]{x1D709}^{v}$
and then finally choose
![]() $b=-\unicode[STIX]{x1D70B}_{T^{\ast }{\mathcal{N}};F}^{\ast }\unicode[STIX]{x1D6E9}_{G}(\widetilde{\unicode[STIX]{x1D702}})$
so that
$b=-\unicode[STIX]{x1D70B}_{T^{\ast }{\mathcal{N}};F}^{\ast }\unicode[STIX]{x1D6E9}_{G}(\widetilde{\unicode[STIX]{x1D702}})$
so that
![]() $\unicode[STIX]{x1D709}_{V}:=-\unicode[STIX]{x1D70B}_{T^{\ast }{\mathcal{N}};F}^{\ast }\unicode[STIX]{x1D6E9}_{G}(\widetilde{\unicode[STIX]{x1D702}})X_{F}+\widetilde{\unicode[STIX]{x1D702}}$
. Therefore, we have proved
$\unicode[STIX]{x1D709}_{V}:=-\unicode[STIX]{x1D70B}_{T^{\ast }{\mathcal{N}};F}^{\ast }\unicode[STIX]{x1D6E9}_{G}(\widetilde{\unicode[STIX]{x1D702}})X_{F}+\widetilde{\unicode[STIX]{x1D702}}$
. Therefore, we have proved
![]() $\unicode[STIX]{x1D709}_{F}=V+W$
.
$\unicode[STIX]{x1D709}_{F}=V+W$
.
To see it is a direct sum, assume
for some
![]() $\unicode[STIX]{x1D702}\in \unicode[STIX]{x1D709}_{\unicode[STIX]{x1D706}}$
and
$\unicode[STIX]{x1D702}\in \unicode[STIX]{x1D709}_{\unicode[STIX]{x1D706}}$
and
![]() $v\in VTM$
. Apply
$v\in VTM$
. Apply
![]() $d\unicode[STIX]{x1D70B}$
to both sides, and it follows that
$d\unicode[STIX]{x1D70B}$
to both sides, and it follows that
Hence
![]() $\unicode[STIX]{x1D702}=0$
, and then
$\unicode[STIX]{x1D702}=0$
, and then
![]() $v=0$
follows since
$v=0$
follows since
![]() $X_{F}$
is in horizontal part. This finishes the proof.◻
$X_{F}$
is in horizontal part. This finishes the proof.◻
5 Canonical neighborhoods of the locus of closed Reeb orbits
Now let
![]() $Q$
be the submanifold of
$Q$
be the submanifold of
![]() $(M,\unicode[STIX]{x1D706})$
that is foliated by the closed Reeb orbits of
$(M,\unicode[STIX]{x1D706})$
that is foliated by the closed Reeb orbits of
![]() $\unicode[STIX]{x1D706}$
with constant period
$\unicode[STIX]{x1D706}$
with constant period
![]() $T$
. Consider the Morse–Bott contact setup
$T$
. Consider the Morse–Bott contact setup
![]() $(Q,\unicode[STIX]{x1D703},H)$
defined as before and the symplectic vector bundle
$(Q,\unicode[STIX]{x1D703},H)$
defined as before and the symplectic vector bundle
![]() $(E,\unicode[STIX]{x1D6FA})$
associated to
$(E,\unicode[STIX]{x1D6FA})$
associated to
![]() $Q$
.
$Q$
.
Now in this section, we prove the following canonical neighborhood theorem as the converse of Theorem 4.2.
Theorem 5.1. (Canonical neighborhood theorem)
Let
![]() $Q$
be the submanifold of closed Reeb orbits of Morse–Bott-type contact form
$Q$
be the submanifold of closed Reeb orbits of Morse–Bott-type contact form
![]() $\unicode[STIX]{x1D706}$
, and
$\unicode[STIX]{x1D706}$
, and
![]() $(Q,\unicode[STIX]{x1D703})$
and
$(Q,\unicode[STIX]{x1D703})$
and
![]() $(E,\unicode[STIX]{x1D6FA})$
be the associated pair and
$(E,\unicode[STIX]{x1D6FA})$
be the associated pair and
![]() $F=T^{\ast }{\mathcal{N}}\oplus E$
defined above. Then there exist neighborhoods
$F=T^{\ast }{\mathcal{N}}\oplus E$
defined above. Then there exist neighborhoods
![]() $U$
of
$U$
of
![]() $Q$
and
$Q$
and
![]() $U_{F}$
of the zero section
$U_{F}$
of the zero section
![]() $o_{F}$
, and a diffeomorphism
$o_{F}$
, and a diffeomorphism
![]() $\unicode[STIX]{x1D713}:U_{F}\rightarrow U$
and a function
$\unicode[STIX]{x1D713}:U_{F}\rightarrow U$
and a function
![]() $f:U_{F}\rightarrow \mathbb{R}$
such that
$f:U_{F}\rightarrow \mathbb{R}$
such that
and
where we use the canonical identification of
![]() $VTF|_{o_{F}}\cong T^{\ast }{\mathcal{N}}\oplus E$
on the zero section
$VTF|_{o_{F}}\cong T^{\ast }{\mathcal{N}}\oplus E$
on the zero section
![]() $o_{F}\cong Q$
.
$o_{F}\cong Q$
.
We first identify the local pair
![]() $({\mathcal{U}},Q)\cong (U_{F},Q)$
by a diffeomorphism
$({\mathcal{U}},Q)\cong (U_{F},Q)$
by a diffeomorphism
![]() $\unicode[STIX]{x1D719}:{\mathcal{U}}\rightarrow U_{F}$
such that
$\unicode[STIX]{x1D719}:{\mathcal{U}}\rightarrow U_{F}$
such that
Such a diffeomorphism obviously exists by definition of
![]() $E$
and
$E$
and
![]() $T^{\ast }{\mathcal{N}}$
via the normal exponential map with respect to any metric
$T^{\ast }{\mathcal{N}}$
via the normal exponential map with respect to any metric
![]() $g$
(defined on
$g$
(defined on
![]() ${\mathcal{U}}$
) that satisfies the following property: we note that we have the associated short exact sequences
${\mathcal{U}}$
) that satisfies the following property: we note that we have the associated short exact sequences
which are
![]() $S^{1}$
-equivariant with respect to the above mentioned natural induced
$S^{1}$
-equivariant with respect to the above mentioned natural induced
![]() $S^{1}$
-action on
$S^{1}$
-action on
![]() $Q$
. We take
$Q$
. We take
![]() $S^{1}$
-equivariant splittings of (5.2), (5.3) in addition to that of (5.1) used in Theorem 1.6. We then choose an
$S^{1}$
-equivariant splittings of (5.2), (5.3) in addition to that of (5.1) used in Theorem 1.6. We then choose an
![]() $S^{1}$
-equivariant metric on the vector bundle
$S^{1}$
-equivariant metric on the vector bundle
![]() $N_{Q}M\cong F$
whose associated normal exponential map of
$N_{Q}M\cong F$
whose associated normal exponential map of
![]() $Q\cong o_{F}$
respects the above chosen splittings.
$Q\cong o_{F}$
respects the above chosen splittings.
From now on, we sometimes denote
![]() $U_{F}$
by
$U_{F}$
by
![]() $F$
in the following context if there is no danger of confusion. Now
$F$
in the following context if there is no danger of confusion. Now
![]() $F$
carries two contact forms
$F$
carries two contact forms
![]() $\unicode[STIX]{x1D713}^{\ast }\unicode[STIX]{x1D706}$
,
$\unicode[STIX]{x1D713}^{\ast }\unicode[STIX]{x1D706}$
,
![]() $\unicode[STIX]{x1D706}_{F}$
with
$\unicode[STIX]{x1D706}_{F}$
with
![]() $\unicode[STIX]{x1D713}=\unicode[STIX]{x1D719}^{-1}$
and they are the same on the zero section
$\unicode[STIX]{x1D713}=\unicode[STIX]{x1D719}^{-1}$
and they are the same on the zero section
![]() $o_{F}$
. With this preparation, we derive Theorem 5.1 by the following general submanifold version of Gray’s theorem.
$o_{F}$
. With this preparation, we derive Theorem 5.1 by the following general submanifold version of Gray’s theorem.
Theorem 5.2. Let
![]() $M$
be an odd-dimensional manifold with two contact forms
$M$
be an odd-dimensional manifold with two contact forms
![]() $\unicode[STIX]{x1D706}_{0}$
and
$\unicode[STIX]{x1D706}_{0}$
and
![]() $\unicode[STIX]{x1D706}_{1}$
on it. Let
$\unicode[STIX]{x1D706}_{1}$
on it. Let
![]() $Q$
be a closed manifold of closed Reeb orbits of
$Q$
be a closed manifold of closed Reeb orbits of
![]() $\unicode[STIX]{x1D706}_{0}$
in
$\unicode[STIX]{x1D706}_{0}$
in
![]() $M$
and
$M$
and
where we denote
![]() $T_{Q}M=TM|_{Q}$
. Then there exists a diffeomorphism
$T_{Q}M=TM|_{Q}$
. Then there exists a diffeomorphism
![]() $\unicode[STIX]{x1D719}$
from a neighborhood
$\unicode[STIX]{x1D719}$
from a neighborhood
![]() ${\mathcal{U}}$
to
${\mathcal{U}}$
to
![]() ${\mathcal{V}}$
such that
${\mathcal{V}}$
such that
and a function
![]() $f>0$
such that
$f>0$
such that
and
Proof. By the assumption on
![]() $\unicode[STIX]{x1D706}_{0}$
,
$\unicode[STIX]{x1D706}_{0}$
,
![]() $\unicode[STIX]{x1D706}_{1}$
, there exists a small tubular neighborhood of
$\unicode[STIX]{x1D706}_{1}$
, there exists a small tubular neighborhood of
![]() $Q$
in
$Q$
in
![]() $M$
, denote by
$M$
, denote by
![]() ${\mathcal{U}}$
, such that the isotopy
${\mathcal{U}}$
, such that the isotopy
![]() $\unicode[STIX]{x1D706}_{t}=(1-t)\unicode[STIX]{x1D706}_{0}+t\unicode[STIX]{x1D706}_{1}$
,
$\unicode[STIX]{x1D706}_{t}=(1-t)\unicode[STIX]{x1D706}_{0}+t\unicode[STIX]{x1D706}_{1}$
,
![]() $t\in [0,1]$
, are contact forms in
$t\in [0,1]$
, are contact forms in
![]() ${\mathcal{U}}$
: this follows from the requirement (5.4). Moreover, we have
${\mathcal{U}}$
: this follows from the requirement (5.4). Moreover, we have
Then the standard Moser’s trick will finish up the proof. For reader’s convenience, we provide the details here.
We are looking for a family of diffeomorphisms onto its image
![]() $\unicode[STIX]{x1D719}_{t}:{\mathcal{U}}^{\prime }\rightarrow {\mathcal{U}}$
for some smaller open subset
$\unicode[STIX]{x1D719}_{t}:{\mathcal{U}}^{\prime }\rightarrow {\mathcal{U}}$
for some smaller open subset
![]() ${\mathcal{U}}^{\prime }\subset \overline{{\mathcal{U}}^{\prime }}\subset {\mathcal{U}}$
such that
${\mathcal{U}}^{\prime }\subset \overline{{\mathcal{U}}^{\prime }}\subset {\mathcal{U}}$
such that
for all
![]() $t\in [0,1]$
, together with a family of functions
$t\in [0,1]$
, together with a family of functions
![]() $f_{t}>0$
defined on
$f_{t}>0$
defined on
![]() $\overline{{\mathcal{U}}^{\prime }}$
such that
$\overline{{\mathcal{U}}^{\prime }}$
such that
for
![]() $0\leqslant t\leqslant 1$
. We further require
$0\leqslant t\leqslant 1$
. We further require
![]() $f_{t}\equiv 1$
on
$f_{t}\equiv 1$
on
![]() $Q$
and
$Q$
and
![]() $df_{t}|_{Q}\equiv 0$
.
$df_{t}|_{Q}\equiv 0$
.
Since
![]() $Q$
is a closed manifold, it is enough to look for the vector fields
$Q$
is a closed manifold, it is enough to look for the vector fields
![]() $Y_{t}$
generating
$Y_{t}$
generating
![]() $\unicode[STIX]{x1D719}_{t}$
via
$\unicode[STIX]{x1D719}_{t}$
via
that satisfies
 $$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}\unicode[STIX]{x1D719}_{t}^{\ast }\left({\displaystyle \frac{d}{dt}}\unicode[STIX]{x1D706}_{t}+{\mathcal{L}}_{Y_{t}}\unicode[STIX]{x1D706}_{t}\right)={\displaystyle \frac{f_{t}^{\prime }}{f_{t}}}\unicode[STIX]{x1D719}_{t}^{\ast }\unicode[STIX]{x1D706}_{t}\quad \\ Y_{t}|_{Q}\equiv 0,\qquad \unicode[STIX]{x1D6FB}Y_{t}|_{T_{Q}M}\equiv 0.\quad \end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}\unicode[STIX]{x1D719}_{t}^{\ast }\left({\displaystyle \frac{d}{dt}}\unicode[STIX]{x1D706}_{t}+{\mathcal{L}}_{Y_{t}}\unicode[STIX]{x1D706}_{t}\right)={\displaystyle \frac{f_{t}^{\prime }}{f_{t}}}\unicode[STIX]{x1D719}_{t}^{\ast }\unicode[STIX]{x1D706}_{t}\quad \\ Y_{t}|_{Q}\equiv 0,\qquad \unicode[STIX]{x1D6FB}Y_{t}|_{T_{Q}M}\equiv 0.\quad \end{array}\right.\end{eqnarray}$$
By Cartan’s magic formula, the first equation gives rise to
where
Now, we need to show that there exists
![]() $Y_{t}$
such that
$Y_{t}$
such that
![]() $(d/dt)\unicode[STIX]{x1D706}_{t}+{\mathcal{L}}_{Y_{t}}\unicode[STIX]{x1D706}_{t}$
is proportional to
$(d/dt)\unicode[STIX]{x1D706}_{t}+{\mathcal{L}}_{Y_{t}}\unicode[STIX]{x1D706}_{t}$
is proportional to
![]() $\unicode[STIX]{x1D706}_{t}$
. Actually, we can make our choice of
$\unicode[STIX]{x1D706}_{t}$
. Actually, we can make our choice of
![]() $Y_{t}$
unique if we restrict ourselves to those tangent to
$Y_{t}$
unique if we restrict ourselves to those tangent to
![]() $\unicode[STIX]{x1D709}_{t}=\ker \unicode[STIX]{x1D706}_{t}$
by Lemma 2.1.
$\unicode[STIX]{x1D709}_{t}=\ker \unicode[STIX]{x1D706}_{t}$
by Lemma 2.1.
We require
![]() $Y_{t}\in \unicode[STIX]{x1D709}_{t}$
and then (5.8) becomes
$Y_{t}\in \unicode[STIX]{x1D709}_{t}$
and then (5.8) becomes
This in turn determines
![]() $\unicode[STIX]{x1D719}_{t}$
by integration. Since
$\unicode[STIX]{x1D719}_{t}$
by integration. Since
![]() $\unicode[STIX]{x1D6FC}|_{Q}=(\unicode[STIX]{x1D706}_{1}-\unicode[STIX]{x1D706}_{0})|_{Q}=0$
and
$\unicode[STIX]{x1D6FC}|_{Q}=(\unicode[STIX]{x1D706}_{1}-\unicode[STIX]{x1D706}_{0})|_{Q}=0$
and
![]() $\unicode[STIX]{x1D706}_{t}|_{T_{Q}M}=\unicode[STIX]{x1D706}_{0}|_{T_{Q}M}$
, (and hence
$\unicode[STIX]{x1D706}_{t}|_{T_{Q}M}=\unicode[STIX]{x1D706}_{0}|_{T_{Q}M}$
, (and hence
![]() $f_{t}\equiv 1$
on
$f_{t}\equiv 1$
on
![]() $Q$
), it follows that
$Q$
), it follows that
![]() $Y_{t}=0$
on
$Y_{t}=0$
on
![]() $Q$
. Therefore, by compactness of
$Q$
. Therefore, by compactness of
![]() $[0,1]\times Q$
, the domain of existence of the ODE
$[0,1]\times Q$
, the domain of existence of the ODE
![]() ${\dot{x}}=Y_{t}(x)$
includes an open neighborhood of
${\dot{x}}=Y_{t}(x)$
includes an open neighborhood of
![]() $[0,1]\times Q\subset \mathbb{R}\times M$
which we may assume is of the form
$[0,1]\times Q\subset \mathbb{R}\times M$
which we may assume is of the form
![]() $(-\unicode[STIX]{x1D716},1+\unicode[STIX]{x1D716})\times {\mathcal{V}}$
.
$(-\unicode[STIX]{x1D716},1+\unicode[STIX]{x1D716})\times {\mathcal{V}}$
.
Now going back to (5.9), we find that the coefficient
![]() $f_{t}^{\prime }/f_{t}\circ \unicode[STIX]{x1D719}_{t}^{-1}$
is uniquely determined. We evaluate
$f_{t}^{\prime }/f_{t}\circ \unicode[STIX]{x1D719}_{t}^{-1}$
is uniquely determined. We evaluate
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D706}_{1}-\unicode[STIX]{x1D706}_{0}$
against the vector fields
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D706}_{1}-\unicode[STIX]{x1D706}_{0}$
against the vector fields
![]() $X_{t}:=(\unicode[STIX]{x1D719}_{t})_{\ast }X_{\unicode[STIX]{x1D706}_{0}}$
, and get
$X_{t}:=(\unicode[STIX]{x1D719}_{t})_{\ast }X_{\unicode[STIX]{x1D706}_{0}}$
, and get
which determines
![]() $f_{t}$
by integration with the initial condition
$f_{t}$
by integration with the initial condition
![]() $f_{0}\equiv 1$
.
$f_{0}\equiv 1$
.
It remains to check the additional properties (5.5), (5.6). We set
Lemma 5.3.
Proof. By (5.10), we obtain
Since
![]() $X_{t}=X_{\unicode[STIX]{x1D706}_{0}}=X_{\unicode[STIX]{x1D706}_{1}}$
on
$X_{t}=X_{\unicode[STIX]{x1D706}_{0}}=X_{\unicode[STIX]{x1D706}_{1}}$
on
![]() $Q$
,
$Q$
,
![]() $X_{t}\in \unicode[STIX]{x1D709}_{1}\cap \unicode[STIX]{x1D709}_{0}$
and so the second term vanishes.
$X_{t}\in \unicode[STIX]{x1D709}_{1}\cap \unicode[STIX]{x1D709}_{0}$
and so the second term vanishes.
For the first term, consider
![]() $p\in Q$
and
$p\in Q$
and
![]() $v\in T_{p}M$
. Let
$v\in T_{p}M$
. Let
![]() $Y$
be a locally defined vector field with
$Y$
be a locally defined vector field with
![]() $Y(p)=v$
. Then we compute
$Y(p)=v$
. Then we compute
The second term of the right-hand side vanishes since
![]() $\unicode[STIX]{x1D706}_{1}=\unicode[STIX]{x1D706}_{0}$
on
$\unicode[STIX]{x1D706}_{1}=\unicode[STIX]{x1D706}_{0}$
on
![]() $T_{p}M$
for
$T_{p}M$
for
![]() $p\in Q$
. For the first one, we note
$p\in Q$
. For the first one, we note
![]() $X_{t}$
is tangent to
$X_{t}$
is tangent to
![]() $Q$
for all
$Q$
for all
![]() $t$
and
$t$
and
![]() $(\unicode[STIX]{x1D706}_{1}-\unicode[STIX]{x1D706}_{0})(Y)\equiv 0$
on
$(\unicode[STIX]{x1D706}_{1}-\unicode[STIX]{x1D706}_{0})(Y)\equiv 0$
on
![]() $Q$
by the hypothesis
$Q$
by the hypothesis
![]() $\unicode[STIX]{x1D706}_{0}=\unicode[STIX]{x1D706}_{1}$
on
$\unicode[STIX]{x1D706}_{0}=\unicode[STIX]{x1D706}_{1}$
on
![]() $T_{Q}M$
. Therefore, the first term also vanishes. This finishes the proof.◻
$T_{Q}M$
. Therefore, the first term also vanishes. This finishes the proof.◻
Now we set
![]() $g_{t}=\log f_{t}$
. Since
$g_{t}=\log f_{t}$
. Since
![]() $\unicode[STIX]{x1D719}_{t}$
is a diffeomorphism and
$\unicode[STIX]{x1D719}_{t}$
is a diffeomorphism and
![]() $\unicode[STIX]{x1D719}_{t}(Q)\subset Q$
, this implies
$\unicode[STIX]{x1D719}_{t}(Q)\subset Q$
, this implies
![]() $dg_{t}^{\prime }=0$
on
$dg_{t}^{\prime }=0$
on
![]() $Q$
for all
$Q$
for all
![]() $t$
. By integrating
$t$
. By integrating
![]() $dg_{t}^{\prime }=0$
with
$dg_{t}^{\prime }=0$
with
![]() $dg_{0}^{\prime }=0$
along
$dg_{0}^{\prime }=0$
along
![]() $Q$
over time
$Q$
over time
![]() $t=0$
to
$t=0$
to
![]() $t=1$
, which implies
$t=1$
, which implies
![]() $dg_{t}=0$
along
$dg_{t}=0$
along
![]() $Q$
(meaning
$Q$
(meaning
![]() $dg_{t}|_{T_{Q}M}=0$
), that is,
$dg_{t}|_{T_{Q}M}=0$
), that is,
![]() $df_{t}=0$
on
$df_{t}=0$
on
![]() $Q$
. This completes the proof of Theorem 5.2.◻
$Q$
. This completes the proof of Theorem 5.2.◻
Applying this theorem to
![]() $\unicode[STIX]{x1D706}$
and
$\unicode[STIX]{x1D706}$
and
![]() $\unicode[STIX]{x1D706}_{F}$
on
$\unicode[STIX]{x1D706}_{F}$
on
![]() $F$
with
$F$
with
![]() $Q$
as the zero section
$Q$
as the zero section
![]() $o_{F}$
, we can wrap up the proof of Theorem 5.1
$o_{F}$
, we can wrap up the proof of Theorem 5.1
Proof of Theorem 5.1.
The requirement (1.4) and the first of (1.5) are immediate translations of Theorem 5.2. For the second requirement in (1.5), we compute
By using
![]() $df|_{o_{F}}=0$
and
$df|_{o_{F}}=0$
and
![]() $f|_{o_{F}}=1$
, we derive
$f|_{o_{F}}=1$
, we derive
on
![]() $o_{F}$
. This then finishes the second an hence finishes the proof.◻
$o_{F}$
. This then finishes the second an hence finishes the proof.◻
Definition 5.4. (Normal form of contact form)
We call
![]() $(U_{F},f\,\unicode[STIX]{x1D706}_{F})$
the normal form of the contact form
$(U_{F},f\,\unicode[STIX]{x1D706}_{F})$
the normal form of the contact form
![]() $\unicode[STIX]{x1D706}$
associated to the Morse–Bott submanifold
$\unicode[STIX]{x1D706}$
associated to the Morse–Bott submanifold
![]() $Q$
of closed Reeb orbits.
$Q$
of closed Reeb orbits.
Note that the contact structures associated to
![]() $\unicode[STIX]{x1D713}^{\ast }\unicode[STIX]{x1D706}$
and
$\unicode[STIX]{x1D713}^{\ast }\unicode[STIX]{x1D706}$
and
![]() $\unicode[STIX]{x1D706}_{F}$
are the same which is given by
$\unicode[STIX]{x1D706}_{F}$
are the same which is given by
This proves the following normal form theorem of the contact structure
![]() $(M,\unicode[STIX]{x1D709})$
in a neighborhood of
$(M,\unicode[STIX]{x1D709})$
in a neighborhood of
![]() $Q$
.
$Q$
.
Proposition 5.5. Suppose that
![]() $Q\subset M$
be a submanifold of closed Reeb orbits of
$Q\subset M$
be a submanifold of closed Reeb orbits of
![]() $\unicode[STIX]{x1D706}$
. Then there exists a contactomorphism from a neighborhood
$\unicode[STIX]{x1D706}$
. Then there exists a contactomorphism from a neighborhood
![]() ${\mathcal{U}}\supset Q$
to a neighborhood of the zero section of
${\mathcal{U}}\supset Q$
to a neighborhood of the zero section of
![]() $F$
equipped with
$F$
equipped with
![]() $S^{1}$
-equivariant contact structure
$S^{1}$
-equivariant contact structure
![]() $\unicode[STIX]{x1D706}_{F}$
.
$\unicode[STIX]{x1D706}_{F}$
.
Definition 5.6. (Normal form of contact structure)
We call
![]() $(F,\unicode[STIX]{x1D709}_{F})$
the normal form of
$(F,\unicode[STIX]{x1D709}_{F})$
the normal form of
![]() $(M,\unicode[STIX]{x1D709})$
associated to the Morse–Bott submanifold
$(M,\unicode[STIX]{x1D709})$
associated to the Morse–Bott submanifold
![]() $Q$
of closed Reeb orbits.
$Q$
of closed Reeb orbits.
However, the Reeb vector fields of
![]() $\unicode[STIX]{x1D713}^{\ast }\unicode[STIX]{x1D706}$
and
$\unicode[STIX]{x1D713}^{\ast }\unicode[STIX]{x1D706}$
and
![]() $\unicode[STIX]{x1D706}_{F}$
coincide only along the zero section in general.
$\unicode[STIX]{x1D706}_{F}$
coincide only along the zero section in general.
In the rest of the paper, we work with
![]() $F$
and for the general contact form
$F$
and for the general contact form
![]() $\unicode[STIX]{x1D706}$
that satisfies
$\unicode[STIX]{x1D706}$
that satisfies
In particular
![]() $o_{F}$
is also the locus of closed Reeb orbits with the same period
$o_{F}$
is also the locus of closed Reeb orbits with the same period
![]() $T$
of a Morse–Bott contact form
$T$
of a Morse–Bott contact form
![]() $\unicode[STIX]{x1D706}$
. We restate the above normal form theorem in this context.
$\unicode[STIX]{x1D706}$
. We restate the above normal form theorem in this context.
Proposition 5.7. Let
![]() $\unicode[STIX]{x1D706}$
be any contact form in a neighborhood of
$\unicode[STIX]{x1D706}$
be any contact form in a neighborhood of
![]() $o_{F}$
on
$o_{F}$
on
![]() $F$
satisfying (5.11). Then there exist an open embedding
$F$
satisfying (5.11). Then there exist an open embedding
![]() $\unicode[STIX]{x1D713}:{\mathcal{U}}\rightarrow F$
and a function
$\unicode[STIX]{x1D713}:{\mathcal{U}}\rightarrow F$
and a function
![]() $f$
on
$f$
on
![]() ${\mathcal{U}}$
for open neighborhoods
${\mathcal{U}}$
for open neighborhoods
![]() ${\mathcal{U}}$
,
${\mathcal{U}}$
,
![]() $F$
of
$F$
of
![]() $o_{F}$
such that
$o_{F}$
such that
![]() $\unicode[STIX]{x1D713}|_{oF}=\operatorname{id}_{o_{F}}$
,
$\unicode[STIX]{x1D713}|_{oF}=\operatorname{id}_{o_{F}}$
,
![]() $\unicode[STIX]{x1D713}^{\ast }\unicode[STIX]{x1D706}=f\,\unicode[STIX]{x1D706}_{F}$
with
$\unicode[STIX]{x1D713}^{\ast }\unicode[STIX]{x1D706}=f\,\unicode[STIX]{x1D706}_{F}$
with
![]() $f|_{o_{F}}\equiv 1$
and
$f|_{o_{F}}\equiv 1$
and
![]() $df|_{o_{F}}\equiv 0$
.
$df|_{o_{F}}\equiv 0$
.
We denote
![]() $\unicode[STIX]{x1D709}$
and
$\unicode[STIX]{x1D709}$
and
![]() $X_{\unicode[STIX]{x1D706}}$
the corresponding contact structure and Reeb vector field of
$X_{\unicode[STIX]{x1D706}}$
the corresponding contact structure and Reeb vector field of
![]() $\unicode[STIX]{x1D706}$
, and
$\unicode[STIX]{x1D706}$
, and
![]() $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}$
,
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}$
,
![]() $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}_{F}}$
the corresponding projection from
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}_{F}}$
the corresponding projection from
![]() $TF$
to
$TF$
to
![]() $\unicode[STIX]{x1D709}$
and
$\unicode[STIX]{x1D709}$
and
![]() $\unicode[STIX]{x1D709}_{F}$
.
$\unicode[STIX]{x1D709}_{F}$
.
6 Linearization of closed Reeb orbit on the normal form
In this section, we systematically examine the decomposition of the linearization map of closed Reeb orbits in terms of the coordinate expression of the loops
![]() $z$
in
$z$
in
![]() $F$
in this normal neighborhood.
$F$
in this normal neighborhood.
For a given map
![]() $z:S^{1}\rightarrow F$
, we denote by
$z:S^{1}\rightarrow F$
, we denote by
![]() $x:=\unicode[STIX]{x1D70B}_{F}\circ z$
. Then we can express
$x:=\unicode[STIX]{x1D70B}_{F}\circ z$
. Then we can express
where
![]() $s(t)\in F_{x(t)}$
, that is,
$s(t)\in F_{x(t)}$
, that is,
![]() $s$
is the section of
$s$
is the section of
![]() $x^{\ast }F$
.
$x^{\ast }F$
.
We regard this decomposition as the map
where
![]() ${\mathcal{H}}^{F}$
is the infinite-dimensional vector bundle
${\mathcal{H}}^{F}$
is the infinite-dimensional vector bundle
where
![]() ${\mathcal{H}}_{S^{1},x}^{F}$
is the vector space given by
${\mathcal{H}}_{S^{1},x}^{F}$
is the vector space given by
the set of smooth sections of the pullback vector bundle
![]() $x^{\ast }F$
. This provides a coordinate description of
$x^{\ast }F$
. This provides a coordinate description of
![]() $C^{\infty }(S^{1},F)$
in terms of
$C^{\infty }(S^{1},F)$
in terms of
![]() ${\mathcal{H}}_{S^{1}}^{F}$
. We denote the corresponding coordinates
${\mathcal{H}}_{S^{1}}^{F}$
. We denote the corresponding coordinates
![]() $z=(u_{z},s_{z})$
when we feel necessary to make the dependence of
$z=(u_{z},s_{z})$
when we feel necessary to make the dependence of
![]() $(x,s)$
on
$(x,s)$
on
![]() $z$
explicit.
$z$
explicit.
We fix an
![]() $S^{1}$
-invariant connection on
$S^{1}$
-invariant connection on
![]() $F$
and the associated splitting
$F$
and the associated splitting
which is defined to be the direct sum of the connection of
![]() $T^{\ast }{\mathcal{N}}$
and the
$T^{\ast }{\mathcal{N}}$
and the
![]() $S^{1}$
-invariant connection on the symplectic vector bundle
$S^{1}$
-invariant connection on the symplectic vector bundle
![]() $(E,\unicode[STIX]{x1D6FA})$
. Then we express
$(E,\unicode[STIX]{x1D6FA})$
. Then we express
Here we regard
![]() ${\dot{x}}$
as a
${\dot{x}}$
as a
![]() $TQ$
-valued one-form on
$TQ$
-valued one-form on
![]() $S^{1}$
and
$S^{1}$
and
![]() $\unicode[STIX]{x1D6FB}_{t}s$
is defined to be
$\unicode[STIX]{x1D6FB}_{t}s$
is defined to be
which we regard as an element of
![]() $F_{x(t)}$
. Through identification of
$F_{x(t)}$
. Through identification of
![]() $H_{s}TF$
with
$H_{s}TF$
with
![]() $T_{\unicode[STIX]{x1D70B}_{F}(s)}Q$
and
$T_{\unicode[STIX]{x1D70B}_{F}(s)}Q$
and
![]() $V_{s}TF$
with
$V_{s}TF$
with
![]() $F_{\unicode[STIX]{x1D70B}(s)}$
or more precisely through the identity
$F_{\unicode[STIX]{x1D70B}(s)}$
or more precisely through the identity
we just write
Recall that
![]() $o_{F}$
is foliated by the closed Reeb orbits of
$o_{F}$
is foliated by the closed Reeb orbits of
![]() $\unicode[STIX]{x1D706}$
which also form the fibers of the prequantization bundle
$\unicode[STIX]{x1D706}$
which also form the fibers of the prequantization bundle
![]() $Q\rightarrow P$
.
$Q\rightarrow P$
.
For a given Reeb orbit
![]() $z=(x,s)$
, we denote
$z=(x,s)$
, we denote
![]() $x(t)=\unicode[STIX]{x1D6FE}(T\cdot t)$
where
$x(t)=\unicode[STIX]{x1D6FE}(T\cdot t)$
where
![]() $\unicode[STIX]{x1D6FE}$
is a Reeb orbit of period
$\unicode[STIX]{x1D6FE}$
is a Reeb orbit of period
![]() $T$
of the contact form
$T$
of the contact form
![]() $\unicode[STIX]{x1D703}$
on
$\unicode[STIX]{x1D703}$
on
![]() $Q$
which is nothing but a fiber of the prequantization
$Q$
which is nothing but a fiber of the prequantization
![]() $Q\rightarrow P$
. We then decompose
$Q\rightarrow P$
. We then decompose
Then the assignment
![]() $Z\mapsto (D\unicode[STIX]{x1D6F6}(z)(Z))^{v}$
defines an operator from
$Z\mapsto (D\unicode[STIX]{x1D6F6}(z)(Z))^{v}$
defines an operator from
![]() $\unicode[STIX]{x1D6E4}(z^{\ast }VTF)$
to
$\unicode[STIX]{x1D6E4}(z^{\ast }VTF)$
to
![]() $\unicode[STIX]{x1D6E4}(z^{\ast }VTF)$
. We remark that since
$\unicode[STIX]{x1D6E4}(z^{\ast }VTF)$
. We remark that since
![]() $VTF\subset \unicode[STIX]{x1D709}$
, we have
$VTF\subset \unicode[STIX]{x1D709}$
, we have
for any vertical vector field
![]() $Z$
.
$Z$
.
Composing with the map
![]() $I_{z;x}$
, we have obtained an operator from
$I_{z;x}$
, we have obtained an operator from
![]() $\unicode[STIX]{x1D6FA}^{0}(x^{\ast }F)$
to
$\unicode[STIX]{x1D6FA}^{0}(x^{\ast }F)$
to
![]() $\unicode[STIX]{x1D6FA}^{0}(x^{\ast }F)$
. We denote this operator by
$\unicode[STIX]{x1D6FA}^{0}(x^{\ast }F)$
. We denote this operator by
Using
![]() $X_{F}=\widetilde{X}_{\unicode[STIX]{x1D706},Q}$
and
$X_{F}=\widetilde{X}_{\unicode[STIX]{x1D706},Q}$
and
![]() $\unicode[STIX]{x1D6FB}_{Y}X_{F}=0$
for any vertical vector field
$\unicode[STIX]{x1D6FB}_{Y}X_{F}=0$
for any vertical vector field
![]() $Y$
, we derive the following proposition from Lemma 2.8. This will be important later for our exponential estimates.
$Y$
, we derive the following proposition from Lemma 2.8. This will be important later for our exponential estimates.
Proposition 6.1. Let
![]() $D\unicode[STIX]{x1D710}=D\unicode[STIX]{x1D710}(x)$
be the operator defined above. Define the vertical Hamiltonian vector field
$D\unicode[STIX]{x1D710}=D\unicode[STIX]{x1D710}(x)$
be the operator defined above. Define the vertical Hamiltonian vector field
![]() $X_{g}^{\unicode[STIX]{x1D6FA}}$
by
$X_{g}^{\unicode[STIX]{x1D6FA}}$
by
Then
where
![]() $z=(x,o_{x})$
.
$z=(x,o_{x})$
.
Proof. Consider a vertical vector field
![]() $Z\in VTF$
along a Reeb orbit
$Z\in VTF$
along a Reeb orbit
![]() $z$
as above and regard it as the section of
$z$
as above and regard it as the section of
![]() $z^{\ast }F$
defined by
$z^{\ast }F$
defined by
where
![]() $\unicode[STIX]{x1D6FE}$
is a Reeb orbit with period
$\unicode[STIX]{x1D6FE}$
is a Reeb orbit with period
![]() $T$
of
$T$
of
![]() $X_{\unicode[STIX]{x1D706},Q}$
on
$X_{\unicode[STIX]{x1D706},Q}$
on
![]() $o_{F}\cong Q$
. Recall the formula
$o_{F}\cong Q$
. Recall the formula
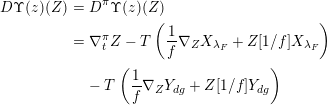 $$\begin{eqnarray}\displaystyle D\unicode[STIX]{x1D6F6}(z)(Z) & = & \displaystyle D^{\unicode[STIX]{x1D70B}}\unicode[STIX]{x1D6F6}(z)(Z)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FB}_{t}^{\unicode[STIX]{x1D70B}}Z-T\left(\frac{1}{f}\unicode[STIX]{x1D6FB}_{Z}X_{\unicode[STIX]{x1D706}_{F}}+Z[1/f]X_{\unicode[STIX]{x1D706}_{F}}\right)\nonumber\\ \displaystyle & & \displaystyle -\,T\left(\frac{1}{f}\unicode[STIX]{x1D6FB}_{Z}Y_{dg}+Z[1/f]Y_{dg}\right)\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle D\unicode[STIX]{x1D6F6}(z)(Z) & = & \displaystyle D^{\unicode[STIX]{x1D70B}}\unicode[STIX]{x1D6F6}(z)(Z)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FB}_{t}^{\unicode[STIX]{x1D70B}}Z-T\left(\frac{1}{f}\unicode[STIX]{x1D6FB}_{Z}X_{\unicode[STIX]{x1D706}_{F}}+Z[1/f]X_{\unicode[STIX]{x1D706}_{F}}\right)\nonumber\\ \displaystyle & & \displaystyle -\,T\left(\frac{1}{f}\unicode[STIX]{x1D6FB}_{Z}Y_{dg}+Z[1/f]Y_{dg}\right)\end{eqnarray}$$
from (6.2), and Lemma 2.8 which we apply to the vertical vector field
![]() $Z$
for the contact manifold
$Z$
for the contact manifold
![]() $(U_{F},\unicode[STIX]{x1D706}_{F})$
.
$(U_{F},\unicode[STIX]{x1D706}_{F})$
.
We recall
![]() $f\equiv 1$
on
$f\equiv 1$
on
![]() $o_{F}$
and
$o_{F}$
and
![]() $df\equiv 0$
on
$df\equiv 0$
on
![]() $TF|_{o_{F}}$
. Therefore, we have
$TF|_{o_{F}}$
. Therefore, we have
![]() $Z[1/f]=0$
. Furthermore, recall
$Z[1/f]=0$
. Furthermore, recall
![]() $X_{F}=\widetilde{X}_{\unicode[STIX]{x1D706},Q}$
and
$X_{F}=\widetilde{X}_{\unicode[STIX]{x1D706},Q}$
and
on
![]() $o_{F}$
. On the other hand, by definition, we derive
$o_{F}$
. On the other hand, by definition, we derive
By substituting this into (6.5) and composing with
![]() $I_{z;x}$
, we have finished the proof.◻
$I_{z;x}$
, we have finished the proof.◻
By construction, it follows that the vector field along
![]() $z$
defined by
$z$
defined by
for any
![]() $v\in T_{z(0)}Q$
lie in
$v\in T_{z(0)}Q$
lie in
![]() $\ker D\unicode[STIX]{x1D6F6}(z)$
. By the Morse–Bott hypothesis, this set of vector fields exhausts
$\ker D\unicode[STIX]{x1D6F6}(z)$
. By the Morse–Bott hypothesis, this set of vector fields exhausts
![]() $\ker D\unicode[STIX]{x1D6F6}(z)$
. We denote by
$\ker D\unicode[STIX]{x1D6F6}(z)$
. We denote by
![]() $\unicode[STIX]{x1D6FF}>0$
the gap between 0 and the first nonzero eigenvalue of
$\unicode[STIX]{x1D6FF}>0$
the gap between 0 and the first nonzero eigenvalue of
![]() $D\unicode[STIX]{x1D6F6}(z)$
. Then we obtain the following
$D\unicode[STIX]{x1D6F6}(z)$
. Then we obtain the following
Corollary 6.2. Let
![]() $z=(x_{z},o_{x_{z}})$
be a Reeb orbit. Then for any section
$z=(x_{z},o_{x_{z}})$
be a Reeb orbit. Then for any section
![]() $s\in \unicode[STIX]{x1D6FA}^{0}(x^{\ast }F)$
, we have
$s\in \unicode[STIX]{x1D6FA}^{0}(x^{\ast }F)$
, we have
This inequality plays a crucial role in the study of exponential convergence of contact instantons in the Morse–Bott context studied later in the present paper.
7 Normal coordinates of
 $dw$
in
$dw$
in
 $(U_{F},f\unicode[STIX]{x1D706}_{F})$
$(U_{F},f\unicode[STIX]{x1D706}_{F})$
We fix the splitting
![]() $TF=HTF\oplus VTF$
given in (6.1) and consider the decomposition of
$TF=HTF\oplus VTF$
given in (6.1) and consider the decomposition of
![]() $w=(u,s)$
according to the splitting. For a given map
$w=(u,s)$
according to the splitting. For a given map
![]() $w:\dot{\unicode[STIX]{x1D6F4}}\rightarrow F$
, we denote by
$w:\dot{\unicode[STIX]{x1D6F4}}\rightarrow F$
, we denote by
![]() $u:=\unicode[STIX]{x1D70B}_{F}\circ w$
. Then we can express
$u:=\unicode[STIX]{x1D70B}_{F}\circ w$
. Then we can express
where
![]() $s(z)\in F_{u(z)}$
, that is,
$s(z)\in F_{u(z)}$
, that is,
![]() $s$
is the section of
$s$
is the section of
![]() $u^{\ast }F$
.
$u^{\ast }F$
.
We regard this decomposition as the map
where
![]() ${\mathcal{H}}^{F}$
is the infinite-dimensional vector bundle
${\mathcal{H}}^{F}$
is the infinite-dimensional vector bundle
where
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D6F4},u}^{F}$
is the vector space given by
${\mathcal{H}}_{\unicode[STIX]{x1D6F4},u}^{F}$
is the vector space given by
the set of smooth sections of the pullback vector bundle
![]() $u^{\ast }F$
. This provides a coordinate description of
$u^{\ast }F$
. This provides a coordinate description of
![]() ${\mathcal{F}}(\unicode[STIX]{x1D6F4},F)$
in terms of
${\mathcal{F}}(\unicode[STIX]{x1D6F4},F)$
in terms of
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D6F4}}^{F}$
. We denote the corresponding coordinates
${\mathcal{H}}_{\unicode[STIX]{x1D6F4}}^{F}$
. We denote the corresponding coordinates
![]() $w=(u_{w},s_{w})$
when we feel necessary to make the dependence of
$w=(u_{w},s_{w})$
when we feel necessary to make the dependence of
![]() $(u,s)$
on
$(u,s)$
on
![]() $w$
explicit.
$w$
explicit.
In terms of the splitting (6.1), we express
Here we regard
![]() $du$
as a
$du$
as a
![]() $TQ$
-valued one-form on
$TQ$
-valued one-form on
![]() $\dot{\unicode[STIX]{x1D6F4}}$
and
$\dot{\unicode[STIX]{x1D6F4}}$
and
![]() $\unicode[STIX]{x1D6FB}_{du}s$
is defined to be
$\unicode[STIX]{x1D6FB}_{du}s$
is defined to be
for a tangent vector
![]() $\unicode[STIX]{x1D702}\in T_{z}\unicode[STIX]{x1D6F4}$
, which we regard as an element of
$\unicode[STIX]{x1D702}\in T_{z}\unicode[STIX]{x1D6F4}$
, which we regard as an element of
![]() $F_{u(z)}$
. Through identification of
$F_{u(z)}$
. Through identification of
![]() $HTF_{s}$
with
$HTF_{s}$
with
![]() $T_{\unicode[STIX]{x1D70B}_{F}(s)}Q$
and
$T_{\unicode[STIX]{x1D70B}_{F}(s)}Q$
and
![]() $VTF_{s}$
with
$VTF_{s}$
with
![]() $F_{\unicode[STIX]{x1D70B}_{F}(s)}$
or more precisely through the identity
$F_{\unicode[STIX]{x1D70B}_{F}(s)}$
or more precisely through the identity
we just write
from now on, unless it is necessary to emphasize the fact that
![]() $dw$
a priori has values in
$dw$
a priori has values in
![]() $TF=HTF\oplus VTF$
, not
$TF=HTF\oplus VTF$
, not
![]() $TQ\oplus F$
.
$TQ\oplus F$
.
To write them in terms of the coordinates
![]() $w=(u,s)$
, we first derive the formula for the projection
$w=(u,s)$
, we first derive the formula for the projection
![]() $d^{\unicode[STIX]{x1D70B}}w=d^{\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}}w$
with
$d^{\unicode[STIX]{x1D70B}}w=d^{\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}}w$
with
![]() $\unicode[STIX]{x1D706}=f\,\unicode[STIX]{x1D706}_{F}$
. For this purpose, we recall the formula for
$\unicode[STIX]{x1D706}=f\,\unicode[STIX]{x1D706}_{F}$
. For this purpose, we recall the formula for
![]() $X_{f\unicode[STIX]{x1D706}_{F}}$
from Proposition 2.6 in Section 2.2
$X_{f\unicode[STIX]{x1D706}_{F}}$
from Proposition 2.6 in Section 2.2
for
![]() $g=\log f$
. We decompose
$g=\log f$
. We decompose
into the vertical and the horizontal components. This leads us to the decomposition
in terms of the splitting
Recalling
![]() $d\unicode[STIX]{x1D706}_{F}=\unicode[STIX]{x1D70B}_{F}^{\ast }d\unicode[STIX]{x1D703}+\unicode[STIX]{x1D70B}_{T^{\ast }{\mathcal{N}};F}^{\ast }d\unicode[STIX]{x1D6E9}_{G}+\unicode[STIX]{x1D70B}_{E;F}^{\ast }\widetilde{\unicode[STIX]{x1D6FA}}$
, and since
$d\unicode[STIX]{x1D706}_{F}=\unicode[STIX]{x1D70B}_{F}^{\ast }d\unicode[STIX]{x1D703}+\unicode[STIX]{x1D70B}_{T^{\ast }{\mathcal{N}};F}^{\ast }d\unicode[STIX]{x1D6E9}_{G}+\unicode[STIX]{x1D70B}_{E;F}^{\ast }\widetilde{\unicode[STIX]{x1D6FA}}$
, and since
![]() $d\unicode[STIX]{x1D6E9}_{G}$
vanishes on
$d\unicode[STIX]{x1D6E9}_{G}$
vanishes on
![]() $VTF$
, we have derived
$VTF$
, we have derived
Lemma 7.1. At each
![]() $s\in F$
,
$s\in F$
,
Now we are ready to derive an important formula that will play a crucial role in our exponential estimates in later sections. Recalling the canonical isomorphism
we introduced in Section 2, we define the following vertical derivative.
Definition 7.2. Let
![]() $X$
be a vector field on
$X$
be a vector field on
![]() $F\rightarrow Q$
. The vertical derivative, denoted by
$F\rightarrow Q$
. The vertical derivative, denoted by
![]() $D^{v}X:F\rightarrow F$
is the map defined by
$D^{v}X:F\rightarrow F$
is the map defined by
Proposition 7.3. Let
![]() $(E,\unicode[STIX]{x1D6FA},J_{E})$
be the Hermitian vector bundle for
$(E,\unicode[STIX]{x1D6FA},J_{E})$
be the Hermitian vector bundle for
![]() $\unicode[STIX]{x1D6FA}$
defined as before. Let
$\unicode[STIX]{x1D6FA}$
defined as before. Let
![]() $g=\log f$
and
$g=\log f$
and
![]() $X_{g}^{d\unicode[STIX]{x1D706}_{E}}$
be the contact Hamiltonian vector field as above. Then we have
$X_{g}^{d\unicode[STIX]{x1D706}_{E}}$
be the contact Hamiltonian vector field as above. Then we have
In particular,
![]() $J_{E}D^{v}X_{g}^{d\unicode[STIX]{x1D706}_{E}}:E\rightarrow E$
is a symmetric endomorphism with respect to the metric
$J_{E}D^{v}X_{g}^{d\unicode[STIX]{x1D706}_{E}}:E\rightarrow E$
is a symmetric endomorphism with respect to the metric
![]() $g_{E}=\unicode[STIX]{x1D6FA}(\cdot ,J_{E}\cdot )$
.
$g_{E}=\unicode[STIX]{x1D6FA}(\cdot ,J_{E}\cdot )$
.
Proof. Let
![]() $q\in Q$
and
$q\in Q$
and
![]() $e_{1}$
,
$e_{1}$
,
![]() $e_{2}\in E_{q}$
. We compute
$e_{2}\in E_{q}$
. We compute
 $$\begin{eqnarray}\displaystyle \langle D^{v}Y_{dg}(q)e_{1},e_{2}\rangle & = & \displaystyle \unicode[STIX]{x1D6FA}(D^{v}Y_{dg}(q)e_{1},J_{E}e_{2})\nonumber\\ \displaystyle d\unicode[STIX]{x1D706}_{E}(D^{v}Y_{dg}(q)e_{1},J_{E}e_{2}) & = & \displaystyle \unicode[STIX]{x1D6FA}\left(\left.\frac{d}{dr}\right|_{r=0}I_{re_{1};q}((Y_{dg})^{v}(re_{1})),J_{E}e_{2}\right)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FA}\left(\left.\frac{d}{dr}\right|_{r=0}I_{re_{1};q}(X_{g}^{\unicode[STIX]{x1D6FA}}(re_{1})),J_{E}e_{2}\right).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \langle D^{v}Y_{dg}(q)e_{1},e_{2}\rangle & = & \displaystyle \unicode[STIX]{x1D6FA}(D^{v}Y_{dg}(q)e_{1},J_{E}e_{2})\nonumber\\ \displaystyle d\unicode[STIX]{x1D706}_{E}(D^{v}Y_{dg}(q)e_{1},J_{E}e_{2}) & = & \displaystyle \unicode[STIX]{x1D6FA}\left(\left.\frac{d}{dr}\right|_{r=0}I_{re_{1};q}((Y_{dg})^{v}(re_{1})),J_{E}e_{2}\right)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FA}\left(\left.\frac{d}{dr}\right|_{r=0}I_{re_{1};q}(X_{g}^{\unicode[STIX]{x1D6FA}}(re_{1})),J_{E}e_{2}\right).\nonumber\end{eqnarray}$$
Here
![]() $d/dr|_{r=0}X_{g}^{\unicode[STIX]{x1D6FA}}(re_{1})$
is nothing but
$d/dr|_{r=0}X_{g}^{\unicode[STIX]{x1D6FA}}(re_{1})$
is nothing but
where
![]() $DX_{g}^{\unicode[STIX]{x1D6FA}}(q)$
is the linearization of the Hamiltonian vector field of
$DX_{g}^{\unicode[STIX]{x1D6FA}}(q)$
is the linearization of the Hamiltonian vector field of
![]() $g|_{E_{q}}$
of the symplectic inner product
$g|_{E_{q}}$
of the symplectic inner product
![]() $\unicode[STIX]{x1D6FA}(q)$
on
$\unicode[STIX]{x1D6FA}(q)$
on
![]() $E_{q}$
. Therefore, it lies at the symplectic Lie algebra
$E_{q}$
. Therefore, it lies at the symplectic Lie algebra
![]() $sp(\unicode[STIX]{x1D6FA})$
and so satisfies
$sp(\unicode[STIX]{x1D6FA})$
and so satisfies
which is equivalent to saying that
![]() $J_{E}DX_{g}^{\unicode[STIX]{x1D6FA}}(q)$
is symmetric with respect to the inner product
$J_{E}DX_{g}^{\unicode[STIX]{x1D6FA}}(q)$
is symmetric with respect to the inner product
![]() $g_{E}=\unicode[STIX]{x1D6FA}(\cdot ,J_{E}\cdot )$
. But we also have
$g_{E}=\unicode[STIX]{x1D6FA}(\cdot ,J_{E}\cdot )$
. But we also have
On the other hand, (7.4) also implies
with
![]() $e_{1}$
replaced by
$e_{1}$
replaced by
![]() $Je_{1}$
therein. The first term becomes
$Je_{1}$
therein. The first term becomes
and the second term can be written as
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FA}(DX_{g}^{\unicode[STIX]{x1D6FA}}(q)(J_{E}e_{2}),e_{1}) & = & \displaystyle -\unicode[STIX]{x1D6FA}(J_{E}e_{2},DX_{g}^{\unicode[STIX]{x1D6FA}}(q)(e_{1}))\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FA}(e_{2},J_{E}DX_{g}^{\unicode[STIX]{x1D6FA}}(q)(e_{1}))\nonumber\\ \displaystyle & = & \displaystyle \langle e_{2},DX_{g}^{\unicode[STIX]{x1D6FA}}(q)(e_{1})\rangle .\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FA}(DX_{g}^{\unicode[STIX]{x1D6FA}}(q)(J_{E}e_{2}),e_{1}) & = & \displaystyle -\unicode[STIX]{x1D6FA}(J_{E}e_{2},DX_{g}^{\unicode[STIX]{x1D6FA}}(q)(e_{1}))\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FA}(e_{2},J_{E}DX_{g}^{\unicode[STIX]{x1D6FA}}(q)(e_{1}))\nonumber\\ \displaystyle & = & \displaystyle \langle e_{2},DX_{g}^{\unicode[STIX]{x1D6FA}}(q)(e_{1})\rangle .\nonumber\end{eqnarray}$$
Combining the two, we have finished the proof. ◻
8
 $CR$
-almost complex structures adapted to
$CR$
-almost complex structures adapted to
 $Q$
$Q$
We would like to emphasize that we have not involved any almost complex structure yet. Now we involve
![]() $J$
in our discussion.
$J$
in our discussion.
Let
![]() $J$
be any
$J$
be any
![]() $CR$
-almost complex structure compatible to
$CR$
-almost complex structure compatible to
![]() $\unicode[STIX]{x1D706}$
in that
$\unicode[STIX]{x1D706}$
in that
![]() $(M,\unicode[STIX]{x1D706},J)$
defines a contact triad and denote by
$(M,\unicode[STIX]{x1D706},J)$
defines a contact triad and denote by
![]() $g$
the triad metric. Then we can realize the normal bundle
$g$
the triad metric. Then we can realize the normal bundle
![]() $N_{Q}M=T_{Q}M/TQ$
as the metric normal bundle
$N_{Q}M=T_{Q}M/TQ$
as the metric normal bundle
We start with the following obvious lemma
Lemma 8.1. Consider the foliation
![]() ${\mathcal{N}}$
of
${\mathcal{N}}$
of
![]() $(Q,\unicode[STIX]{x1D714}_{Q})$
, where
$(Q,\unicode[STIX]{x1D714}_{Q})$
, where
![]() $\unicode[STIX]{x1D714}_{Q}=i_{Q}^{\ast }d\unicode[STIX]{x1D706}$
. Then
$\unicode[STIX]{x1D714}_{Q}=i_{Q}^{\ast }d\unicode[STIX]{x1D706}$
. Then
![]() $JT{\mathcal{N}}$
is perpendicular to
$JT{\mathcal{N}}$
is perpendicular to
![]() $TQ$
with respect to the triad metric of
$TQ$
with respect to the triad metric of
![]() $(M,\unicode[STIX]{x1D706},J)$
. In particular
$(M,\unicode[STIX]{x1D706},J)$
. In particular
![]() $JT{\mathcal{N}}\subset N_{Q}^{g}M$
.
$JT{\mathcal{N}}\subset N_{Q}^{g}M$
.
Proof. The first statement follows from the property that
![]() $T{\mathcal{N}}$
is isotropic with respect to
$T{\mathcal{N}}$
is isotropic with respect to
![]() $\unicode[STIX]{x1D714}_{Q}$
.◻
$\unicode[STIX]{x1D714}_{Q}$
.◻
Now, we introduce the concept of almost complex structures adapted to the locus
![]() $Q$
of closed Reeb orbits of
$Q$
of closed Reeb orbits of
![]() $M$
.
$M$
.
Definition 8.2. Let
![]() $Q\subset M$
be the locus of closed Reeb orbits of Morse–Bott contact form
$Q\subset M$
be the locus of closed Reeb orbits of Morse–Bott contact form
![]() $\unicode[STIX]{x1D706}$
. Suppose
$\unicode[STIX]{x1D706}$
. Suppose
![]() $J$
defines a contact triad
$J$
defines a contact triad
![]() $(M,\unicode[STIX]{x1D706},J)$
. We say a
$(M,\unicode[STIX]{x1D706},J)$
. We say a
![]() $CR$
-almost complex structure
$CR$
-almost complex structure
![]() $J$
for
$J$
for
![]() $(M,\unicode[STIX]{x1D709})$
is adapted to the submanifold
$(M,\unicode[STIX]{x1D709})$
is adapted to the submanifold
![]() $Q$
if
$Q$
if
![]() $J$
satisfies
$J$
satisfies
Proposition 8.3. The set of adapted
![]() $J$
relative to
$J$
relative to
![]() $Q$
is nonempty and is a contractible infinite-dimensional manifold.
$Q$
is nonempty and is a contractible infinite-dimensional manifold.
Proof. For the existence of a
![]() $J$
adapted to
$J$
adapted to
![]() $Q$
, we recall the splitting
$Q$
, we recall the splitting
 $$\begin{eqnarray}\displaystyle T_{q}Q & = & \displaystyle \mathbb{R}\{X_{\unicode[STIX]{x1D706}}(q)\}\oplus T_{q}{\mathcal{N}}\oplus G_{q},\nonumber\\ \displaystyle T_{q}M & \cong & \displaystyle (\mathbb{R}\{X_{\unicode[STIX]{x1D706}}(q)\}\oplus T_{q}{\mathcal{N}}\oplus G_{q})\oplus (T_{q}^{\ast }{\mathcal{N}}\oplus E_{q})\nonumber\\ \displaystyle & = & \displaystyle \mathbb{R}\{X_{\unicode[STIX]{x1D706}}(q)\}\oplus (T_{q}{\mathcal{N}}\oplus T_{q}^{\ast }{\mathcal{N}})\oplus G_{q}\oplus E_{q}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle T_{q}Q & = & \displaystyle \mathbb{R}\{X_{\unicode[STIX]{x1D706}}(q)\}\oplus T_{q}{\mathcal{N}}\oplus G_{q},\nonumber\\ \displaystyle T_{q}M & \cong & \displaystyle (\mathbb{R}\{X_{\unicode[STIX]{x1D706}}(q)\}\oplus T_{q}{\mathcal{N}}\oplus G_{q})\oplus (T_{q}^{\ast }{\mathcal{N}}\oplus E_{q})\nonumber\\ \displaystyle & = & \displaystyle \mathbb{R}\{X_{\unicode[STIX]{x1D706}}(q)\}\oplus (T_{q}{\mathcal{N}}\oplus T_{q}^{\ast }{\mathcal{N}})\oplus G_{q}\oplus E_{q}\nonumber\end{eqnarray}$$
on each connected component of
![]() $Q$
. Therefore, we can find
$Q$
. Therefore, we can find
![]() $J$
so that it is compatible on
$J$
so that it is compatible on
![]() $T{\mathcal{N}}\oplus T^{\ast }{\mathcal{N}}$
with respect to
$T{\mathcal{N}}\oplus T^{\ast }{\mathcal{N}}$
with respect to
![]() $-d\unicode[STIX]{x1D6E9}_{G}|_{T{\mathcal{N}}\oplus T^{\ast }{\mathcal{N}}}$
, and compatible on
$-d\unicode[STIX]{x1D6E9}_{G}|_{T{\mathcal{N}}\oplus T^{\ast }{\mathcal{N}}}$
, and compatible on
![]() $G$
with respect to
$G$
with respect to
![]() $\unicode[STIX]{x1D714}_{Q}$
and on
$\unicode[STIX]{x1D714}_{Q}$
and on
![]() $E$
with respect to
$E$
with respect to
![]() $\unicode[STIX]{x1D6FA}$
. It follows that any such
$\unicode[STIX]{x1D6FA}$
. It follows that any such
![]() $J$
is adapted to
$J$
is adapted to
![]() $Q$
. This proves the first statement.
$Q$
. This proves the first statement.
The proof of the second statement will be postponed until appendix. ◻
We note that each summand
![]() $T_{q}{\mathcal{N}}\oplus T_{q}^{\ast }{\mathcal{N}}$
,
$T_{q}{\mathcal{N}}\oplus T_{q}^{\ast }{\mathcal{N}}$
,
![]() $G_{q}$
and
$G_{q}$
and
![]() $E_{q}$
in the above splitting of
$E_{q}$
in the above splitting of
![]() $T_{Q}M$
is symplectic with respect to
$T_{Q}M$
is symplectic with respect to
![]() $d\unicode[STIX]{x1D706}$
.
$d\unicode[STIX]{x1D706}$
.
We recall the embeddings
![]() $T^{\ast }{\mathcal{N}}$
and
$T^{\ast }{\mathcal{N}}$
and
![]() $E$
into
$E$
into
![]() $N_{Q}M$
and the identification
$N_{Q}M$
and the identification
![]() $N_{Q}M\cong T^{\ast }{\mathcal{N}}\oplus E$
discussed in Section 3.2.
$N_{Q}M\cong T^{\ast }{\mathcal{N}}\oplus E$
discussed in Section 3.2.
Lemma 8.4. For any adapted
![]() $J$
, the identification of the normal bundle
$J$
, the identification of the normal bundle
naturally induces the following identifications:
(1)
 $T^{\ast }{\mathcal{N}}\cong JT{\mathcal{N}}$
;
$T^{\ast }{\mathcal{N}}\cong JT{\mathcal{N}}$
;(2)
 $\text{Image}(E{\hookrightarrow}N_{Q}M)=(TQ)^{d\unicode[STIX]{x1D706}}\cap (JT{\mathcal{N}})^{d\unicode[STIX]{x1D706}}$
.
$\text{Image}(E{\hookrightarrow}N_{Q}M)=(TQ)^{d\unicode[STIX]{x1D706}}\cap (JT{\mathcal{N}})^{d\unicode[STIX]{x1D706}}$
.
Proof. (1) follows by looking at the metric
![]() $\langle \cdot ,\cdot \rangle =d\unicode[STIX]{x1D706}(\cdot ,J\cdot )$
. Now restrict it to
$\langle \cdot ,\cdot \rangle =d\unicode[STIX]{x1D706}(\cdot ,J\cdot )$
. Now restrict it to
![]() $(TQ)^{d\unicode[STIX]{x1D706}}$
, we can identify
$(TQ)^{d\unicode[STIX]{x1D706}}$
, we can identify
![]() $E$
with the complement of
$E$
with the complement of
![]() $T{\mathcal{F}}$
with respect to this metric, which is just
$T{\mathcal{F}}$
with respect to this metric, which is just
![]() $(TQ)^{d\unicode[STIX]{x1D706}}\cap (JT{\mathcal{N}})^{d\unicode[STIX]{x1D706}}$
.◻
$(TQ)^{d\unicode[STIX]{x1D706}}\cap (JT{\mathcal{N}})^{d\unicode[STIX]{x1D706}}$
.◻
Lemma 8.5. For any adapted
![]() $J$
,
$J$
,
![]() $JE\subset E$
in the sense of the identification of
$JE\subset E$
in the sense of the identification of
![]() $E$
with the subbundle of
$E$
with the subbundle of
![]() $T_{Q}M$
given in the above lemma.
$T_{Q}M$
given in the above lemma.
Proof. Take
![]() $v\in (TQ)^{d\unicode[STIX]{x1D706}}\cap (JT{\mathcal{N}})^{d\unicode[STIX]{x1D706}}$
, then for any
$v\in (TQ)^{d\unicode[STIX]{x1D706}}\cap (JT{\mathcal{N}})^{d\unicode[STIX]{x1D706}}$
, then for any
![]() $w\in TQ$
,
$w\in TQ$
,
since
![]() $JTQ\subset TQ+JT{\mathcal{N}}$
. Hence
$JTQ\subset TQ+JT{\mathcal{N}}$
. Hence
![]() $Jv\in (TQ)^{d\unicode[STIX]{x1D706}}$
.
$Jv\in (TQ)^{d\unicode[STIX]{x1D706}}$
.
For any
![]() $w\in T{\mathcal{N}}$
,
$w\in T{\mathcal{N}}$
,
since
![]() $v\in (TQ)^{d\unicode[STIX]{x1D706}}$
and
$v\in (TQ)^{d\unicode[STIX]{x1D706}}$
and
![]() $w\in TQ$
. Hence
$w\in TQ$
. Hence
![]() $Jv\in (JT{\mathcal{N}})^{d\unicode[STIX]{x1D706}}$
, and we are done.◻
$Jv\in (JT{\mathcal{N}})^{d\unicode[STIX]{x1D706}}$
, and we are done.◻
Remark 8.6.
(1) We would like to mention that in the nondegenerate case the adaptedness is automatically satisfied by any compatible
 $CR$
-almost complex structure
$CR$
-almost complex structure
 $J\in {\mathcal{J}}(M,\unicode[STIX]{x1D706})$
, because in that case
$J\in {\mathcal{J}}(M,\unicode[STIX]{x1D706})$
, because in that case
 $P$
is a point and
$P$
is a point and
 $HTF=\mathbb{R}\cdot \{X_{F}\}$
and
$HTF=\mathbb{R}\cdot \{X_{F}\}$
and
 $VTF=TF=\unicode[STIX]{x1D709}_{F}$
.
$VTF=TF=\unicode[STIX]{x1D709}_{F}$
.(2) However, for the general Morse–Bott case, the set of adapted
 $CR$
-almost complex structure is strictly smaller than
$CR$
-almost complex structure is strictly smaller than
 ${\mathcal{J}}(M,\unicode[STIX]{x1D706})$
. It appears that for the proof of exponential convergence result of closed Reeb orbits in the Morse–Bott case, this additional restriction of
${\mathcal{J}}(M,\unicode[STIX]{x1D706})$
. It appears that for the proof of exponential convergence result of closed Reeb orbits in the Morse–Bott case, this additional restriction of
 $J$
to those adapted to the Morse–Bott submanifold of closed Reeb orbits in the above sense facilitates geometric computation considerably. (Compare our computations with those given in [Reference BourgeoisBou], [Reference Bourgeois, Eliashberg, Hofer, Wysocki and ZehnderBEHWZ].)
$J$
to those adapted to the Morse–Bott submanifold of closed Reeb orbits in the above sense facilitates geometric computation considerably. (Compare our computations with those given in [Reference BourgeoisBou], [Reference Bourgeois, Eliashberg, Hofer, Wysocki and ZehnderBEHWZ].)(3) When
 $T{\mathcal{N}}=\{0\}$
,
$T{\mathcal{N}}=\{0\}$
,
 $(Q,\unicode[STIX]{x1D706}_{Q})$
carries the structure of prequantization
$(Q,\unicode[STIX]{x1D706}_{Q})$
carries the structure of prequantization
 $Q\rightarrow P=Q/S^{1}$
.
$Q\rightarrow P=Q/S^{1}$
.
We specialize to the normal form
![]() $(U_{F},f\unicode[STIX]{x1D706}_{F})$
. We note that the complex structure
$(U_{F},f\unicode[STIX]{x1D706}_{F})$
. We note that the complex structure
![]() $J_{F}:\unicode[STIX]{x1D709}_{F}\rightarrow \unicode[STIX]{x1D709}_{F}$
canonically induces one on the vector bundle
$J_{F}:\unicode[STIX]{x1D709}_{F}\rightarrow \unicode[STIX]{x1D709}_{F}$
canonically induces one on the vector bundle
![]() $VTF\rightarrow F$
$VTF\rightarrow F$
satisfying
![]() $(J_{F}^{v})^{2}=-\operatorname{id}_{VTF}$
. For any given
$(J_{F}^{v})^{2}=-\operatorname{id}_{VTF}$
. For any given
![]() $J$
adapted to
$J$
adapted to
![]() $o_{F}\subset F$
, it has the decomposition
$o_{F}\subset F$
, it has the decomposition
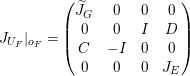 $$\begin{eqnarray}J_{U_{F}}|_{o_{F}}=\left(\begin{array}{@{}cccc@{}}\widetilde{J}_{G} & 0 & 0 & 0\\ 0 & 0 & I & D\\ C & -I & 0 & 0\\ 0 & 0 & 0 & J_{E}\end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}J_{U_{F}}|_{o_{F}}=\left(\begin{array}{@{}cccc@{}}\widetilde{J}_{G} & 0 & 0 & 0\\ 0 & 0 & I & D\\ C & -I & 0 & 0\\ 0 & 0 & 0 & J_{E}\end{array}\right)\end{eqnarray}$$
on the zero section with respect to the splitting
Here we note that
![]() $C\in \operatorname{Hom}(G,T^{\ast }{\mathcal{N}})$
and
$C\in \operatorname{Hom}(G,T^{\ast }{\mathcal{N}})$
and
![]() $D\in \operatorname{Hom}(E,T{\mathcal{N}})$
, which depend on
$D\in \operatorname{Hom}(E,T{\mathcal{N}})$
, which depend on
![]() $J$
. Indeed it is easy to see
$J$
. Indeed it is easy to see
![]() $C=0=D$
from a consideration of the equation
$C=0=D$
from a consideration of the equation
![]() $J_{U}^{2}=-\operatorname{Id}$
.
$J_{U}^{2}=-\operatorname{Id}$
.
Using the splitting
on
![]() $o_{F}\cong Q$
, we lift
$o_{F}\cong Q$
, we lift
![]() $J_{F}$
to a
$J_{F}$
to a
![]() $\unicode[STIX]{x1D706}_{F}$
-compatible almost complex structure on the total space
$\unicode[STIX]{x1D706}_{F}$
-compatible almost complex structure on the total space
![]() $F$
, which we denote by
$F$
, which we denote by
![]() $J_{0}$
. We note that the triad
$J_{0}$
. We note that the triad
![]() $(F,\unicode[STIX]{x1D706}_{F},J_{0})$
is naturally
$(F,\unicode[STIX]{x1D706}_{F},J_{0})$
is naturally
![]() $S^{1}$
-equivariant by the
$S^{1}$
-equivariant by the
![]() $S^{1}$
-action induced by the Reeb flow on
$S^{1}$
-action induced by the Reeb flow on
![]() $Q$
.
$Q$
.
Definition 8.7. (Normalized contact triad
 $(F,\unicode[STIX]{x1D706}_{F},J_{0})$
)
$(F,\unicode[STIX]{x1D706}_{F},J_{0})$
)
We call the
![]() $S^{1}$
-invariant contact triad
$S^{1}$
-invariant contact triad
![]() $(F,\unicode[STIX]{x1D706}_{F},J_{0})$
the normalized contact triad adapted to
$(F,\unicode[STIX]{x1D706}_{F},J_{0})$
the normalized contact triad adapted to
![]() $Q$
.
$Q$
.
Now we are ready to give the proof of the following.
Proposition 8.8. Consider the contact triad
![]() $(U_{F},\unicode[STIX]{x1D706}_{F},J_{0})$
for an adapted
$(U_{F},\unicode[STIX]{x1D706}_{F},J_{0})$
for an adapted
![]() $J$
and its associated triad connection. Then the zero section
$J$
and its associated triad connection. Then the zero section
![]() $o_{F}\cong Q$
is totally geodesic and so naturally induces an affine connection on
$o_{F}\cong Q$
is totally geodesic and so naturally induces an affine connection on
![]() $Q$
. Furthermore, the induced connection on
$Q$
. Furthermore, the induced connection on
![]() $Q$
preserves
$Q$
preserves
![]() $T{\mathcal{F}}$
and the splitting
$T{\mathcal{F}}$
and the splitting
Proof. We note that
![]() $\unicode[STIX]{x1D706}_{F}$
is invariant under the reflection of the vector bundle
$\unicode[STIX]{x1D706}_{F}$
is invariant under the reflection of the vector bundle
![]() $F\rightarrow Q$
by definition (4.8) of
$F\rightarrow Q$
by definition (4.8) of
![]() $\unicode[STIX]{x1D706}_{F}$
and so is
$\unicode[STIX]{x1D706}_{F}$
and so is
![]() $J_{0}$
by the construction given above. Therefore, the triad metric of
$J_{0}$
by the construction given above. Therefore, the triad metric of
![]() $(U_{F},\unicode[STIX]{x1D706}_{F},J_{0})$
is invariant under the reflection. This implies that the associated triad connection, which preserves the triad metric by one of the definition properties [Reference Oh and WangOW1], makes the zero section totally geodesic since it is the fixed point set of the reflection which is an isometry with respect to the triad metric. Therefore, it canonically restricts to an affine connection on
$(U_{F},\unicode[STIX]{x1D706}_{F},J_{0})$
is invariant under the reflection. This implies that the associated triad connection, which preserves the triad metric by one of the definition properties [Reference Oh and WangOW1], makes the zero section totally geodesic since it is the fixed point set of the reflection which is an isometry with respect to the triad metric. Therefore, it canonically restricts to an affine connection on
![]() $o_{F}\cong Q$
.
$o_{F}\cong Q$
.
It remains to show that this connection preserves the splitting
![]() $T{\mathcal{F}}=\mathbb{R}\{X_{\unicode[STIX]{x1D706},Q}\}\oplus T{\mathcal{N}}$
. For the simplicity of notation, we denote
$T{\mathcal{F}}=\mathbb{R}\{X_{\unicode[STIX]{x1D706},Q}\}\oplus T{\mathcal{N}}$
. For the simplicity of notation, we denote
![]() $\unicode[STIX]{x1D706}_{F}=\unicode[STIX]{x1D706}$
in the rest of this proof.
$\unicode[STIX]{x1D706}_{F}=\unicode[STIX]{x1D706}$
in the rest of this proof.
Let
![]() $q\in Q$
and
$q\in Q$
and
![]() $v\in T_{q}Q$
. We pick a vector field
$v\in T_{q}Q$
. We pick a vector field
![]() $Z$
that is tangent to
$Z$
that is tangent to
![]() $Q$
and
$Q$
and
![]() $S^{1}$
-invariant and satisfies
$S^{1}$
-invariant and satisfies
![]() $Z(q)=v$
. Such a vector field exists because
$Z(q)=v$
. Such a vector field exists because
![]() ${\mathcal{F}}$
is the null foliation of
${\mathcal{F}}$
is the null foliation of
![]() $\unicode[STIX]{x1D714}_{Q}=i_{Q}^{\ast }d\unicode[STIX]{x1D706}$
, and
$\unicode[STIX]{x1D714}_{Q}=i_{Q}^{\ast }d\unicode[STIX]{x1D706}$
, and
![]() $Q$
carries the
$Q$
carries the
![]() $S^{1}$
-action induced by the Reeb flow of
$S^{1}$
-action induced by the Reeb flow of
![]() $\unicode[STIX]{x1D706}$
. If
$\unicode[STIX]{x1D706}$
. If
![]() $Z$
is a multiple of
$Z$
is a multiple of
![]() $X_{\unicode[STIX]{x1D706}}$
, then we can choose
$X_{\unicode[STIX]{x1D706}}$
, then we can choose
![]() $Z=c\,X_{\unicode[STIX]{x1D706}}$
for some constant and so
$Z=c\,X_{\unicode[STIX]{x1D706}}$
for some constant and so
![]() $\unicode[STIX]{x1D6FB}_{Z}X_{\unicode[STIX]{x1D706}}=0$
by the axiom
$\unicode[STIX]{x1D6FB}_{Z}X_{\unicode[STIX]{x1D706}}=0$
by the axiom
![]() $\unicode[STIX]{x1D6FB}_{X_{\unicode[STIX]{x1D706}}}X_{\unicode[STIX]{x1D706}}=0$
of contact triad connection. Then for
$\unicode[STIX]{x1D6FB}_{X_{\unicode[STIX]{x1D706}}}X_{\unicode[STIX]{x1D706}}=0$
of contact triad connection. Then for
![]() $Y\in \unicode[STIX]{x1D709}\cap T{\mathcal{F}}$
, we compute
$Y\in \unicode[STIX]{x1D709}\cap T{\mathcal{F}}$
, we compute
by an axiom of the triad connection. On the other hand, for any
![]() $Z$
tangent to
$Z$
tangent to
![]() $Q$
, we derive
$Q$
, we derive
since
![]() $Q=o_{F}$
is totally geodesic and so
$Q=o_{F}$
is totally geodesic and so
![]() $\unicode[STIX]{x1D6FB}_{X_{\unicode[STIX]{x1D706}}}Z\in TQ$
. This proves that
$\unicode[STIX]{x1D6FB}_{X_{\unicode[STIX]{x1D706}}}Z\in TQ$
. This proves that
![]() $\unicode[STIX]{x1D6FB}_{X_{\unicode[STIX]{x1D706}}}T{\mathcal{N}}\subset T{\mathcal{N}}$
.
$\unicode[STIX]{x1D6FB}_{X_{\unicode[STIX]{x1D706}}}T{\mathcal{N}}\subset T{\mathcal{N}}$
.
For
![]() $v\in T_{q}Q\cap \unicode[STIX]{x1D709}_{q}$
, we have
$v\in T_{q}Q\cap \unicode[STIX]{x1D709}_{q}$
, we have
![]() $\unicode[STIX]{x1D6FB}_{Z}X_{\unicode[STIX]{x1D706}}\in \unicode[STIX]{x1D709}\cap TQ$
. On the other hand,
$\unicode[STIX]{x1D6FB}_{Z}X_{\unicode[STIX]{x1D706}}\in \unicode[STIX]{x1D709}\cap TQ$
. On the other hand,
since
![]() $[Z,X_{\unicode[STIX]{x1D706}}]=0$
by the
$[Z,X_{\unicode[STIX]{x1D706}}]=0$
by the
![]() $S^{1}$
-invariance of
$S^{1}$
-invariance of
![]() $Z$
. Now let
$Z$
. Now let
![]() $W\in T{\mathcal{N}}$
and compute
$W\in T{\mathcal{N}}$
and compute
On the other hand
![]() $J_{0}W\in T^{\ast }{\mathcal{N}}\subset T_{o_{F}}F$
since
$J_{0}W\in T^{\ast }{\mathcal{N}}\subset T_{o_{F}}F$
since
![]() ${\mathcal{F}}$
is (maximally) isotropic with respect to
${\mathcal{F}}$
is (maximally) isotropic with respect to
![]() $d\unicode[STIX]{x1D706}$
. Therefore, we obtain
$d\unicode[STIX]{x1D706}$
. Therefore, we obtain
This proves
![]() $\unicode[STIX]{x1D6FB}_{Z}X_{\unicode[STIX]{x1D706}}$
is perpendicular to
$\unicode[STIX]{x1D6FB}_{Z}X_{\unicode[STIX]{x1D706}}$
is perpendicular to
![]() $T{\mathcal{N}}$
with respect to the triad metric and so must be parallel to
$T{\mathcal{N}}$
with respect to the triad metric and so must be parallel to
![]() $X_{\unicode[STIX]{x1D706}}$
. On the other hand,
$X_{\unicode[STIX]{x1D706}}$
. On the other hand,
and hence if
![]() $W\in T{\mathcal{N}}$
, it must be perpendicular to
$W\in T{\mathcal{N}}$
, it must be perpendicular to
![]() $X_{\unicode[STIX]{x1D706}}$
. Furthermore, we have
$X_{\unicode[STIX]{x1D706}}$
. Furthermore, we have
for any
![]() $V$
tangent to
$V$
tangent to
![]() $Q$
since
$Q$
since
![]() $\unicode[STIX]{x1D6FB}_{Z}V\in TQ$
as
$\unicode[STIX]{x1D6FB}_{Z}V\in TQ$
as
![]() $Q$
is totally geodesic. This proves
$Q$
is totally geodesic. This proves
![]() $\unicode[STIX]{x1D6FB}_{Z}W$
indeed lies in
$\unicode[STIX]{x1D6FB}_{Z}W$
indeed lies in
![]() $\unicode[STIX]{x1D709}\cap T{\mathcal{F}}=T{\mathcal{N}}$
, which finishes the proof.◻
$\unicode[STIX]{x1D709}\cap T{\mathcal{F}}=T{\mathcal{N}}$
, which finishes the proof.◻
Part 2 Exponential estimates for contact instantons: Morse–Bott case
In this part, we develop the three-interval method of proving
![]() $C^{\infty }$
exponential convergence to closed Reeb orbits of any (charge vanishing) contact instanton with finite
$C^{\infty }$
exponential convergence to closed Reeb orbits of any (charge vanishing) contact instanton with finite
![]() $\unicode[STIX]{x1D70B}$
-energy and bounded gradient of any Morse–Bott contact form, and use it at each puncture of domain Riemann surface.
$\unicode[STIX]{x1D70B}$
-energy and bounded gradient of any Morse–Bott contact form, and use it at each puncture of domain Riemann surface.
The contents of this part are as follows:
∙ in Section 9, we briefly review the subsequence convergence result for contact instantons with finite
 $\unicode[STIX]{x1D70B}$
-energy and bounded gradient. This is the starting point for applying the three-interval method introduced in Section 10 and afterward;
$\unicode[STIX]{x1D70B}$
-energy and bounded gradient. This is the starting point for applying the three-interval method introduced in Section 10 and afterward;∙ in Section 10, an abstract three-interval method framework is presented;
∙ in Section 11, we focus on the prequantization case and use the three-interval machinery introduced in Section 10 to prove exponential convergence. The proof is divided into several steps which are organized into different subsections;
∙ in Section 12, we prove exponential decay for general cases;
∙ in Section 13, we explain how to apply this method to symplectic manifolds with asymptotically cylindrical ends.
9 Subsequence convergence on the adapted contact triad
 $(U_{F},\unicode[STIX]{x1D706},J)$
$(U_{F},\unicode[STIX]{x1D706},J)$
We first introduce the subsequence convergence result for Morse–Bott contact instantons of finite
![]() $\unicode[STIX]{x1D70B}$
-energy and finite gradient bound. The proofs are almost word by word the same as the nondegenerate case considered in [Reference Oh and WangOW2]. For readers’ convenience, we include details here.
$\unicode[STIX]{x1D70B}$
-energy and finite gradient bound. The proofs are almost word by word the same as the nondegenerate case considered in [Reference Oh and WangOW2]. For readers’ convenience, we include details here.
We fix a punctured Riemann surface
![]() $(\dot{\unicode[STIX]{x1D6F4}},j)$
with
$(\dot{\unicode[STIX]{x1D6F4}},j)$
with
![]() $l$
-punctures and associate it with a metric
$l$
-punctures and associate it with a metric
![]() $h$
which is cylindrical at each end. To be precise, it means that there exists a compact set
$h$
which is cylindrical at each end. To be precise, it means that there exists a compact set
![]() $K_{\unicode[STIX]{x1D6F4}}\subset \dot{\unicode[STIX]{x1D6F4}}$
, such that
$K_{\unicode[STIX]{x1D6F4}}\subset \dot{\unicode[STIX]{x1D6F4}}$
, such that
![]() $\dot{\unicode[STIX]{x1D6F4}}-\text{Int}(K_{\unicode[STIX]{x1D6F4}})$
is the disjoint union of
$\dot{\unicode[STIX]{x1D6F4}}-\text{Int}(K_{\unicode[STIX]{x1D6F4}})$
is the disjoint union of
![]() $l^{+}$
-positive half cylinders and
$l^{+}$
-positive half cylinders and
![]() $l^{-}$
-negative half cylinders with
$l^{-}$
-negative half cylinders with
![]() $l=l^{+}+l^{-}$
, that is
$l=l^{+}+l^{-}$
, that is
 $$\begin{eqnarray}\dot{\unicode[STIX]{x1D6F4}}-\text{Int}(K_{\unicode[STIX]{x1D6F4}})=\left(\mathop{\bigsqcup }_{i=1,\ldots ,l^{+}}C_{i}^{+}\right)\sqcup \left(\mathop{\bigsqcup }_{i=1,\ldots ,l^{-}}C_{i}^{-}\right),\quad l=l^{+}+l^{-}\end{eqnarray}$$
$$\begin{eqnarray}\dot{\unicode[STIX]{x1D6F4}}-\text{Int}(K_{\unicode[STIX]{x1D6F4}})=\left(\mathop{\bigsqcup }_{i=1,\ldots ,l^{+}}C_{i}^{+}\right)\sqcup \left(\mathop{\bigsqcup }_{i=1,\ldots ,l^{-}}C_{i}^{-}\right),\quad l=l^{+}+l^{-}\end{eqnarray}$$
where
equipped with the cylindrical metric
![]() $h|_{C_{i}^{\pm }}=d\unicode[STIX]{x1D70F}^{2}+dt^{2}$
thereon. For any smooth map
$h|_{C_{i}^{\pm }}=d\unicode[STIX]{x1D70F}^{2}+dt^{2}$
thereon. For any smooth map
![]() $w:\dot{\unicode[STIX]{x1D6F4}}\rightarrow M$
, the
$w:\dot{\unicode[STIX]{x1D6F4}}\rightarrow M$
, the
![]() $\unicode[STIX]{x1D70B}$
-harmonic energy
$\unicode[STIX]{x1D70B}$
-harmonic energy
![]() $E^{\unicode[STIX]{x1D70B}}(w)$
is defined as
$E^{\unicode[STIX]{x1D70B}}(w)$
is defined as
where the norm is taken by
![]() $h$
and the triad metric on
$h$
and the triad metric on
![]() $M$
.
$M$
.
We put the following hypotheses on the asymptotic study of Morse–Bott contact instantons:
Hypothesis 9.1. Consider the contact triad
![]() $(M,\unicode[STIX]{x1D706},J)$
with Morse–Bott contact form
$(M,\unicode[STIX]{x1D706},J)$
with Morse–Bott contact form
![]() $\unicode[STIX]{x1D706}$
. Let
$\unicode[STIX]{x1D706}$
. Let
![]() $w:\dot{\unicode[STIX]{x1D6F4}}\rightarrow M$
be a contact instanton, that is, satisfy the contact-instanton equations (1.1) defined on a punctured Riemann surface with cylindrical ends
$w:\dot{\unicode[STIX]{x1D6F4}}\rightarrow M$
be a contact instanton, that is, satisfy the contact-instanton equations (1.1) defined on a punctured Riemann surface with cylindrical ends
![]() $(\dot{\unicode[STIX]{x1D6F4}},j,h)$
. We assume that
$(\dot{\unicode[STIX]{x1D6F4}},j,h)$
. We assume that
![]() $w$
satisfies
$w$
satisfies
(1)
 $E^{\unicode[STIX]{x1D70B}}(w):=E_{(\unicode[STIX]{x1D706},J;\dot{\unicode[STIX]{x1D6F4}},h)}^{\unicode[STIX]{x1D70B}}(w)<\infty$
, that is, finite
$E^{\unicode[STIX]{x1D70B}}(w):=E_{(\unicode[STIX]{x1D706},J;\dot{\unicode[STIX]{x1D6F4}},h)}^{\unicode[STIX]{x1D70B}}(w)<\infty$
, that is, finite
 $\unicode[STIX]{x1D70B}$
-energy;
$\unicode[STIX]{x1D70B}$
-energy;(2)
 $\Vert dw\Vert _{L^{\infty }(\dot{\unicode[STIX]{x1D6F4}})}<\infty$
, that is, finite gradient bound.
$\Vert dw\Vert _{L^{\infty }(\dot{\unicode[STIX]{x1D6F4}})}<\infty$
, that is, finite gradient bound.
The following two asymptotic invariants associated to each puncture play essential roles in the study of asymptotic behavior of a Morse–Bott contact instanton satisfying Hypothesis 9.1.
Definition 9.2. Let
![]() $w:\dot{\unicode[STIX]{x1D6F4}}\rightarrow M$
be as in Hypothesis 9.1. At each puncture, we define the asymptotic contact action
$w:\dot{\unicode[STIX]{x1D6F4}}\rightarrow M$
be as in Hypothesis 9.1. At each puncture, we define the asymptotic contact action
![]() ${\mathcal{T}}_{C_{i}^{\pm }}(w)$
and the asymptotic contact charge
${\mathcal{T}}_{C_{i}^{\pm }}(w)$
and the asymptotic contact charge
![]() ${\mathcal{Q}}_{C_{i}^{\pm }}(w)$
for a contact instanton
${\mathcal{Q}}_{C_{i}^{\pm }}(w)$
for a contact instanton
![]() $w$
satisfying Hypothesis 9.1 as
$w$
satisfying Hypothesis 9.1 as
where
![]() $C^{\pm }$
is the cylindrical end associated to the given puncture.
$C^{\pm }$
is the cylindrical end associated to the given puncture.
The following remark shows that both
![]() ${\mathcal{T}}$
and
${\mathcal{T}}$
and
![]() ${\mathcal{Q}}$
are translation invariant.
${\mathcal{Q}}$
are translation invariant.
Remark 9.3. For any contact instanton
![]() $w$
satisfying Hypothesis 9.1 at a puncture
$w$
satisfying Hypothesis 9.1 at a puncture
![]() $[0,\infty )\times S^{1}$
, we have
$[0,\infty )\times S^{1}$
, we have
which is due to
![]() $(1/2)|d^{\unicode[STIX]{x1D70B}}w|^{2}\,dA=d(w^{\ast }\unicode[STIX]{x1D706})$
and Stokes’ formula; and
$(1/2)|d^{\unicode[STIX]{x1D70B}}w|^{2}\,dA=d(w^{\ast }\unicode[STIX]{x1D706})$
and Stokes’ formula; and
which is due to
![]() $d(w^{\ast }\unicode[STIX]{x1D706}\circ j)=0$
.
$d(w^{\ast }\unicode[STIX]{x1D706}\circ j)=0$
.
Since our main interest lies on the asymptotic behavior of a fixed contact instanton
![]() $w$
at a given puncture, we assume the domain of
$w$
at a given puncture, we assume the domain of
![]() $w$
is a positive half cylinder
$w$
is a positive half cylinder
![]() $[0,\infty )\times S^{1}$
without loss of generality. (The case of negative half cylinder can be treated in the same way.) We simply denote the asymptotic contact action and charge at this puncture by
$[0,\infty )\times S^{1}$
without loss of generality. (The case of negative half cylinder can be treated in the same way.) We simply denote the asymptotic contact action and charge at this puncture by
![]() ${\mathcal{T}}$
and by
${\mathcal{T}}$
and by
![]() ${\mathcal{Q}}$
, respectively.
${\mathcal{Q}}$
, respectively.
Theorem 9.4. (Subsequence convergence [Reference Oh and WangOW2])
Let
![]() $(M,\unicode[STIX]{x1D706},J)$
be any, not necessarily Morse–Bott, contact triad. Assume
$(M,\unicode[STIX]{x1D706},J)$
be any, not necessarily Morse–Bott, contact triad. Assume
![]() $w:[0,\infty )\times S^{1}\rightarrow M$
is a contact instanton, that is it satisfies the contact-instanton equations (1.1), and satisfies Hypothesis 9.1. Then for any sequence
$w:[0,\infty )\times S^{1}\rightarrow M$
is a contact instanton, that is it satisfies the contact-instanton equations (1.1), and satisfies Hypothesis 9.1. Then for any sequence
![]() $s_{k}\rightarrow \infty$
, there exists a subsequence, still denoted by
$s_{k}\rightarrow \infty$
, there exists a subsequence, still denoted by
![]() $s_{k}$
, and a Reeb trajectory
$s_{k}$
, and a Reeb trajectory
![]() $\unicode[STIX]{x1D6FE}$
, not necessarily closed, such that
$\unicode[STIX]{x1D6FE}$
, not necessarily closed, such that
in the
![]() $C^{l}(K\times S^{1},M)$
sense for any
$C^{l}(K\times S^{1},M)$
sense for any
![]() $l\geqslant 0$
, where
$l\geqslant 0$
, where
![]() $K\subset \mathbb{R}$
is an arbitrary compact set.
$K\subset \mathbb{R}$
is an arbitrary compact set.
Furthermore, when
![]() $(M,\unicode[STIX]{x1D706},J)$
is of Morse–Bott type and
$(M,\unicode[STIX]{x1D706},J)$
is of Morse–Bott type and
![]() $w$
has nonvanishing period
$w$
has nonvanishing period
![]() ${\mathcal{T}}\neq 0$
, then there exists a connected submanifold
${\mathcal{T}}\neq 0$
, then there exists a connected submanifold
![]() $Q$
foliated by closed Reeb orbits of period
$Q$
foliated by closed Reeb orbits of period
![]() ${\mathcal{T}}$
, so that the limit becomes
${\mathcal{T}}$
, so that the limit becomes
![]() $\unicode[STIX]{x1D6FE}(-{\mathcal{Q}}\unicode[STIX]{x1D70F}+{\mathcal{T}}\,t)$
, where
$\unicode[STIX]{x1D6FE}(-{\mathcal{Q}}\unicode[STIX]{x1D70F}+{\mathcal{T}}\,t)$
, where
![]() $z$
is a closed Reeb orbit over
$z$
is a closed Reeb orbit over
![]() $Q$
.
$Q$
.
The first part of the theorem was proved in [Reference Oh and WangOW2, Section 6]. For reader’s convenience, we include its complete proof in Appendix B. Similar statement for Morse–Bott case in the context of symplectization was proved in [Reference Hofer, Wysocki and ZehnderHWZ3, Proposition 2.1] (see also [Reference Hofer, Wysocki and ZehnderHWZ1, Reference Hofer, Wysocki and ZehnderHWZ2, Proposition 2.1]).
Corollary 9.5. Assume
![]() $w:[0,\infty )\times S^{1}\rightarrow M$
is a contact instanton, that is it satisfies the contact-instanton equations (1.1) in a Morse–Bott contact triad
$w:[0,\infty )\times S^{1}\rightarrow M$
is a contact instanton, that is it satisfies the contact-instanton equations (1.1) in a Morse–Bott contact triad
![]() $(M,\unicode[STIX]{x1D706},J)$
, and satisfies Hypothesis 9.1. Then
$(M,\unicode[STIX]{x1D706},J)$
, and satisfies Hypothesis 9.1. Then
 $$\begin{eqnarray}\displaystyle & & \displaystyle \lim _{s\rightarrow \infty }\left|\unicode[STIX]{x1D70B}\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}(s+\unicode[STIX]{x1D70F},t)\right|=0,\qquad \lim _{s\rightarrow \infty }\left|\unicode[STIX]{x1D70B}\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}t}(s+\unicode[STIX]{x1D70F},t)\right|=0\nonumber\\ \displaystyle & & \displaystyle \lim _{s\rightarrow \infty }\unicode[STIX]{x1D706}\left(\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}\right)(s+\unicode[STIX]{x1D70F},t)=-{\mathcal{Q}},\qquad \lim _{s\rightarrow \infty }\unicode[STIX]{x1D706}\left(\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}t}\right)(s+\unicode[STIX]{x1D70F},t)={\mathcal{T}}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \lim _{s\rightarrow \infty }\left|\unicode[STIX]{x1D70B}\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}(s+\unicode[STIX]{x1D70F},t)\right|=0,\qquad \lim _{s\rightarrow \infty }\left|\unicode[STIX]{x1D70B}\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}t}(s+\unicode[STIX]{x1D70F},t)\right|=0\nonumber\\ \displaystyle & & \displaystyle \lim _{s\rightarrow \infty }\unicode[STIX]{x1D706}\left(\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}\right)(s+\unicode[STIX]{x1D70F},t)=-{\mathcal{Q}},\qquad \lim _{s\rightarrow \infty }\unicode[STIX]{x1D706}\left(\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}t}\right)(s+\unicode[STIX]{x1D70F},t)={\mathcal{T}}\nonumber\end{eqnarray}$$
and
All the limits are uniform for
![]() $(\unicode[STIX]{x1D70F},t)$
in
$(\unicode[STIX]{x1D70F},t)$
in
![]() $K\times S^{1}$
with compact
$K\times S^{1}$
with compact
![]() $K\subset \mathbb{R}$
.
$K\subset \mathbb{R}$
.
From now on, we consider
![]() $J$
as a
$J$
as a
![]() $CR$
-almost complex structure adapted to
$CR$
-almost complex structure adapted to
![]() $Q$
, which in turn induces a
$Q$
, which in turn induces a
![]() $CR$
-almost complex structure on a neighborhood
$CR$
-almost complex structure on a neighborhood
![]() $U_{F}$
of the zero section of
$U_{F}$
of the zero section of
![]() $F$
. Denote by
$F$
. Denote by
![]() $(U_{F},\unicode[STIX]{x1D706},J)$
the corresponding adapted contact triad.
$(U_{F},\unicode[STIX]{x1D706},J)$
the corresponding adapted contact triad.
When restricted to each connected component of the loci of closed Reeb orbits, there exists a uniform constant
![]() $\unicode[STIX]{x1D70F}_{0}>0$
such that the image of
$\unicode[STIX]{x1D70F}_{0}>0$
such that the image of
![]() $w$
lies in a tubular neighborhood of
$w$
lies in a tubular neighborhood of
![]() $Q$
whenever
$Q$
whenever
![]() $\unicode[STIX]{x1D70F}>\unicode[STIX]{x1D70F}_{0}$
. In other words, it is enough to restrict ourselves to study contact-instanton maps from half cylinder
$\unicode[STIX]{x1D70F}>\unicode[STIX]{x1D70F}_{0}$
. In other words, it is enough to restrict ourselves to study contact-instanton maps from half cylinder
![]() $[0,\infty )\times S^{1}$
to the canonical neighborhood
$[0,\infty )\times S^{1}$
to the canonical neighborhood
![]() $(U_{F},\unicode[STIX]{x1D706},J)$
defined in Definition 5.4 for the purpose of the study of asymptotic behavior at the end.
$(U_{F},\unicode[STIX]{x1D706},J)$
defined in Definition 5.4 for the purpose of the study of asymptotic behavior at the end.
With the normal form we developed in Part 1, we express
![]() $w$
as
$w$
as
![]() $w=(u,s)$
where
$w=(u,s)$
where
![]() $u:=\unicode[STIX]{x1D70B}\circ w:[0,\infty )\times S^{1}\rightarrow Q$
and
$u:=\unicode[STIX]{x1D70B}\circ w:[0,\infty )\times S^{1}\rightarrow Q$
and
![]() $s=(\unicode[STIX]{x1D707},e)$
is a section of the pullback bundle
$s=(\unicode[STIX]{x1D707},e)$
is a section of the pullback bundle
![]() $u^{\ast }(JT{\mathcal{N}})\oplus u^{\ast }E\rightarrow [0,\infty )\times S^{1}$
. Recall from Section 7 and express
$u^{\ast }(JT{\mathcal{N}})\oplus u^{\ast }E\rightarrow [0,\infty )\times S^{1}$
. Recall from Section 7 and express
 $$\begin{eqnarray}dw=\left(\begin{array}{@{}c@{}}du\\ \unicode[STIX]{x1D6FB}_{du}s\end{array}\right)=\left(\begin{array}{@{}c@{}}du\\ \unicode[STIX]{x1D6FB}_{du}\unicode[STIX]{x1D707}\\ \unicode[STIX]{x1D6FB}_{du}e\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}dw=\left(\begin{array}{@{}c@{}}du\\ \unicode[STIX]{x1D6FB}_{du}s\end{array}\right)=\left(\begin{array}{@{}c@{}}du\\ \unicode[STIX]{x1D6FB}_{du}\unicode[STIX]{x1D707}\\ \unicode[STIX]{x1D6FB}_{du}e\end{array}\right),\end{eqnarray}$$
we reinterpret the convergence of
![]() $w$
stated in Theorem 9.4 in terms of the coordinate
$w$
stated in Theorem 9.4 in terms of the coordinate
![]() $w=(u,s)=(u,(\unicode[STIX]{x1D707},e))$
.
$w=(u,s)=(u,(\unicode[STIX]{x1D707},e))$
.
Corollary 9.6. Let
![]() $w=(u,s)=(u,(\unicode[STIX]{x1D707},e))$
satisfy the same assumption as in Theorem 9.4. Then for any sequence
$w=(u,s)=(u,(\unicode[STIX]{x1D707},e))$
satisfy the same assumption as in Theorem 9.4. Then for any sequence
![]() $s_{k}\rightarrow \infty$
, there exists a subsequence, still denoted by
$s_{k}\rightarrow \infty$
, there exists a subsequence, still denoted by
![]() $s_{k}$
, and a Reeb orbit
$s_{k}$
, and a Reeb orbit
![]() $\unicode[STIX]{x1D6FE}$
on
$\unicode[STIX]{x1D6FE}$
on
![]() $Q$
(may depend on the choice of subsequences) with action
$Q$
(may depend on the choice of subsequences) with action
![]() ${\mathcal{T}}$
and charge
${\mathcal{T}}$
and charge
![]() ${\mathcal{Q}}$
, such that
${\mathcal{Q}}$
, such that
in
![]() $C^{l}(K\times S^{1},M)$
sense for any
$C^{l}(K\times S^{1},M)$
sense for any
![]() $l$
, where
$l$
, where
![]() $K\subset [0,\infty )$
is an arbitrary compact set. Furthermore, we have
$K\subset [0,\infty )$
is an arbitrary compact set. Furthermore, we have
 $$\begin{eqnarray}\displaystyle \displaystyle \lim _{s\rightarrow \infty }|\unicode[STIX]{x1D707}(s+\unicode[STIX]{x1D70F},t)| & = & \displaystyle 0,\qquad \lim _{s\rightarrow \infty }|e(s+\unicode[STIX]{x1D70F},t)|=0\nonumber\\ \displaystyle \displaystyle \lim _{s\rightarrow \infty }|d^{\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}}u(s+\unicode[STIX]{x1D70F},t)| & = & \displaystyle 0,\qquad \lim _{s\rightarrow \infty }u^{\ast }\unicode[STIX]{x1D703}(s+\unicode[STIX]{x1D70F},t)=-{\mathcal{Q}}\,d\unicode[STIX]{x1D70F}+{\mathcal{T}}\,dt\nonumber\\ \displaystyle \displaystyle \lim _{s\rightarrow \infty }|\unicode[STIX]{x1D6FB}_{du}e(s+\unicode[STIX]{x1D70F},t)| & = & \displaystyle 0,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \lim _{s\rightarrow \infty }|\unicode[STIX]{x1D707}(s+\unicode[STIX]{x1D70F},t)| & = & \displaystyle 0,\qquad \lim _{s\rightarrow \infty }|e(s+\unicode[STIX]{x1D70F},t)|=0\nonumber\\ \displaystyle \displaystyle \lim _{s\rightarrow \infty }|d^{\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}}u(s+\unicode[STIX]{x1D70F},t)| & = & \displaystyle 0,\qquad \lim _{s\rightarrow \infty }u^{\ast }\unicode[STIX]{x1D703}(s+\unicode[STIX]{x1D70F},t)=-{\mathcal{Q}}\,d\unicode[STIX]{x1D70F}+{\mathcal{T}}\,dt\nonumber\\ \displaystyle \displaystyle \lim _{s\rightarrow \infty }|\unicode[STIX]{x1D6FB}_{du}e(s+\unicode[STIX]{x1D70F},t)| & = & \displaystyle 0,\nonumber\end{eqnarray}$$
and
 $$\begin{eqnarray}\displaystyle & & \displaystyle \lim _{s\rightarrow \infty }|\unicode[STIX]{x1D6FB}^{k}d^{\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}}u(s+\unicode[STIX]{x1D70F},t)|=0,\qquad \lim _{s\rightarrow \infty }|\unicode[STIX]{x1D6FB}^{k}u^{\ast }\unicode[STIX]{x1D703}(s+\unicode[STIX]{x1D70F},t)|=0\nonumber\\ \displaystyle & & \displaystyle \qquad \lim _{s\rightarrow \infty }|\unicode[STIX]{x1D6FB}_{du}^{k}e(s+\unicode[STIX]{x1D70F},t)|=0\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \lim _{s\rightarrow \infty }|\unicode[STIX]{x1D6FB}^{k}d^{\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}}u(s+\unicode[STIX]{x1D70F},t)|=0,\qquad \lim _{s\rightarrow \infty }|\unicode[STIX]{x1D6FB}^{k}u^{\ast }\unicode[STIX]{x1D703}(s+\unicode[STIX]{x1D70F},t)|=0\nonumber\\ \displaystyle & & \displaystyle \qquad \lim _{s\rightarrow \infty }|\unicode[STIX]{x1D6FB}_{du}^{k}e(s+\unicode[STIX]{x1D70F},t)|=0\end{eqnarray}$$
for all
![]() $k\geqslant 1$
, and all the limits are uniform for
$k\geqslant 1$
, and all the limits are uniform for
![]() $(\unicode[STIX]{x1D70F},t)$
on
$(\unicode[STIX]{x1D70F},t)$
on
![]() $K\times S^{1}$
with compact
$K\times S^{1}$
with compact
![]() $K\subset [0,\infty )$
.
$K\subset [0,\infty )$
.
In particular,
uniformly for
![]() $(\unicode[STIX]{x1D70F},t)$
in
$(\unicode[STIX]{x1D70F},t)$
in
![]() $C^{\infty }$
topology on
$C^{\infty }$
topology on
![]() $K\times S^{1}$
for any given compact
$K\times S^{1}$
for any given compact
![]() $K\subset [0,\infty )$
.
$K\subset [0,\infty )$
.
In the rest of the present paper, we add the following technical assumption of vanishing charge.
Hypothesis 9.7. (Charge vanishing)
Then the uniform convergence proved in this section ensures all the basic requirements (including the uniformly local tameness, precompactness, uniformly local coercive property and the locally asymptotically cylindrical property) of applying the three-interval method to prove exponential decay of
![]() $w$
at the end which we introduce in details in following sections.
$w$
at the end which we introduce in details in following sections.
10 Abstract framework of the three-interval method
In this section, we introduce a new method in proving exponential decay using the abstract framework of the three-interval method. In later Section 11.2, we apply the scheme to the normal bundle part. We remark that the method can deal with the case with an exponentially decaying perturbation too (see Theorem 10.11).
The three-interval method is based on the following analytic lemma.
Lemma 10.1. [Reference Mundet i Riera and TianMT, Lemma 9.4]
For a sequence of nonnegative numbers
![]() $\{x_{k}\}_{k=0,1,\ldots ,N}$
, if there exists some constant
$\{x_{k}\}_{k=0,1,\ldots ,N}$
, if there exists some constant
![]() $0<\unicode[STIX]{x1D6FE}<1/2$
such that
$0<\unicode[STIX]{x1D6FE}<1/2$
such that
for every
![]() $1\leqslant k\leqslant N-1$
, then it follows
$1\leqslant k\leqslant N-1$
, then it follows
where
![]() $\unicode[STIX]{x1D709}:=(1+\sqrt{1-4\unicode[STIX]{x1D6FE}^{2}})/2\unicode[STIX]{x1D6FE}$
.
$\unicode[STIX]{x1D709}:=(1+\sqrt{1-4\unicode[STIX]{x1D6FE}^{2}})/2\unicode[STIX]{x1D6FE}$
.
Remark 10.2.
(1) If we write
 $\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}(c):=1/(e^{c}+e^{-c})$
where
$\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}(c):=1/(e^{c}+e^{-c})$
where
 $c>0$
is uniquely determined by
$c>0$
is uniquely determined by
 $\unicode[STIX]{x1D6FE}$
, then the conclusion can be written into the exponential form
$\unicode[STIX]{x1D6FE}$
, then the conclusion can be written into the exponential form  $$\begin{eqnarray}x_{k}\leqslant x_{0}e^{-ck}+x_{N}e^{-c(N-k)}.\end{eqnarray}$$
$$\begin{eqnarray}x_{k}\leqslant x_{0}e^{-ck}+x_{N}e^{-c(N-k)}.\end{eqnarray}$$
(2) For an infinite nonnegative sequence
 $\{x_{k}\}_{k=0,1,\ldots }$
, if we have a uniform bound of in addition, then the exponential decay follows as
$\{x_{k}\}_{k=0,1,\ldots }$
, if we have a uniform bound of in addition, then the exponential decay follows as  $$\begin{eqnarray}x_{k}\leqslant x_{0}e^{-ck}.\end{eqnarray}$$
$$\begin{eqnarray}x_{k}\leqslant x_{0}e^{-ck}.\end{eqnarray}$$
The analysis of proving the exponential decay will be carried on a Banach bundle
![]() ${\mathcal{E}}\rightarrow [0,\infty )$
modeled by the Banach space
${\mathcal{E}}\rightarrow [0,\infty )$
modeled by the Banach space
![]() $\mathbb{E}$
, for which we mean every fiber
$\mathbb{E}$
, for which we mean every fiber
![]() $\mathbb{E}_{\unicode[STIX]{x1D70F}}$
is identified with the Banach space
$\mathbb{E}_{\unicode[STIX]{x1D70F}}$
is identified with the Banach space
![]() $\mathbb{E}$
smoothly depending on
$\mathbb{E}$
smoothly depending on
![]() $\unicode[STIX]{x1D70F}$
. We omit this identification if there is no way of confusion.
$\unicode[STIX]{x1D70F}$
. We omit this identification if there is no way of confusion.
First we emphasize the base
![]() $[0,\infty )$
is noncompact and carries a natural translation map for any positive number
$[0,\infty )$
is noncompact and carries a natural translation map for any positive number
![]() $r$
, which is
$r$
, which is
![]() $\unicode[STIX]{x1D70E}_{r}:\unicode[STIX]{x1D70F}\mapsto \unicode[STIX]{x1D70F}+r$
. We introduce the following definition which ensures us to study the sections in local trivialization after taking a subsequence.
$\unicode[STIX]{x1D70E}_{r}:\unicode[STIX]{x1D70F}\mapsto \unicode[STIX]{x1D70F}+r$
. We introduce the following definition which ensures us to study the sections in local trivialization after taking a subsequence.
Definition 10.3. Let
![]() ${\mathcal{E}}$
be a Banach bundle modeled with a Banach space
${\mathcal{E}}$
be a Banach bundle modeled with a Banach space
![]() $\mathbb{E}$
over
$\mathbb{E}$
over
![]() $[0,\infty )$
. Let
$[0,\infty )$
. Let
![]() $[a,b]\subset [0,\infty )$
be any given bounded interval and let
$[a,b]\subset [0,\infty )$
be any given bounded interval and let
![]() $s_{k}\rightarrow \infty$
be any given sequence. A tame family of trivialization over
$s_{k}\rightarrow \infty$
be any given sequence. A tame family of trivialization over
![]() $[a,b]$
relative to the sequence
$[a,b]$
relative to the sequence
![]() $s_{k}$
is defined to be a sequence of trivializations
$s_{k}$
is defined to be a sequence of trivializations
![]() $\{\unicode[STIX]{x1D6F7}_{k}\}:{\mathcal{E}}|_{[a,b]}\rightarrow [a,b]\times \mathbb{E}$
$\{\unicode[STIX]{x1D6F7}_{k}\}:{\mathcal{E}}|_{[a,b]}\rightarrow [a,b]\times \mathbb{E}$
for
![]() $k\geqslant 0$
satisfying the following: there exists a sufficiently large
$k\geqslant 0$
satisfying the following: there exists a sufficiently large
![]() $k_{0}>0$
such that for any
$k_{0}>0$
such that for any
![]() $k\geqslant k_{0}$
the bundle map
$k\geqslant k_{0}$
the bundle map
satisfies
for constants
![]() $C_{l}=C_{l}(|b-a|)$
depending only on
$C_{l}=C_{l}(|b-a|)$
depending only on
![]() $|b-a|$
,
$|b-a|$
,
![]() $l=0,1,\ldots .$
$l=0,1,\ldots .$
We call
![]() ${\mathcal{E}}$
uniformly locally tame, if it carries a tame family of trivializations over
${\mathcal{E}}$
uniformly locally tame, if it carries a tame family of trivializations over
![]() $[a,b]$
relative to the sequence
$[a,b]$
relative to the sequence
![]() $s_{k}$
for any given bounded interval
$s_{k}$
for any given bounded interval
![]() $[a,b]\subset [0,\infty )$
and a sequence
$[a,b]\subset [0,\infty )$
and a sequence
![]() $s_{k}\rightarrow \infty$
.
$s_{k}\rightarrow \infty$
.
Definition 10.4. Suppose
![]() ${\mathcal{E}}$
is uniformly locally tame. We say a connection
${\mathcal{E}}$
is uniformly locally tame. We say a connection
![]() $\unicode[STIX]{x1D6FB}$
on
$\unicode[STIX]{x1D6FB}$
on
![]() ${\mathcal{E}}$
is uniformly locally tame if the push-forward
${\mathcal{E}}$
is uniformly locally tame if the push-forward
![]() $(\unicode[STIX]{x1D6F7}_{k})_{\ast }\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D70F}}$
can be written as
$(\unicode[STIX]{x1D6F7}_{k})_{\ast }\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D70F}}$
can be written as
for any tame family
![]() $\{\unicode[STIX]{x1D6F7}_{k}\}$
so that
$\{\unicode[STIX]{x1D6F7}_{k}\}$
so that
![]() $\sup _{\unicode[STIX]{x1D70F}\in [a,b]}\Vert \unicode[STIX]{x1D6E4}_{k}(\unicode[STIX]{x1D70F})\Vert _{{\mathcal{L}}(\mathbb{E},\mathbb{E})}<C$
for some
$\sup _{\unicode[STIX]{x1D70F}\in [a,b]}\Vert \unicode[STIX]{x1D6E4}_{k}(\unicode[STIX]{x1D70F})\Vert _{{\mathcal{L}}(\mathbb{E},\mathbb{E})}<C$
for some
![]() $C>0$
independent of
$C>0$
independent of
![]() $k$
’s.
$k$
’s.
Definition 10.5. Consider a pair
![]() ${\mathcal{E}}_{2}\subset {\mathcal{E}}_{1}$
of uniformly locally tame bundles, and a bundle map
${\mathcal{E}}_{2}\subset {\mathcal{E}}_{1}$
of uniformly locally tame bundles, and a bundle map
![]() $B:{\mathcal{E}}_{2}\rightarrow {\mathcal{E}}_{1}$
. We say
$B:{\mathcal{E}}_{2}\rightarrow {\mathcal{E}}_{1}$
. We say
![]() $B$
is uniformly locally bounded, if for any compact set
$B$
is uniformly locally bounded, if for any compact set
![]() $[a,b]\subset [0,\infty )$
and any sequence
$[a,b]\subset [0,\infty )$
and any sequence
![]() $s_{k}\rightarrow \infty$
, there exists a subsequence, still denoted by
$s_{k}\rightarrow \infty$
, there exists a subsequence, still denoted by
![]() $s_{k}$
, a sufficiently large
$s_{k}$
, a sufficiently large
![]() $k_{0}>0$
and tame families
$k_{0}>0$
and tame families
![]() $\unicode[STIX]{x1D6F7}_{1,k}$
,
$\unicode[STIX]{x1D6F7}_{1,k}$
,
![]() $\unicode[STIX]{x1D6F7}_{2,k}$
such that for any
$\unicode[STIX]{x1D6F7}_{2,k}$
such that for any
![]() $k\geqslant 0$
$k\geqslant 0$
where
![]() $C$
is independent of
$C$
is independent of
![]() $k$
.
$k$
.
For a given locally tame pair
![]() ${\mathcal{E}}_{2}\subset {\mathcal{E}}_{1}$
, we denote by
${\mathcal{E}}_{2}\subset {\mathcal{E}}_{1}$
, we denote by
![]() ${\mathcal{L}}({\mathcal{E}}_{2},{\mathcal{E}}_{1})$
the set of bundle homomorphisms which are uniformly locally bounded.
${\mathcal{L}}({\mathcal{E}}_{2},{\mathcal{E}}_{1})$
the set of bundle homomorphisms which are uniformly locally bounded.
Lemma 10.6. If
![]() ${\mathcal{E}}_{1}$
,
${\mathcal{E}}_{1}$
,
![]() ${\mathcal{E}}_{2}$
are uniformly locally tame, then so is
${\mathcal{E}}_{2}$
are uniformly locally tame, then so is
![]() ${\mathcal{L}}({\mathcal{E}}_{2},{\mathcal{E}}_{1})$
.
${\mathcal{L}}({\mathcal{E}}_{2},{\mathcal{E}}_{1})$
.
Definition 10.7. Let
![]() ${\mathcal{E}}_{2}\subset {\mathcal{E}}_{1}$
be as above and let
${\mathcal{E}}_{2}\subset {\mathcal{E}}_{1}$
be as above and let
![]() $B\in {\mathcal{L}}({\mathcal{E}}_{2},{\mathcal{E}}_{1})$
. We say
$B\in {\mathcal{L}}({\mathcal{E}}_{2},{\mathcal{E}}_{1})$
. We say
![]() $B$
is precompact on
$B$
is precompact on
![]() $[0,\infty )$
if for any locally tame families
$[0,\infty )$
if for any locally tame families
![]() $\unicode[STIX]{x1D6F7}_{1}$
,
$\unicode[STIX]{x1D6F7}_{1}$
,
![]() $\unicode[STIX]{x1D6F7}_{2}$
, there exists a further subsequence such that
$\unicode[STIX]{x1D6F7}_{2}$
, there exists a further subsequence such that
![]() $\unicode[STIX]{x1D6F7}_{1,k_{0}+k}\circ B\circ \unicode[STIX]{x1D6F7}_{1,k_{0}}^{-1}$
converges to some
$\unicode[STIX]{x1D6F7}_{1,k_{0}+k}\circ B\circ \unicode[STIX]{x1D6F7}_{1,k_{0}}^{-1}$
converges to some
![]() $B_{\unicode[STIX]{x1D6F7}_{1}\unicode[STIX]{x1D6F7}_{2};\infty }\in {\mathcal{L}}(\unicode[STIX]{x1D6E4}([a,b]\times \mathbb{E}_{2}),\unicode[STIX]{x1D6E4}([a,b]\times \mathbb{E}_{1}))$
.
$B_{\unicode[STIX]{x1D6F7}_{1}\unicode[STIX]{x1D6F7}_{2};\infty }\in {\mathcal{L}}(\unicode[STIX]{x1D6E4}([a,b]\times \mathbb{E}_{2}),\unicode[STIX]{x1D6E4}([a,b]\times \mathbb{E}_{1}))$
.
Assume
![]() $B$
is a bundle map from
$B$
is a bundle map from
![]() ${\mathcal{E}}_{2}$
to
${\mathcal{E}}_{2}$
to
![]() ${\mathcal{E}}_{1}$
which is uniformly locally bounded, where
${\mathcal{E}}_{1}$
which is uniformly locally bounded, where
![]() ${\mathcal{E}}_{1}\supset {\mathcal{E}}_{2}$
are uniformly locally tame with tame families
${\mathcal{E}}_{1}\supset {\mathcal{E}}_{2}$
are uniformly locally tame with tame families
![]() $\unicode[STIX]{x1D6F7}_{1,k}$
,
$\unicode[STIX]{x1D6F7}_{1,k}$
,
![]() $\unicode[STIX]{x1D6F7}_{2,k}$
. We can write
$\unicode[STIX]{x1D6F7}_{2,k}$
. We can write
as a linear map from
![]() $\unicode[STIX]{x1D6E4}([a,b]\times \mathbb{E}_{2})$
to
$\unicode[STIX]{x1D6E4}([a,b]\times \mathbb{E}_{2})$
to
![]() $\unicode[STIX]{x1D6E4}([a,b]\times \mathbb{E}_{1})$
, since
$\unicode[STIX]{x1D6E4}([a,b]\times \mathbb{E}_{1})$
, since
![]() $\unicode[STIX]{x1D6FB}$
is uniformly locally tame.
$\unicode[STIX]{x1D6FB}$
is uniformly locally tame.
Next we introduce the following notion of coerciveness.
Definition 10.8. Let
![]() ${\mathcal{E}}_{1}$
,
${\mathcal{E}}_{1}$
,
![]() ${\mathcal{E}}_{2}$
be as above and
${\mathcal{E}}_{2}$
be as above and
![]() $B:{\mathcal{E}}_{2}\rightarrow {\mathcal{E}}_{1}$
be a uniformly locally bounded bundle map. We say the operator
$B:{\mathcal{E}}_{2}\rightarrow {\mathcal{E}}_{1}$
be a uniformly locally bounded bundle map. We say the operator
is uniformly locally coercive, if the following holds:
(1) for any pair of bounded closed intervals
 $I$
,
$I$
,
 $I^{\prime }$
with
$I^{\prime }$
with
 $I\subset \text{Int}\,I^{\prime }$
, (10.3)for a constant
$I\subset \text{Int}\,I^{\prime }$
, (10.3)for a constant $$\begin{eqnarray}\Vert \unicode[STIX]{x1D701}\Vert _{L^{2}(I,{\mathcal{E}}_{2})}\leqslant C(I,I^{\prime })(\Vert \unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D701}+B\unicode[STIX]{x1D701}\Vert _{L^{2}(I^{\prime },{\mathcal{E}}_{1})}+\Vert \unicode[STIX]{x1D701}\Vert _{L^{2}(I^{\prime },{\mathcal{E}}_{1})})\end{eqnarray}$$
$$\begin{eqnarray}\Vert \unicode[STIX]{x1D701}\Vert _{L^{2}(I,{\mathcal{E}}_{2})}\leqslant C(I,I^{\prime })(\Vert \unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D701}+B\unicode[STIX]{x1D701}\Vert _{L^{2}(I^{\prime },{\mathcal{E}}_{1})}+\Vert \unicode[STIX]{x1D701}\Vert _{L^{2}(I^{\prime },{\mathcal{E}}_{1})})\end{eqnarray}$$
 $C(I,I^{\prime })$
depending only on
$C(I,I^{\prime })$
depending only on
 $I$
,
$I$
,
 $I^{\prime }$
but independent of
$I^{\prime }$
but independent of
 $\unicode[STIX]{x1D701}$
;
$\unicode[STIX]{x1D701}$
;(2) if for given bounded sequence
 $\unicode[STIX]{x1D701}_{k}\in \unicode[STIX]{x1D6E4}({\mathcal{E}}_{2})$
satisfying with
$\unicode[STIX]{x1D701}_{k}\in \unicode[STIX]{x1D6E4}({\mathcal{E}}_{2})$
satisfying with $$\begin{eqnarray}\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D701}_{k}+B\unicode[STIX]{x1D701}_{k}=L_{k}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D701}_{k}+B\unicode[STIX]{x1D701}_{k}=L_{k}\end{eqnarray}$$
 $|L_{k}(\unicode[STIX]{x1D70F})|_{{\mathcal{E}}_{1}}$
bounded on a given compact subset
$|L_{k}(\unicode[STIX]{x1D70F})|_{{\mathcal{E}}_{1}}$
bounded on a given compact subset
 $K\subset [0,\infty )$
, there exists a subsequence, still denoted by
$K\subset [0,\infty )$
, there exists a subsequence, still denoted by
 $\unicode[STIX]{x1D701}_{k}$
, that uniformly converges in
$\unicode[STIX]{x1D701}_{k}$
, that uniformly converges in
 ${\mathcal{E}}_{2}$
.
${\mathcal{E}}_{2}$
.
Remark 10.9. Let
![]() $E\rightarrow [0,\infty )\times S$
be a (finite-dimensional) vector bundle and denote by
$E\rightarrow [0,\infty )\times S$
be a (finite-dimensional) vector bundle and denote by
![]() $W^{k,2}(E)$
the set of
$W^{k,2}(E)$
the set of
![]() $W^{k,2}$
-section of
$W^{k,2}$
-section of
![]() $E$
and
$E$
and
![]() $L^{2}(E)$
the set of
$L^{2}(E)$
the set of
![]() $L^{2}$
-sections. Let
$L^{2}$
-sections. Let
![]() $D:L^{2}(E)\rightarrow L^{2}(E)$
be a first-order elliptic operator with cylindrical end. Denote by
$D:L^{2}(E)\rightarrow L^{2}(E)$
be a first-order elliptic operator with cylindrical end. Denote by
![]() $i_{\unicode[STIX]{x1D70F}}:S\rightarrow [0,\infty )\times S$
the natural inclusion map. Then there is a natural pair of Banach bundles
$i_{\unicode[STIX]{x1D70F}}:S\rightarrow [0,\infty )\times S$
the natural inclusion map. Then there is a natural pair of Banach bundles
![]() ${\mathcal{E}}_{2}\subset {\mathcal{E}}_{1}$
over
${\mathcal{E}}_{2}\subset {\mathcal{E}}_{1}$
over
![]() $[0,\infty )$
associated to
$[0,\infty )$
associated to
![]() $E$
, whose fiber is given by
$E$
, whose fiber is given by
![]() ${\mathcal{E}}_{1,\unicode[STIX]{x1D70F}}=L^{2}(i_{\unicode[STIX]{x1D70F}}^{\ast }E)$
,
${\mathcal{E}}_{1,\unicode[STIX]{x1D70F}}=L^{2}(i_{\unicode[STIX]{x1D70F}}^{\ast }E)$
,
![]() ${\mathcal{E}}_{2,\unicode[STIX]{x1D70F}}=W^{1,2}(i_{\unicode[STIX]{x1D70F}}^{\ast }E)$
. Furthermore, assume
${\mathcal{E}}_{2,\unicode[STIX]{x1D70F}}=W^{1,2}(i_{\unicode[STIX]{x1D70F}}^{\ast }E)$
. Furthermore, assume
![]() ${\mathcal{E}}_{i}$
for
${\mathcal{E}}_{i}$
for
![]() $i=1,2$
is uniformly local tame if
$i=1,2$
is uniformly local tame if
![]() $S$
is a compact manifold (without boundary). Then
$S$
is a compact manifold (without boundary). Then
![]() $D$
is uniformly locally coercive, which follows from the elliptic bootstrapping and the Sobolev’s embedding.
$D$
is uniformly locally coercive, which follows from the elliptic bootstrapping and the Sobolev’s embedding.
Finally we introduce the notion of asymptotically cylindrical operator
![]() $B$
.
$B$
.
Definition 10.10. We call
![]() $B$
locally asymptotically cylindrical if the following holds: any subsequence limit
$B$
locally asymptotically cylindrical if the following holds: any subsequence limit
![]() $B_{\unicode[STIX]{x1D6F7}_{1}\unicode[STIX]{x1D6F7}_{2};\infty }$
appearing in Definition 10.7 is a constant section, and
$B_{\unicode[STIX]{x1D6F7}_{1}\unicode[STIX]{x1D6F7}_{2};\infty }$
appearing in Definition 10.7 is a constant section, and
![]() $\Vert B_{\unicode[STIX]{x1D6F7}_{1}\unicode[STIX]{x1D6F7}_{2},k}-\unicode[STIX]{x1D6F7}_{2,k_{0}+k}\circ B\circ \unicode[STIX]{x1D6F7}_{1,k_{0}}^{-1}\Vert _{{\mathcal{L}}(\mathbb{E}_{i},\mathbb{E}_{i})}$
converges to zero as
$\Vert B_{\unicode[STIX]{x1D6F7}_{1}\unicode[STIX]{x1D6F7}_{2},k}-\unicode[STIX]{x1D6F7}_{2,k_{0}+k}\circ B\circ \unicode[STIX]{x1D6F7}_{1,k_{0}}^{-1}\Vert _{{\mathcal{L}}(\mathbb{E}_{i},\mathbb{E}_{i})}$
converges to zero as
![]() $k\rightarrow \infty$
for both
$k\rightarrow \infty$
for both
![]() $i=1,2$
.
$i=1,2$
.
Now we specialize to the case of Hilbert bundles
![]() ${\mathcal{E}}_{2}\subset {\mathcal{E}}_{1}$
over
${\mathcal{E}}_{2}\subset {\mathcal{E}}_{1}$
over
![]() $[0,\infty )$
and assume that
$[0,\infty )$
and assume that
![]() ${\mathcal{E}}_{1}$
carries a connection which is compatible with the Hilbert inner product of
${\mathcal{E}}_{1}$
carries a connection which is compatible with the Hilbert inner product of
![]() ${\mathcal{E}}_{1}$
. We denote by
${\mathcal{E}}_{1}$
. We denote by
![]() $\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D70F}}$
the associated covariant derivative. We assume that
$\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D70F}}$
the associated covariant derivative. We assume that
![]() $\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D70F}}$
is uniformly locally tame.
$\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D70F}}$
is uniformly locally tame.
Denote by
![]() $L^{2}([a,b];{\mathcal{E}}_{i})$
the space of
$L^{2}([a,b];{\mathcal{E}}_{i})$
the space of
![]() $L^{2}$
-sections
$L^{2}$
-sections
![]() $\unicode[STIX]{x1D701}$
of
$\unicode[STIX]{x1D701}$
of
![]() ${\mathcal{E}}_{i}$
over
${\mathcal{E}}_{i}$
over
![]() $[a,b]$
, that is, those satisfying
$[a,b]$
, that is, those satisfying
where
![]() $|\unicode[STIX]{x1D701}(\unicode[STIX]{x1D70F})|_{{\mathcal{E}}_{i}}$
is the norm with respect to the given Hilbert bundle structure of
$|\unicode[STIX]{x1D701}(\unicode[STIX]{x1D70F})|_{{\mathcal{E}}_{i}}$
is the norm with respect to the given Hilbert bundle structure of
![]() ${\mathcal{E}}_{i}$
.
${\mathcal{E}}_{i}$
.
Theorem 10.11. (Three-interval method)
Assume
![]() ${\mathcal{E}}_{2}\subset {\mathcal{E}}_{1}$
is a pair of Hilbert bundles over
${\mathcal{E}}_{2}\subset {\mathcal{E}}_{1}$
is a pair of Hilbert bundles over
![]() $[0,\infty )$
with fibers
$[0,\infty )$
with fibers
![]() $\mathbb{E}_{2}$
and
$\mathbb{E}_{2}$
and
![]() $\mathbb{E}_{1}$
, and
$\mathbb{E}_{1}$
, and
![]() $\mathbb{E}_{2}\subset \mathbb{E}_{1}$
is dense. Let
$\mathbb{E}_{2}\subset \mathbb{E}_{1}$
is dense. Let
![]() $B$
be a section of the associated bundle
$B$
be a section of the associated bundle
![]() ${\mathcal{L}}({\mathcal{E}}_{2},{\mathcal{E}}_{1})$
and
${\mathcal{L}}({\mathcal{E}}_{2},{\mathcal{E}}_{1})$
and
![]() $L\in \unicode[STIX]{x1D6E4}({\mathcal{E}}_{1})$
. We assume the following:
$L\in \unicode[STIX]{x1D6E4}({\mathcal{E}}_{1})$
. We assume the following:
(1) there exists a covariant derivative
 $\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D70F}}$
that preserves the Hilbert structure;
$\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D70F}}$
that preserves the Hilbert structure;(2)
 ${\mathcal{E}}_{i}$
for
${\mathcal{E}}_{i}$
for
 $i=1,2$
are uniformly locally tame;
$i=1,2$
are uniformly locally tame;(3)
 $B$
is precompact, uniformly locally coercive and asymptotically cylindrical;
$B$
is precompact, uniformly locally coercive and asymptotically cylindrical;(4) every subsequence limit
 $B_{\infty }$
is a self-adjoint unbounded operator on
$B_{\infty }$
is a self-adjoint unbounded operator on
 $\mathbb{E}_{1}$
with its domain
$\mathbb{E}_{1}$
with its domain
 $\mathbb{E}_{2}$
, and satisfies
$\mathbb{E}_{2}$
, and satisfies
 $\ker B_{\infty }=\{0\}$
;
$\ker B_{\infty }=\{0\}$
;(5) there exists some positive number
 $\unicode[STIX]{x1D6FF}$
such that any subsequence limiting operator
$\unicode[STIX]{x1D6FF}$
such that any subsequence limiting operator
 $B_{\infty }$
of the above mentioned precompact family has all their eigenvalues
$B_{\infty }$
of the above mentioned precompact family has all their eigenvalues
 $\unicode[STIX]{x1D706}$
satisfying
$\unicode[STIX]{x1D706}$
satisfying
 $|\unicode[STIX]{x1D706}|>\unicode[STIX]{x1D6FF}$
;
$|\unicode[STIX]{x1D706}|>\unicode[STIX]{x1D6FF}$
;(6) there exists some
 $R_{0}>0$
,
$R_{0}>0$
,
 $C_{0}>0$
and
$C_{0}>0$
and
 $\unicode[STIX]{x1D6FF}_{0}>\unicode[STIX]{x1D6FF}$
such that for all
$\unicode[STIX]{x1D6FF}_{0}>\unicode[STIX]{x1D6FF}$
such that for all $$\begin{eqnarray}|L(\unicode[STIX]{x1D70F})|_{{\mathcal{E}}_{1,\unicode[STIX]{x1D70F}}}\leqslant C_{0}e^{-\unicode[STIX]{x1D6FF}_{0}\unicode[STIX]{x1D70F}}\end{eqnarray}$$
$$\begin{eqnarray}|L(\unicode[STIX]{x1D70F})|_{{\mathcal{E}}_{1,\unicode[STIX]{x1D70F}}}\leqslant C_{0}e^{-\unicode[STIX]{x1D6FF}_{0}\unicode[STIX]{x1D70F}}\end{eqnarray}$$
 $\unicode[STIX]{x1D70F}\geqslant R_{0}$
.
$\unicode[STIX]{x1D70F}\geqslant R_{0}$
.
Then for any (smooth) section
![]() $\unicode[STIX]{x1D701}\in \unicode[STIX]{x1D6E4}({\mathcal{E}}_{2})$
with
$\unicode[STIX]{x1D701}\in \unicode[STIX]{x1D6E4}({\mathcal{E}}_{2})$
with
and satisfying the equation
there exist some constants
![]() $R$
,
$R$
,
![]() $C>0$
such that for any
$C>0$
such that for any
![]() $\unicode[STIX]{x1D70F}>R$
,
$\unicode[STIX]{x1D70F}>R$
,
Proof. We divide
![]() $[0,\infty )$
into the union of unit intervals
$[0,\infty )$
into the union of unit intervals
![]() $I_{k}:=[k,k+1]$
for
$I_{k}:=[k,k+1]$
for
![]() $k=0,1,\ldots .$
We first prove the exponential decay of
$k=0,1,\ldots .$
We first prove the exponential decay of
![]() $\Vert \unicode[STIX]{x1D701}\Vert _{L^{2}(I_{k};{\mathcal{E}}_{1})}^{2}$
to zero as
$\Vert \unicode[STIX]{x1D701}\Vert _{L^{2}(I_{k};{\mathcal{E}}_{1})}^{2}$
to zero as
![]() $k\rightarrow \infty$
. By Lemma 10.1 and Remark 10.2, it is enough to prove that for the function
$k\rightarrow \infty$
. By Lemma 10.1 and Remark 10.2, it is enough to prove that for the function
![]() $\unicode[STIX]{x1D6FE}(c)=1/(e^{c}+e^{-c})$
as in Remark 10.2 we have
$\unicode[STIX]{x1D6FE}(c)=1/(e^{c}+e^{-c})$
as in Remark 10.2 we have
for every
![]() $k=1,2,\ldots$
for some choice of
$k=1,2,\ldots$
for some choice of
![]() $0<\unicode[STIX]{x1D6FF}<1$
. For the simplicity of notation and also because we use only the norms on
$0<\unicode[STIX]{x1D6FF}<1$
. For the simplicity of notation and also because we use only the norms on
![]() ${\mathcal{E}}_{1}$
(but applied to
${\mathcal{E}}_{1}$
(but applied to
![]() $\unicode[STIX]{x1D701}\in {\mathcal{E}}_{2}$
) in the discussion below, we just denote
$\unicode[STIX]{x1D701}\in {\mathcal{E}}_{2}$
) in the discussion below, we just denote
for any given interval
![]() $[a,b]$
.
$[a,b]$
.
If inequality (10.6) does not hold for every
![]() $k$
, we collect all the
$k$
, we collect all the
![]() $k$
’s that reverse the direction of the inequality. If such
$k$
’s that reverse the direction of the inequality. If such
![]() $k$
’s are finitely many, that is, (10.6) holds after some large
$k$
’s are finitely many, that is, (10.6) holds after some large
![]() $k_{0}$
, then we still get the exponential estimate as the theorem claims.
$k_{0}$
, then we still get the exponential estimate as the theorem claims.
Otherwise, there are infinitely many such three-intervals, which we enumerate by
![]() $I_{I}^{l_{k}}:=[l_{k},l_{k}+1]$
,
$I_{I}^{l_{k}}:=[l_{k},l_{k}+1]$
,
![]() $I_{II}^{l_{k}}:=[l_{k}+1,l_{k}+2]$
,
$I_{II}^{l_{k}}:=[l_{k}+1,l_{k}+2]$
,
![]() $I_{III}^{l_{k}}:=[l_{k}+2,l_{k}+3]$
,
$I_{III}^{l_{k}}:=[l_{k}+2,l_{k}+3]$
,
![]() $k=1,2,\ldots ,$
such that
$k=1,2,\ldots ,$
such that
Before we deal with this case, we first remark that this hypothesis in particular implies
![]() $\unicode[STIX]{x1D701}\not \equiv 0$
on
$\unicode[STIX]{x1D701}\not \equiv 0$
on
![]() $I^{l_{k}}:=I_{I}^{l_{k}}\cup I_{II}^{l_{k}}\cup I_{III}^{l_{k}}$
, that is,
$I^{l_{k}}:=I_{I}^{l_{k}}\cup I_{II}^{l_{k}}\cup I_{III}^{l_{k}}$
, that is,
![]() $\Vert \unicode[STIX]{x1D701}\Vert _{L^{\infty }(I^{l_{k}})}\neq 0$
.
$\Vert \unicode[STIX]{x1D701}\Vert _{L^{\infty }(I^{l_{k}})}\neq 0$
.
If there exists some uniform constant
![]() $C_{1}>0$
such that on each such three-intervals
$C_{1}>0$
such that on each such three-intervals
it follows that
Here
![]() $C=C_{1}e^{-\unicode[STIX]{x1D6FF}}$
is purely a constant depending only on
$C=C_{1}e^{-\unicode[STIX]{x1D6FF}}$
is purely a constant depending only on
![]() $\unicode[STIX]{x1D6FF}$
which will be determined at the end. From now on, various constants
$\unicode[STIX]{x1D6FF}$
which will be determined at the end. From now on, various constants
![]() $C$
appearing below may vary but be independent of
$C$
appearing below may vary but be independent of
![]() $\unicode[STIX]{x1D701}$
.
$\unicode[STIX]{x1D701}$
.
Recall that under our assumption we have infinitely many intervals that satisfy (10.6), and the exponential inequality (10.8). If the union of such intervals
![]() $[l_{k}+1,l_{k}+2]$
is connected after some point, then we already get our conclusion from (10.9) since every interval becomes a middle interval (of the form
$[l_{k}+1,l_{k}+2]$
is connected after some point, then we already get our conclusion from (10.9) since every interval becomes a middle interval (of the form
![]() $[l_{k}+1,l_{k}+2]$
) in such three-intervals.
$[l_{k}+1,l_{k}+2]$
) in such three-intervals.
Otherwise the set of
![]() $k$
’s that satisfy (10.6) form a sequence of clusters,
$k$
’s that satisfy (10.6) form a sequence of clusters,
for the sequence
![]() $l_{1}$
,
$l_{1}$
,
![]() $l_{2},\ldots ,l_{k},\ldots$
such that
$l_{2},\ldots ,l_{k},\ldots$
such that
![]() $l_{k+1}>l_{k}+N_{k}$
and (10.6) holds on each element contained in each cluster.
$l_{k+1}>l_{k}+N_{k}$
and (10.6) holds on each element contained in each cluster.
We remark that each cluster has the farthest left interval
![]() $[l_{k}+1,l_{k}+2]$
as the middle interval in
$[l_{k}+1,l_{k}+2]$
as the middle interval in
![]() $I^{l_{k}}$
, and the farthest right interval
$I^{l_{k}}$
, and the farthest right interval
![]() $[l_{k}+N+2,l_{k}+N+3]$
as the middle interval in
$[l_{k}+N+2,l_{k}+N+3]$
as the middle interval in
![]() $I^{l_{k+1}}$
. (See Figure 1.)
$I^{l_{k+1}}$
. (See Figure 1.)

Figure 1. The three-interval method.
Then from (10.9), we derive
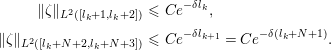 $$\begin{eqnarray}\displaystyle \Vert \unicode[STIX]{x1D701}\Vert _{L^{2}([l_{k}+1,l_{k}+2])} & {\leqslant} & \displaystyle Ce^{-\unicode[STIX]{x1D6FF}l_{k}},\nonumber\\ \displaystyle \Vert \unicode[STIX]{x1D701}\Vert _{L^{2}([l_{k}+N+2,l_{k}+N+3])} & {\leqslant} & \displaystyle Ce^{-\unicode[STIX]{x1D6FF}l_{k+1}}=Ce^{-\unicode[STIX]{x1D6FF}(l_{k}+N+1)}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \Vert \unicode[STIX]{x1D701}\Vert _{L^{2}([l_{k}+1,l_{k}+2])} & {\leqslant} & \displaystyle Ce^{-\unicode[STIX]{x1D6FF}l_{k}},\nonumber\\ \displaystyle \Vert \unicode[STIX]{x1D701}\Vert _{L^{2}([l_{k}+N+2,l_{k}+N+3])} & {\leqslant} & \displaystyle Ce^{-\unicode[STIX]{x1D6FF}l_{k+1}}=Ce^{-\unicode[STIX]{x1D6FF}(l_{k}+N+1)}.\nonumber\end{eqnarray}$$
Combining them and Lemma 10.1, we get the following estimate for
![]() $l_{k}+1\leqslant l\leqslant l_{k}+N+2$
,
$l_{k}+1\leqslant l\leqslant l_{k}+N+2$
,
 $$\begin{eqnarray}\displaystyle \Vert \unicode[STIX]{x1D701}\Vert _{L^{2}([l,l+1])} & {\leqslant} & \displaystyle \Vert \unicode[STIX]{x1D701}\Vert _{L^{2}([l_{k}+1,l_{k}+2])}e^{-\unicode[STIX]{x1D6FF}(l-(l_{k}+1))}\nonumber\\ \displaystyle & & \displaystyle +\,\Vert \unicode[STIX]{x1D701}\Vert _{L^{2}([l_{k}+N+2,l_{k}+N+3])}e^{-\unicode[STIX]{x1D6FF}(l_{k}+N+2-l)}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle Ce^{-\unicode[STIX]{x1D6FF}l_{k}}e^{-\unicode[STIX]{x1D6FF}(l-(l_{k}+1))}+Ce^{-\unicode[STIX]{x1D6FF}(l_{k}+N+1)}e^{-\unicode[STIX]{x1D6FF}(l_{k}+N+2-l)}\nonumber\\ \displaystyle & = & \displaystyle Ce^{\unicode[STIX]{x1D6FF}}(e^{-\unicode[STIX]{x1D6FF}l}+e^{-\unicode[STIX]{x1D6FF}(2l_{k}+2N+4-l)})\leqslant (2Ce^{\unicode[STIX]{x1D6FF}})e^{-\unicode[STIX]{x1D6FF}l}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \Vert \unicode[STIX]{x1D701}\Vert _{L^{2}([l,l+1])} & {\leqslant} & \displaystyle \Vert \unicode[STIX]{x1D701}\Vert _{L^{2}([l_{k}+1,l_{k}+2])}e^{-\unicode[STIX]{x1D6FF}(l-(l_{k}+1))}\nonumber\\ \displaystyle & & \displaystyle +\,\Vert \unicode[STIX]{x1D701}\Vert _{L^{2}([l_{k}+N+2,l_{k}+N+3])}e^{-\unicode[STIX]{x1D6FF}(l_{k}+N+2-l)}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle Ce^{-\unicode[STIX]{x1D6FF}l_{k}}e^{-\unicode[STIX]{x1D6FF}(l-(l_{k}+1))}+Ce^{-\unicode[STIX]{x1D6FF}(l_{k}+N+1)}e^{-\unicode[STIX]{x1D6FF}(l_{k}+N+2-l)}\nonumber\\ \displaystyle & = & \displaystyle Ce^{\unicode[STIX]{x1D6FF}}(e^{-\unicode[STIX]{x1D6FF}l}+e^{-\unicode[STIX]{x1D6FF}(2l_{k}+2N+4-l)})\leqslant (2Ce^{\unicode[STIX]{x1D6FF}})e^{-\unicode[STIX]{x1D6FF}l}.\nonumber\end{eqnarray}$$
Thus on each such cluster, we have exponential decay with the presumed rate
![]() $\unicode[STIX]{x1D6FF}$
as claimed in the theorem.
$\unicode[STIX]{x1D6FF}$
as claimed in the theorem.
Now if there is no such uniform
![]() $C=C_{1}$
for which (10.8) holds, then we can find a sequence of constants
$C=C_{1}$
for which (10.8) holds, then we can find a sequence of constants
![]() $C_{k}\rightarrow \infty$
and a subsequence of such three-intervals
$C_{k}\rightarrow \infty$
and a subsequence of such three-intervals
![]() $\{I^{l_{k}}\}$
, still denoted by
$\{I^{l_{k}}\}$
, still denoted by
![]() $l_{k}$
, such that
$l_{k}$
, such that
We can further choose a subsequence, but still denoted by
![]() $l_{k}$
, so that
$l_{k}$
, so that
![]() $l_{k}+3<l_{k+1}$
, that is, the intervals do not intersect one another.
$l_{k}+3<l_{k+1}$
, that is, the intervals do not intersect one another.
We translate the sections
![]() $\unicode[STIX]{x1D701}_{k}:=\unicode[STIX]{x1D701}|_{[l_{k},l_{k}+3]}$
and consider the sections
$\unicode[STIX]{x1D701}_{k}:=\unicode[STIX]{x1D701}|_{[l_{k},l_{k}+3]}$
and consider the sections
![]() $\widetilde{\unicode[STIX]{x1D701}}_{k}$
defined on
$\widetilde{\unicode[STIX]{x1D701}}_{k}$
defined on
![]() $[0,3]$
given by
$[0,3]$
given by
Then (10.10) becomes
If we consider the translations of
![]() $L$
given by
$L$
given by
![]() $\widetilde{L}_{k}(\unicode[STIX]{x1D70F},t)=L(\unicode[STIX]{x1D70F}+l_{k},t)$
, then
$\widetilde{L}_{k}(\unicode[STIX]{x1D70F},t)=L(\unicode[STIX]{x1D70F}+l_{k},t)$
, then
for
![]() $\unicode[STIX]{x1D70F}\geqslant 0$
. It follows that
$\unicode[STIX]{x1D70F}\geqslant 0$
. It follows that
![]() $\widetilde{\unicode[STIX]{x1D701}}_{k}$
satisfies the equation
$\widetilde{\unicode[STIX]{x1D701}}_{k}$
satisfies the equation
We now rescale (10.13) by dividing it by
![]() $\Vert \widetilde{\unicode[STIX]{x1D701}}_{k}\Vert _{L^{\infty }([0,3])}$
, which cannot vanish by the standing hypothesis as we remarked right below (10.7), and consider the rescaled sequence
$\Vert \widetilde{\unicode[STIX]{x1D701}}_{k}\Vert _{L^{\infty }([0,3])}$
, which cannot vanish by the standing hypothesis as we remarked right below (10.7), and consider the rescaled sequence
We have now
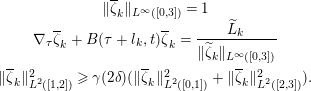 $$\begin{eqnarray}\begin{array}{@{}c@{}}\Vert \overline{\unicode[STIX]{x1D701}}_{k}\Vert _{L^{\infty }([0,3])}=1\\ \displaystyle \unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D70F}}\overline{\unicode[STIX]{x1D701}}_{k}+B(\unicode[STIX]{x1D70F}+l_{k},t)\overline{\unicode[STIX]{x1D701}}_{k}=\frac{\widetilde{L}_{k}}{\Vert \widetilde{\unicode[STIX]{x1D701}}_{k}\Vert _{L^{\infty }([0,3])}}\\ \Vert \overline{\unicode[STIX]{x1D701}}_{k}\Vert _{L^{2}([1,2])}^{2}\geqslant \unicode[STIX]{x1D6FE}(2\unicode[STIX]{x1D6FF})(\Vert \overline{\unicode[STIX]{x1D701}}_{k}\Vert _{L^{2}([0,1])}^{2}+\Vert \overline{\unicode[STIX]{x1D701}}_{k}\Vert _{L^{2}([2,3])}^{2}).\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}c@{}}\Vert \overline{\unicode[STIX]{x1D701}}_{k}\Vert _{L^{\infty }([0,3])}=1\\ \displaystyle \unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D70F}}\overline{\unicode[STIX]{x1D701}}_{k}+B(\unicode[STIX]{x1D70F}+l_{k},t)\overline{\unicode[STIX]{x1D701}}_{k}=\frac{\widetilde{L}_{k}}{\Vert \widetilde{\unicode[STIX]{x1D701}}_{k}\Vert _{L^{\infty }([0,3])}}\\ \Vert \overline{\unicode[STIX]{x1D701}}_{k}\Vert _{L^{2}([1,2])}^{2}\geqslant \unicode[STIX]{x1D6FE}(2\unicode[STIX]{x1D6FF})(\Vert \overline{\unicode[STIX]{x1D701}}_{k}\Vert _{L^{2}([0,1])}^{2}+\Vert \overline{\unicode[STIX]{x1D701}}_{k}\Vert _{L^{2}([2,3])}^{2}).\end{array}\end{eqnarray}$$
From (10.11) and (10.12), we get
and then by our assumption that
![]() $C_{k}\rightarrow \infty$
, we prove that the right-hand side of (10.14) converges to zero as
$C_{k}\rightarrow \infty$
, we prove that the right-hand side of (10.14) converges to zero as
![]() $k\rightarrow \infty$
.
$k\rightarrow \infty$
.
Since
![]() $B$
is assumed to be precompact, we get a limiting operator
$B$
is assumed to be precompact, we get a limiting operator
![]() $B_{\infty }$
after taking a subsequence (in a trivialization).
$B_{\infty }$
after taking a subsequence (in a trivialization).
On the other hand, since
![]() $B$
is locally coercive, there exists
$B$
is locally coercive, there exists
![]() $\overline{\unicode[STIX]{x1D701}}_{\infty }$
such that
$\overline{\unicode[STIX]{x1D701}}_{\infty }$
such that
![]() $\bar{\unicode[STIX]{x1D701}}_{k}\rightarrow \overline{\unicode[STIX]{x1D701}}_{\infty }$
uniformly converges in
$\bar{\unicode[STIX]{x1D701}}_{k}\rightarrow \overline{\unicode[STIX]{x1D701}}_{\infty }$
uniformly converges in
![]() ${\mathcal{E}}_{2}$
and
${\mathcal{E}}_{2}$
and
![]() $\overline{\unicode[STIX]{x1D701}}_{\infty }$
satisfies
$\overline{\unicode[STIX]{x1D701}}_{\infty }$
satisfies
and
Since
![]() $\Vert \overline{\unicode[STIX]{x1D701}}_{\infty }\Vert _{L^{\infty }([0,3]\times S^{1})}=1$
,
$\Vert \overline{\unicode[STIX]{x1D701}}_{\infty }\Vert _{L^{\infty }([0,3]\times S^{1})}=1$
,
![]() $\overline{\unicode[STIX]{x1D701}}_{\infty }\not \equiv 0$
. Recall that
$\overline{\unicode[STIX]{x1D701}}_{\infty }\not \equiv 0$
. Recall that
![]() $B_{\infty }$
is assumed to be a (unbounded) self-adjoint operator on
$B_{\infty }$
is assumed to be a (unbounded) self-adjoint operator on
![]() $\mathbb{E}_{1}$
with its domain
$\mathbb{E}_{1}$
with its domain
![]() $\mathbb{E}_{2}$
. Let
$\mathbb{E}_{2}$
. Let
![]() $\{e_{i}\}$
be its orthonormal eigenbasis of
$\{e_{i}\}$
be its orthonormal eigenbasis of
![]() $\mathbb{E}_{1}$
with respect to
$\mathbb{E}_{1}$
with respect to
![]() $B_{\infty }$
. We consider the eigenfunction expansion of
$B_{\infty }$
. We consider the eigenfunction expansion of
![]() $\overline{\unicode[STIX]{x1D701}}_{\infty }(\unicode[STIX]{x1D70F},\cdot )$
and write
$\overline{\unicode[STIX]{x1D701}}_{\infty }(\unicode[STIX]{x1D70F},\cdot )$
and write
for each
![]() $\unicode[STIX]{x1D70F}\in [0,3]$
, where
$\unicode[STIX]{x1D70F}\in [0,3]$
, where
![]() $e_{i}$
are the eigenfunctions of
$e_{i}$
are the eigenfunctions of
![]() $B$
associated to the eigenvalue
$B$
associated to the eigenvalue
![]() $\unicode[STIX]{x1D706}_{i}$
with
$\unicode[STIX]{x1D706}_{i}$
with
By plugging
![]() $\overline{\unicode[STIX]{x1D701}}_{\infty }$
into (10.15), we derive
$\overline{\unicode[STIX]{x1D701}}_{\infty }$
into (10.15), we derive
It follows that
for some constants
![]() $c_{i}$
and hence
$c_{i}$
and hence
with the function determined by the function
Equivalently, we obtain
(This is how the function
![]() $\unicode[STIX]{x1D6FE}$
becomes relevant to this three-interval argument. We note that
$\unicode[STIX]{x1D6FE}$
becomes relevant to this three-interval argument. We note that
![]() $\unicode[STIX]{x1D6FE}$
is an even function.) We compute
$\unicode[STIX]{x1D6FE}$
is an even function.) We compute
 $$\begin{eqnarray}\displaystyle \Vert \overline{\unicode[STIX]{x1D701}}_{\infty }\Vert _{L^{2}([k,k+1])}^{2} & = & \displaystyle \int _{[k,k+1]}\Vert \overline{\unicode[STIX]{x1D701}}_{\infty }\Vert _{L^{2}(S^{1})}^{2}\,d\unicode[STIX]{x1D70F}\nonumber\\ \displaystyle & = & \displaystyle \int _{[k,k+1]}\mathop{\sum }_{i}|a_{i}(\unicode[STIX]{x1D70F})|^{2}\,d\unicode[STIX]{x1D70F}=\mathop{\sum }_{i}\Vert a_{i}\Vert _{L^{2}([k,k+1])}^{2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \Vert \overline{\unicode[STIX]{x1D701}}_{\infty }\Vert _{L^{2}([k,k+1])}^{2} & = & \displaystyle \int _{[k,k+1]}\Vert \overline{\unicode[STIX]{x1D701}}_{\infty }\Vert _{L^{2}(S^{1})}^{2}\,d\unicode[STIX]{x1D70F}\nonumber\\ \displaystyle & = & \displaystyle \int _{[k,k+1]}\mathop{\sum }_{i}|a_{i}(\unicode[STIX]{x1D70F})|^{2}\,d\unicode[STIX]{x1D70F}=\mathop{\sum }_{i}\Vert a_{i}\Vert _{L^{2}([k,k+1])}^{2}.\nonumber\end{eqnarray}$$
By the monotonically decreasing property of
![]() $\unicode[STIX]{x1D6FE}$
for
$\unicode[STIX]{x1D6FE}$
for
![]() $c>0$
, this and (10.17) give rise to
$c>0$
, this and (10.17) give rise to
for any
![]() $\unicode[STIX]{x1D6FF}$
satisfying
$\unicode[STIX]{x1D6FF}$
satisfying
![]() $0<\unicode[STIX]{x1D6FF}<\min \{|\unicode[STIX]{x1D6FE}_{-1}|,\unicode[STIX]{x1D6FE}_{1}\}$
. Since
$0<\unicode[STIX]{x1D6FF}<\min \{|\unicode[STIX]{x1D6FE}_{-1}|,\unicode[STIX]{x1D6FE}_{1}\}$
. Since
![]() $\overline{\unicode[STIX]{x1D701}}_{\infty }\not \equiv 0$
, this contradicts to (10.16), if we choose
$\overline{\unicode[STIX]{x1D701}}_{\infty }\not \equiv 0$
, this contradicts to (10.16), if we choose
![]() $0<\unicode[STIX]{x1D6FF}<\min \{|\unicode[STIX]{x1D6FE}_{-1}|,\unicode[STIX]{x1D6FE}_{1}\}$
at the beginning. This finishes the proof of the exponential decay
$0<\unicode[STIX]{x1D6FF}<\min \{|\unicode[STIX]{x1D6FE}_{-1}|,\unicode[STIX]{x1D6FE}_{1}\}$
at the beginning. This finishes the proof of the exponential decay
as
![]() $k\rightarrow \infty$
.
$k\rightarrow \infty$
.
Now we show this indicates the exponential decay of
![]() $\Vert \unicode[STIX]{x1D701}\Vert _{{\mathcal{E}}_{1,\unicode[STIX]{x1D70F}}}$
. Using (10.5) and (10.3), we also derive
$\Vert \unicode[STIX]{x1D701}\Vert _{{\mathcal{E}}_{1,\unicode[STIX]{x1D70F}}}$
. Using (10.5) and (10.3), we also derive
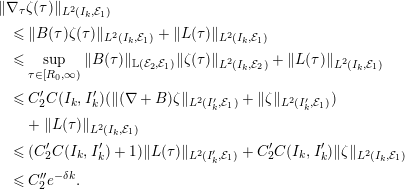 $$\begin{eqnarray}\displaystyle & & \displaystyle \Vert \unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D701}(\unicode[STIX]{x1D70F})\Vert _{L^{2}(I_{k},{\mathcal{E}}_{1})}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \Vert B(\unicode[STIX]{x1D70F})\unicode[STIX]{x1D701}(\unicode[STIX]{x1D70F})\Vert _{L^{2}(I_{k},{\mathcal{E}}_{1})}+\Vert L(\unicode[STIX]{x1D70F})\Vert _{L^{2}(I_{k},{\mathcal{E}}_{1})}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \sup _{\unicode[STIX]{x1D70F}\in [R_{0},\infty )}\Vert B(\unicode[STIX]{x1D70F})\Vert _{\mathbb{L}({\mathcal{E}}_{2},{\mathcal{E}}_{1})}\Vert \unicode[STIX]{x1D701}(\unicode[STIX]{x1D70F})\Vert _{L^{2}(I_{k},{\mathcal{E}}_{2})}+\Vert L(\unicode[STIX]{x1D70F})\Vert _{L^{2}(I_{k},{\mathcal{E}}_{1})}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant C_{2}^{\prime }C(I_{k},I_{k}^{\prime })(\Vert (\unicode[STIX]{x1D6FB}+B)\unicode[STIX]{x1D701}\Vert _{L^{2}(I_{k}^{\prime },{\mathcal{E}}_{1})}+\Vert \unicode[STIX]{x1D701}\Vert _{L^{2}(I_{k}^{\prime },{\mathcal{E}}_{1})})\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\Vert L(\unicode[STIX]{x1D70F})\Vert _{L^{2}(I_{k},{\mathcal{E}}_{1})}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant (C_{2}^{\prime }C(I_{k},I_{k}^{\prime })+1)\Vert L(\unicode[STIX]{x1D70F})\Vert _{L^{2}(I_{k}^{\prime },{\mathcal{E}}_{1})}+C_{2}^{\prime }C(I_{k},I_{k}^{\prime })\Vert \unicode[STIX]{x1D701}\Vert _{L^{2}(I_{k},{\mathcal{E}}_{1})}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant C_{2}^{\prime \prime }e^{-\unicode[STIX]{x1D6FF}k}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \Vert \unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D701}(\unicode[STIX]{x1D70F})\Vert _{L^{2}(I_{k},{\mathcal{E}}_{1})}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \Vert B(\unicode[STIX]{x1D70F})\unicode[STIX]{x1D701}(\unicode[STIX]{x1D70F})\Vert _{L^{2}(I_{k},{\mathcal{E}}_{1})}+\Vert L(\unicode[STIX]{x1D70F})\Vert _{L^{2}(I_{k},{\mathcal{E}}_{1})}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \sup _{\unicode[STIX]{x1D70F}\in [R_{0},\infty )}\Vert B(\unicode[STIX]{x1D70F})\Vert _{\mathbb{L}({\mathcal{E}}_{2},{\mathcal{E}}_{1})}\Vert \unicode[STIX]{x1D701}(\unicode[STIX]{x1D70F})\Vert _{L^{2}(I_{k},{\mathcal{E}}_{2})}+\Vert L(\unicode[STIX]{x1D70F})\Vert _{L^{2}(I_{k},{\mathcal{E}}_{1})}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant C_{2}^{\prime }C(I_{k},I_{k}^{\prime })(\Vert (\unicode[STIX]{x1D6FB}+B)\unicode[STIX]{x1D701}\Vert _{L^{2}(I_{k}^{\prime },{\mathcal{E}}_{1})}+\Vert \unicode[STIX]{x1D701}\Vert _{L^{2}(I_{k}^{\prime },{\mathcal{E}}_{1})})\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\Vert L(\unicode[STIX]{x1D70F})\Vert _{L^{2}(I_{k},{\mathcal{E}}_{1})}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant (C_{2}^{\prime }C(I_{k},I_{k}^{\prime })+1)\Vert L(\unicode[STIX]{x1D70F})\Vert _{L^{2}(I_{k}^{\prime },{\mathcal{E}}_{1})}+C_{2}^{\prime }C(I_{k},I_{k}^{\prime })\Vert \unicode[STIX]{x1D701}\Vert _{L^{2}(I_{k},{\mathcal{E}}_{1})}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant C_{2}^{\prime \prime }e^{-\unicode[STIX]{x1D6FF}k}.\end{eqnarray}$$
Here we have chosen
![]() $I_{k}^{\prime }=[k-1/3,k+4/3]$
,
$I_{k}^{\prime }=[k-1/3,k+4/3]$
,
Combining (10.18) and (10.19), we have derived
![]() $\Vert \unicode[STIX]{x1D701}\Vert _{W^{1,2}(I_{k},{\mathcal{E}}_{1})}\leqslant C_{2}e^{-\unicode[STIX]{x1D6FF}k}$
for all
$\Vert \unicode[STIX]{x1D701}\Vert _{W^{1,2}(I_{k},{\mathcal{E}}_{1})}\leqslant C_{2}e^{-\unicode[STIX]{x1D6FF}k}$
for all
![]() $k$
with
$k$
with
![]() $C_{2}=\max \{C,C_{2}^{\prime \prime }\}$
.
$C_{2}=\max \{C,C_{2}^{\prime \prime }\}$
.
By applying Sobolev’s inequality for the section
![]() $I_{k}\rightarrow {\mathcal{E}}_{1}$
$I_{k}\rightarrow {\mathcal{E}}_{1}$
with
![]() $C_{3}$
the Sobolev constant on
$C_{3}$
the Sobolev constant on
![]() $I_{k}$
. This now finishes the proof.◻
$I_{k}$
. This now finishes the proof.◻
11 Exponential convergence: the prequantization case
To make the main arguments transparent in the scheme of our exponential estimates, we start with the case of prequantization, that is, the case without
![]() ${\mathcal{N}}$
and the normal form contains
${\mathcal{N}}$
and the normal form contains
![]() $E$
only. The general case will be dealt with in the next section.
$E$
only. The general case will be dealt with in the next section.
We put the basic hypothesis that
for all
![]() $\unicode[STIX]{x1D70F}\geqslant \unicode[STIX]{x1D70F}_{0}$
in our further study, where
$\unicode[STIX]{x1D70F}\geqslant \unicode[STIX]{x1D70F}_{0}$
in our further study, where
![]() $\unicode[STIX]{x1D6FF}$
is given as in Proposition 4.8. From Corollary 9.6 and the remark after it, we can locally work with everything in a neighborhood of zero section in the normal form
$\unicode[STIX]{x1D6FF}$
is given as in Proposition 4.8. From Corollary 9.6 and the remark after it, we can locally work with everything in a neighborhood of zero section in the normal form
![]() $(U_{E},f\unicode[STIX]{x1D706}_{E},J)$
.
$(U_{E},f\unicode[STIX]{x1D706}_{E},J)$
.
11.1 Computational preparation
For a smooth function
![]() $h$
, we can express its gradient vector field
$h$
, we can express its gradient vector field
![]() $\operatorname{grad}h$
with respect to the metric
$\operatorname{grad}h$
with respect to the metric
![]() $g_{(\unicode[STIX]{x1D706}_{E},J_{0})}=d\unicode[STIX]{x1D706}_{E}(\cdot ,J_{0}\cdot )+\unicode[STIX]{x1D706}_{E}\otimes \unicode[STIX]{x1D706}_{E}$
in terms of the
$g_{(\unicode[STIX]{x1D706}_{E},J_{0})}=d\unicode[STIX]{x1D706}_{E}(\cdot ,J_{0}\cdot )+\unicode[STIX]{x1D706}_{E}\otimes \unicode[STIX]{x1D706}_{E}$
in terms of the
![]() $\unicode[STIX]{x1D706}_{E}$
-contact Hamiltonian vector field
$\unicode[STIX]{x1D706}_{E}$
-contact Hamiltonian vector field
![]() $X_{h}^{d\unicode[STIX]{x1D706}_{E}}$
and the Reeb vector field
$X_{h}^{d\unicode[STIX]{x1D706}_{E}}$
and the Reeb vector field
![]() $X_{E}$
as
$X_{E}$
as
Note the first term
![]() $-J_{0}X_{h}^{d\unicode[STIX]{x1D706}_{E}}=:\operatorname{grad}h^{\unicode[STIX]{x1D70B}}$
is the
$-J_{0}X_{h}^{d\unicode[STIX]{x1D706}_{E}}=:\operatorname{grad}h^{\unicode[STIX]{x1D70B}}$
is the
![]() $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}_{E}}$
-component of
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}_{E}}$
-component of
![]() $\operatorname{grad}h$
.
$\operatorname{grad}h$
.
Consider the vector field
![]() $Y$
along
$Y$
along
![]() $u$
given by
$u$
given by
![]() $Y(\unicode[STIX]{x1D70F},t):=\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D70F}}^{\unicode[STIX]{x1D70B}}e$
where
$Y(\unicode[STIX]{x1D70F},t):=\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D70F}}^{\unicode[STIX]{x1D70B}}e$
where
![]() $w=(u,e)$
in the coordinates defined in Section 4. The vector field
$w=(u,e)$
in the coordinates defined in Section 4. The vector field
![]() $e_{\unicode[STIX]{x1D70F}}=e(\unicode[STIX]{x1D70F},t)$
as a vector field along
$e_{\unicode[STIX]{x1D70F}}=e(\unicode[STIX]{x1D70F},t)$
as a vector field along
![]() $u(\unicode[STIX]{x1D70F},t)$
is nothing but the map
$u(\unicode[STIX]{x1D70F},t)$
is nothing but the map
![]() $(\unicode[STIX]{x1D70F},t)\mapsto I_{w(\unicode[STIX]{x1D70F},t);u(\unicode[STIX]{x1D70F},t)}(\vec{R}(w(\unicode[STIX]{x1D70F},t)))$
as a section of
$(\unicode[STIX]{x1D70F},t)\mapsto I_{w(\unicode[STIX]{x1D70F},t);u(\unicode[STIX]{x1D70F},t)}(\vec{R}(w(\unicode[STIX]{x1D70F},t)))$
as a section of
![]() $u^{\ast }E$
. In particular
$u^{\ast }E$
. In particular
Obviously,
![]() $I_{w(\unicode[STIX]{x1D70F},t);u(\unicode[STIX]{x1D70F},t)}(\vec{R}(w(\unicode[STIX]{x1D70F},t)))$
is pointwise perpendicular to
$I_{w(\unicode[STIX]{x1D70F},t);u(\unicode[STIX]{x1D70F},t)}(\vec{R}(w(\unicode[STIX]{x1D70F},t)))$
is pointwise perpendicular to
![]() $o_{E}\cong Q$
. In particular,
$o_{E}\cong Q$
. In particular,
where
![]() $e_{\unicode[STIX]{x1D70F}}$
is the vector field along the loop
$e_{\unicode[STIX]{x1D70F}}$
is the vector field along the loop
![]() $u_{\unicode[STIX]{x1D70F}}\subset o_{E}$
and we regard
$u_{\unicode[STIX]{x1D70F}}\subset o_{E}$
and we regard
![]() $(\unicode[STIX]{x1D6F1}_{x(T\cdot )}^{u_{\unicode[STIX]{x1D70F}}})^{-1}e_{\unicode[STIX]{x1D70F}}$
as a vector field along
$(\unicode[STIX]{x1D6F1}_{x(T\cdot )}^{u_{\unicode[STIX]{x1D70F}}})^{-1}e_{\unicode[STIX]{x1D70F}}$
as a vector field along
![]() $z=(x(T\cdot ),o_{x(T\cdot )})$
.
$z=(x(T\cdot ),o_{x(T\cdot )})$
.
For further detailed computations, one needs to decompose the contact-instanton map equation
The second equation does not depend on the choice of endomorphisms
![]() $J$
and becomes
$J$
and becomes
which is equivalent to
On the other hand, by the formula (2.11), the first equation
![]() $\overline{\unicode[STIX]{x2202}}_{J}^{f\unicode[STIX]{x1D706}_{E}}w=0$
becomes
$\overline{\unicode[STIX]{x2202}}_{J}^{f\unicode[STIX]{x1D706}_{E}}w=0$
becomes
where
![]() $(w^{\ast }\unicode[STIX]{x1D706}_{E}\,Y_{dg})^{(0,1)}$
is the
$(w^{\ast }\unicode[STIX]{x1D706}_{E}\,Y_{dg})^{(0,1)}$
is the
![]() $(0,1)$
-part of the one-form
$(0,1)$
-part of the one-form
![]() $w^{\ast }\unicode[STIX]{x1D706}_{E}\,Y_{dg}$
with respect to
$w^{\ast }\unicode[STIX]{x1D706}_{E}\,Y_{dg}$
with respect to
![]() $J_{0}$
.
$J_{0}$
.
In terms of the coordinates, the equation can be rewritten as
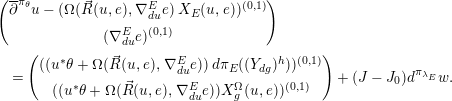 $$\begin{eqnarray}\displaystyle & & \displaystyle \left(\begin{array}{@{}c@{}}\overline{\unicode[STIX]{x2202}}^{\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}}u-(\unicode[STIX]{x1D6FA}(\vec{R}(u,e),\unicode[STIX]{x1D6FB}_{du}^{E}e)\,X_{E}(u,e))^{(0,1)}\\ (\unicode[STIX]{x1D6FB}_{du}^{E}e)^{(0,1)}\end{array}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\begin{array}{@{}c@{}}((u^{\ast }\unicode[STIX]{x1D703}+\unicode[STIX]{x1D6FA}(\vec{R}(u,e),\unicode[STIX]{x1D6FB}_{du}^{E}e))\,d\unicode[STIX]{x1D70B}_{E}((Y_{dg})^{h}))^{(0,1)}\\ ((u^{\ast }\unicode[STIX]{x1D703}+\unicode[STIX]{x1D6FA}(\vec{R}(u,e),\unicode[STIX]{x1D6FB}_{du}^{E}e))X_{g}^{\unicode[STIX]{x1D6FA}}(u,e))^{(0,1)}\end{array}\right)+(J-J_{0})d^{\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}_{E}}}w.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \left(\begin{array}{@{}c@{}}\overline{\unicode[STIX]{x2202}}^{\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}}u-(\unicode[STIX]{x1D6FA}(\vec{R}(u,e),\unicode[STIX]{x1D6FB}_{du}^{E}e)\,X_{E}(u,e))^{(0,1)}\\ (\unicode[STIX]{x1D6FB}_{du}^{E}e)^{(0,1)}\end{array}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\begin{array}{@{}c@{}}((u^{\ast }\unicode[STIX]{x1D703}+\unicode[STIX]{x1D6FA}(\vec{R}(u,e),\unicode[STIX]{x1D6FB}_{du}^{E}e))\,d\unicode[STIX]{x1D70B}_{E}((Y_{dg})^{h}))^{(0,1)}\\ ((u^{\ast }\unicode[STIX]{x1D703}+\unicode[STIX]{x1D6FA}(\vec{R}(u,e),\unicode[STIX]{x1D6FB}_{du}^{E}e))X_{g}^{\unicode[STIX]{x1D6FA}}(u,e))^{(0,1)}\end{array}\right)+(J-J_{0})d^{\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}_{E}}}w.\nonumber\end{eqnarray}$$
Here
![]() $(\unicode[STIX]{x1D6FA}(\vec{R}(u,e),\unicode[STIX]{x1D6FB}_{du}^{E}e)\,X_{E}(u,e))^{(0,1)}$
is the
$(\unicode[STIX]{x1D6FA}(\vec{R}(u,e),\unicode[STIX]{x1D6FB}_{du}^{E}e)\,X_{E}(u,e))^{(0,1)}$
is the
![]() $(0,1)$
-part with respect to
$(0,1)$
-part with respect to
![]() $J_{Q}$
and
$J_{Q}$
and
![]() $(\unicode[STIX]{x1D6FB}_{du}^{E}e)^{(0,1)}$
is the
$(\unicode[STIX]{x1D6FB}_{du}^{E}e)^{(0,1)}$
is the
![]() $(0,1)$
-part with respect to
$(0,1)$
-part with respect to
![]() $J_{E}$
. From this, we have derived
$J_{E}$
. From this, we have derived
Lemma 11.1. In coordinates
![]() $w=(u,e)$
, (11.4) is equivalent to
$w=(u,e)$
, (11.4) is equivalent to
and
with the insertions of
Note that with insertion of (11.10), we obtain
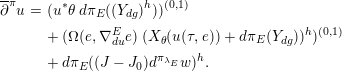 $$\begin{eqnarray}\displaystyle \overline{\unicode[STIX]{x2202}}^{\unicode[STIX]{x1D70B}}u & = & \displaystyle (u^{\ast }\unicode[STIX]{x1D703}\,d\unicode[STIX]{x1D70B}_{E}((Y_{dg})^{h}))^{(0,1)}\nonumber\\ \displaystyle & & \displaystyle +\,(\unicode[STIX]{x1D6FA}(e,\unicode[STIX]{x1D6FB}_{du}^{E}e)\,(X_{\unicode[STIX]{x1D703}}(u(\unicode[STIX]{x1D70F},e))+d\unicode[STIX]{x1D70B}_{E}(Y_{dg}))^{h})^{(0,1)}\nonumber\\ \displaystyle & & \displaystyle +\,d\unicode[STIX]{x1D70B}_{E}((J-J_{0})d^{\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}_{E}}}w)^{h}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \overline{\unicode[STIX]{x2202}}^{\unicode[STIX]{x1D70B}}u & = & \displaystyle (u^{\ast }\unicode[STIX]{x1D703}\,d\unicode[STIX]{x1D70B}_{E}((Y_{dg})^{h}))^{(0,1)}\nonumber\\ \displaystyle & & \displaystyle +\,(\unicode[STIX]{x1D6FA}(e,\unicode[STIX]{x1D6FB}_{du}^{E}e)\,(X_{\unicode[STIX]{x1D703}}(u(\unicode[STIX]{x1D70F},e))+d\unicode[STIX]{x1D70B}_{E}(Y_{dg}))^{h})^{(0,1)}\nonumber\\ \displaystyle & & \displaystyle +\,d\unicode[STIX]{x1D70B}_{E}((J-J_{0})d^{\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}_{E}}}w)^{h}.\end{eqnarray}$$
Now let
![]() $w=(u,e)$
be a contact instanton in terms of the decomposition as above.
$w=(u,e)$
be a contact instanton in terms of the decomposition as above.
Lemma 11.2. Let
![]() $e$
be an arbitrary section over a smooth map
$e$
be an arbitrary section over a smooth map
![]() $u:\unicode[STIX]{x1D6F4}\rightarrow Q$
. Then
$u:\unicode[STIX]{x1D6F4}\rightarrow Q$
. Then
where
![]() $L_{1}(u,e)$
is a
$L_{1}(u,e)$
is a
![]() $(u,e)$
-dependent bilinear map with values in
$(u,e)$
-dependent bilinear map with values in
![]() $\unicode[STIX]{x1D6FA}^{0}(u^{\ast }E)$
and
$\unicode[STIX]{x1D6FA}^{0}(u^{\ast }E)$
and
![]() $L_{2}(u,e)$
is a bilinear map with values in
$L_{2}(u,e)$
is a bilinear map with values in
![]() $\unicode[STIX]{x1D6FA}^{0}(u^{\ast }TQ)$
. They also satisfy
$\unicode[STIX]{x1D6FA}^{0}(u^{\ast }TQ)$
. They also satisfy
An immediate corollary of this lemma is
Corollary 11.3.
 $$\begin{eqnarray}\displaystyle |I_{w;u}(((J-J_{0})d^{\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}_{E}}}w)^{v})| & {\leqslant} & \displaystyle O(1)|e|(|d^{\unicode[STIX]{x1D70B}}u|+|\unicode[STIX]{x1D6FB}e|)\nonumber\\ \displaystyle |\unicode[STIX]{x1D6FB}(I_{w;u}(((J-J_{0})d^{\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}_{E}}}w)^{v}))| & {\leqslant} & \displaystyle O(1)(|du|+|\unicode[STIX]{x1D6FB}e|)^{2}|e|\nonumber\\ \displaystyle & & \displaystyle +\,|\unicode[STIX]{x1D6FB}e|(|du|+|\unicode[STIX]{x1D6FB}e|)+|e||\unicode[STIX]{x1D6FB}^{2}e|).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |I_{w;u}(((J-J_{0})d^{\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}_{E}}}w)^{v})| & {\leqslant} & \displaystyle O(1)|e|(|d^{\unicode[STIX]{x1D70B}}u|+|\unicode[STIX]{x1D6FB}e|)\nonumber\\ \displaystyle |\unicode[STIX]{x1D6FB}(I_{w;u}(((J-J_{0})d^{\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}_{E}}}w)^{v}))| & {\leqslant} & \displaystyle O(1)(|du|+|\unicode[STIX]{x1D6FB}e|)^{2}|e|\nonumber\\ \displaystyle & & \displaystyle +\,|\unicode[STIX]{x1D6FB}e|(|du|+|\unicode[STIX]{x1D6FB}e|)+|e||\unicode[STIX]{x1D6FB}^{2}e|).\nonumber\end{eqnarray}$$
Next, we give the following lemmas whose proofs are straightforward from the definition of
![]() $X_{g}^{\unicode[STIX]{x1D6FA}}$
.
$X_{g}^{\unicode[STIX]{x1D6FA}}$
.
Lemma 11.4. Suppose
![]() $d_{C^{0}}(w(\unicode[STIX]{x1D70F},\cdot ),z(\cdot ))\leqslant \unicode[STIX]{x1D704}_{g}$
. Then
$d_{C^{0}}(w(\unicode[STIX]{x1D70F},\cdot ),z(\cdot ))\leqslant \unicode[STIX]{x1D704}_{g}$
. Then
 $$\begin{eqnarray}\displaystyle X_{g}^{\unicode[STIX]{x1D6FA}}(u,e) & = & \displaystyle D^{v}X_{g}^{\unicode[STIX]{x1D6FA}}(u,0)e+M_{1}(u,e)(e,e)\nonumber\\ \displaystyle d\unicode[STIX]{x1D70B}_{E}(Y_{dg}) & = & \displaystyle M_{2}(u,e)(e)\nonumber\\ \displaystyle \unicode[STIX]{x1D6FA}(e,\unicode[STIX]{x1D6FB}_{du}^{E}e)\,X_{g}^{\unicode[STIX]{x1D6FA}}(u,e) & = & \displaystyle N(u,e)(e,\unicode[STIX]{x1D6FB}_{du}e,e)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle X_{g}^{\unicode[STIX]{x1D6FA}}(u,e) & = & \displaystyle D^{v}X_{g}^{\unicode[STIX]{x1D6FA}}(u,0)e+M_{1}(u,e)(e,e)\nonumber\\ \displaystyle d\unicode[STIX]{x1D70B}_{E}(Y_{dg}) & = & \displaystyle M_{2}(u,e)(e)\nonumber\\ \displaystyle \unicode[STIX]{x1D6FA}(e,\unicode[STIX]{x1D6FB}_{du}^{E}e)\,X_{g}^{\unicode[STIX]{x1D6FA}}(u,e) & = & \displaystyle N(u,e)(e,\unicode[STIX]{x1D6FB}_{du}e,e)\nonumber\end{eqnarray}$$
where
![]() $M_{1}(u,e)$
is a smoothly
$M_{1}(u,e)$
is a smoothly
![]() $(u,e)$
-dependent bilinear map on
$(u,e)$
-dependent bilinear map on
![]() $\unicode[STIX]{x1D6FA}^{0}(u^{\ast }E)$
and
$\unicode[STIX]{x1D6FA}^{0}(u^{\ast }E)$
and
![]() $M_{2}:\unicode[STIX]{x1D6FA}^{0}(u^{\ast }E)\rightarrow \unicode[STIX]{x1D6FA}^{0}(u^{\ast }TQ)$
is a linear map,
$M_{2}:\unicode[STIX]{x1D6FA}^{0}(u^{\ast }E)\rightarrow \unicode[STIX]{x1D6FA}^{0}(u^{\ast }TQ)$
is a linear map,
![]() $N(u,e)$
is a
$N(u,e)$
is a
![]() $(u,e)$
-dependent trilinear map on
$(u,e)$
-dependent trilinear map on
![]() $\unicode[STIX]{x1D6FA}^{0}(u^{\ast }E)$
. They also satisfy
$\unicode[STIX]{x1D6FA}^{0}(u^{\ast }E)$
. They also satisfy
Lemma 11.5.
where
![]() $K(u,e)$
is a
$K(u,e)$
is a
![]() $(u,e)$
-dependent linear map from
$(u,e)$
-dependent linear map from
![]() $\unicode[STIX]{x1D6FA}^{0}(u^{\ast }E)$
to
$\unicode[STIX]{x1D6FA}^{0}(u^{\ast }E)$
to
![]() $\unicode[STIX]{x1D6FA}^{0}(u^{\ast }TQ)$
satisfying
$\unicode[STIX]{x1D6FA}^{0}(u^{\ast }TQ)$
satisfying
11.2
 $L^{2}$
-exponential decay of the normal bundle component
$L^{2}$
-exponential decay of the normal bundle component
 $e$
$e$
Combining Lemmas 11.2, 11.4 and 11.5, we can write (11.8) as
By evaluating (11.15) against
![]() $\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}$
, we derive
$\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}$
, we derive
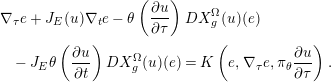 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D70F}}e+J_{E}(u)\unicode[STIX]{x1D6FB}_{t}e-\unicode[STIX]{x1D703}\left(\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}\right)DX_{g}^{\unicode[STIX]{x1D6FA}}(u)(e)\nonumber\\ \displaystyle & & \displaystyle \quad -\,J_{E}\unicode[STIX]{x1D703}\left(\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}t}\right)DX_{g}^{\unicode[STIX]{x1D6FA}}(u)(e)=K\left(e,\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D70F}}e,\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D70F}}e+J_{E}(u)\unicode[STIX]{x1D6FB}_{t}e-\unicode[STIX]{x1D703}\left(\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}\right)DX_{g}^{\unicode[STIX]{x1D6FA}}(u)(e)\nonumber\\ \displaystyle & & \displaystyle \quad -\,J_{E}\unicode[STIX]{x1D703}\left(\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}t}\right)DX_{g}^{\unicode[STIX]{x1D6FA}}(u)(e)=K\left(e,\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D70F}}e,\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}\right).\end{eqnarray}$$
First notice that
Lemma 11.6.
Proof. We consider (11.16) as an equation for
![]() $e$
. Clearly this is a quasilinear elliptic equation of
$e$
. Clearly this is a quasilinear elliptic equation of
![]() $e$
when
$e$
when
![]() $u$
is fixed. We also recall
$u$
is fixed. We also recall
![]() $K(e,\unicode[STIX]{x1D6FB}_{du}e,du)$
has the form
$K(e,\unicode[STIX]{x1D6FB}_{du}e,du)$
has the form
where
![]() $L_{1}(u,e)$
is a bilinear map with
$L_{1}(u,e)$
is a bilinear map with
![]() $|L_{1}(u,e)|=O(1)$
by (11.12) which satisfies the inequality
$|L_{1}(u,e)|=O(1)$
by (11.12) which satisfies the inequality
(See Corollary 11.3.) Now the lemma immediately follows from the convergence
![]() $|\unicode[STIX]{x1D70B}(\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F})|$
,
$|\unicode[STIX]{x1D70B}(\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F})|$
,
![]() $|\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D70F}}e|\rightarrow 0$
established in Corollary 9.6.◻
$|\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D70F}}e|\rightarrow 0$
established in Corollary 9.6.◻
Denote by
![]() $B(\unicode[STIX]{x1D70F})$
a
$B(\unicode[STIX]{x1D70F})$
a
![]() $\unicode[STIX]{x1D70F}$
-family of operators
$\unicode[STIX]{x1D70F}$
-family of operators
defined by
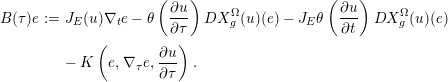 $$\begin{eqnarray}\displaystyle B(\unicode[STIX]{x1D70F})e & := & \displaystyle J_{E}(u)\unicode[STIX]{x1D6FB}_{t}e-\unicode[STIX]{x1D703}\left(\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}\right)DX_{g}^{\unicode[STIX]{x1D6FA}}(u)(e)-J_{E}\unicode[STIX]{x1D703}\left(\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}t}\right)DX_{g}^{\unicode[STIX]{x1D6FA}}(u)(e)\nonumber\\ \displaystyle & & \displaystyle -\,K\left(e,\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D70F}}e,\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}\right).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle B(\unicode[STIX]{x1D70F})e & := & \displaystyle J_{E}(u)\unicode[STIX]{x1D6FB}_{t}e-\unicode[STIX]{x1D703}\left(\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}\right)DX_{g}^{\unicode[STIX]{x1D6FA}}(u)(e)-J_{E}\unicode[STIX]{x1D703}\left(\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}t}\right)DX_{g}^{\unicode[STIX]{x1D6FA}}(u)(e)\nonumber\\ \displaystyle & & \displaystyle -\,K\left(e,\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D70F}}e,\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}\right).\nonumber\end{eqnarray}$$
Then (11.16) for
![]() $e$
with
$e$
with
![]() $u$
fixed can be rewritten as
$u$
fixed can be rewritten as
Once we know
![]() $u(\unicode[STIX]{x1D70F},\cdot )\rightarrow z_{\infty }$
as
$u(\unicode[STIX]{x1D70F},\cdot )\rightarrow z_{\infty }$
as
![]() $\unicode[STIX]{x1D70F}\rightarrow \infty$
for some Reeb orbit
$\unicode[STIX]{x1D70F}\rightarrow \infty$
for some Reeb orbit
![]() $z_{\infty }$
, we can use the exponential map from
$z_{\infty }$
, we can use the exponential map from
![]() $z_{\infty }$
to
$z_{\infty }$
to
![]() $u(\unicode[STIX]{x1D70F},\cdot )$
for any sufficiently large
$u(\unicode[STIX]{x1D70F},\cdot )$
for any sufficiently large
![]() $\unicode[STIX]{x1D70F}$
and its associated parallel transport to regard
$\unicode[STIX]{x1D70F}$
and its associated parallel transport to regard
![]() $B(\unicode[STIX]{x1D70F})$
as a
$B(\unicode[STIX]{x1D70F})$
as a
![]() $\unicode[STIX]{x1D70F}$
-family of linear operators
$\unicode[STIX]{x1D70F}$
-family of linear operators
along the limiting closed Reeb orbit
![]() $z_{\infty }$
. (See [Reference Oh and WangOW2, Section 8] for a detailed discussion on this process.)
$z_{\infty }$
. (See [Reference Oh and WangOW2, Section 8] for a detailed discussion on this process.)
Lemma 11.7. Let
![]() $\unicode[STIX]{x1D70F}_{k}$
be a sequence with
$\unicode[STIX]{x1D70F}_{k}$
be a sequence with
![]() $\unicode[STIX]{x1D70F}_{k}\rightarrow \infty$
, and also denote by
$\unicode[STIX]{x1D70F}_{k}\rightarrow \infty$
, and also denote by
![]() $\unicode[STIX]{x1D70F}_{k}$
a subsequence thereof appearing in Theorem 9.4. Under the abovementioned identification, the operator
$\unicode[STIX]{x1D70F}_{k}$
a subsequence thereof appearing in Theorem 9.4. Under the abovementioned identification, the operator
![]() $B(\unicode[STIX]{x1D70F}_{k})$
converges to the linearized operator
$B(\unicode[STIX]{x1D70F}_{k})$
converges to the linearized operator
as
![]() $k\rightarrow \infty$
.
$k\rightarrow \infty$
.
Proof. Reorganize (11.16) into
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FB}_{\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}e+J_{E}\left(\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}t}e-\unicode[STIX]{x1D706}_{E}\left(\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}t}\right)X_{g}^{\unicode[STIX]{x1D6FA}}(u,e)\right)\nonumber\\ \displaystyle & & \displaystyle \quad -\,\unicode[STIX]{x1D706}_{E}\left(\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}\right)X_{g}^{\unicode[STIX]{x1D6FA}}(u,e)-K\left(e,\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D70F}}e,\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}\right)=0.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FB}_{\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}e+J_{E}\left(\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}t}e-\unicode[STIX]{x1D706}_{E}\left(\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}t}\right)X_{g}^{\unicode[STIX]{x1D6FA}}(u,e)\right)\nonumber\\ \displaystyle & & \displaystyle \quad -\,\unicode[STIX]{x1D706}_{E}\left(\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}\right)X_{g}^{\unicode[STIX]{x1D6FA}}(u,e)-K\left(e,\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D70F}}e,\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}\right)=0.\nonumber\end{eqnarray}$$
We first note that
![]() $\unicode[STIX]{x1D6FB}_{(\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}t)(\unicode[STIX]{x1D70F}_{k},)}\rightarrow {\mathcal{T}}\unicode[STIX]{x1D6FB}_{{\dot{z}}_{\infty }}$
in the operator norm under the above mentioned identification. (See [Reference Oh and WangOW1, Proposition 8.2] and its proof for the precise explanation of this statement.) We now estimate the two terms in the second line. For the first term, we have
$\unicode[STIX]{x1D6FB}_{(\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}t)(\unicode[STIX]{x1D70F}_{k},)}\rightarrow {\mathcal{T}}\unicode[STIX]{x1D6FB}_{{\dot{z}}_{\infty }}$
in the operator norm under the above mentioned identification. (See [Reference Oh and WangOW1, Proposition 8.2] and its proof for the precise explanation of this statement.) We now estimate the two terms in the second line. For the first term, we have
where the last estimate follows from Corollary 9.6 and Lemma 11.3. For the second term, Lemma 11.6 implies that is of order
![]() $o(|e|)$
. This now completes the proof.◻
$o(|e|)$
. This now completes the proof.◻
Note that so far this convergence can only be expected in the subsequence sense. Fortunately this weak convergence is already enough to conduct our scheme of three-interval argument, when combined with the uniform local a priori estimate from [Reference Oh and WangOW2].
Next we briefly explain how the current situation fits into the general framework set up in Section 10. We refer readers to [Reference Oh and WangOW2, Section 8] for further details of this verification.
We first consider two Banach spaces
![]() ${\mathcal{E}}_{1,\unicode[STIX]{x1D70F}}\supset {\mathcal{E}}_{2,\unicode[STIX]{x1D70F}}$
defined by
${\mathcal{E}}_{1,\unicode[STIX]{x1D70F}}\supset {\mathcal{E}}_{2,\unicode[STIX]{x1D70F}}$
defined by
where the maps
are embeddings at
![]() $\unicode[STIX]{x1D70F}\in [0,\infty )$
. This family defines the bundle
$\unicode[STIX]{x1D70F}\in [0,\infty )$
. This family defines the bundle
![]() ${\mathcal{E}}_{i}$
over
${\mathcal{E}}_{i}$
over
![]() $[0,\infty )$
whose fiber at
$[0,\infty )$
whose fiber at
![]() $\unicode[STIX]{x1D70F}$
is given by
$\unicode[STIX]{x1D70F}$
is given by
![]() ${\mathcal{E}}_{1,\unicode[STIX]{x1D70F}}$
: its local triviality can be again proved by the parallel transport over a sufficient small interval
${\mathcal{E}}_{1,\unicode[STIX]{x1D70F}}$
: its local triviality can be again proved by the parallel transport over a sufficient small interval
![]() $(-\unicode[STIX]{x1D700}+\unicode[STIX]{x1D70F},\unicode[STIX]{x1D70F}+\unicode[STIX]{x1D700})$
at each given
$(-\unicode[STIX]{x1D700}+\unicode[STIX]{x1D70F},\unicode[STIX]{x1D70F}+\unicode[STIX]{x1D700})$
at each given
![]() $\unicode[STIX]{x1D70F}\in [0,\infty )$
.
$\unicode[STIX]{x1D70F}\in [0,\infty )$
.
We denote the translation map
![]() $\unicode[STIX]{x1D70E}_{s}(\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D70F}+s$
by
$\unicode[STIX]{x1D70E}_{s}(\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D70F}+s$
by
![]() $\unicode[STIX]{x1D70E}_{s}:[a,b]\rightarrow [0,\infty )$
for each
$\unicode[STIX]{x1D70E}_{s}:[a,b]\rightarrow [0,\infty )$
for each
![]() $s\in [a,b]$
for any given bounded interval
$s\in [a,b]$
for any given bounded interval
![]() $[a,b]\subset [0,\infty )$
. Using the exponential map over the limiting Reeb orbit
$[a,b]\subset [0,\infty )$
. Using the exponential map over the limiting Reeb orbit
![]() $z_{\infty }$
and the associated parallel transport for all sufficiently large
$z_{\infty }$
and the associated parallel transport for all sufficiently large
![]() $k$
’s the sequence of Banach bundles
$k$
’s the sequence of Banach bundles
have global trivializations
The uniform convergence proved in Theorem 9.4 and Corollary 9.6 ensures the uniformly local tameness of
![]() ${\mathcal{E}}_{i}$
and also the precompactness, uniformly local coerciveness of
${\mathcal{E}}_{i}$
and also the precompactness, uniformly local coerciveness of
![]() $B$
. In particular, since
$B$
. In particular, since
uniformly over
![]() $[a,b]$
, we also conclude that the operator
$[a,b]$
, we also conclude that the operator
![]() $B_{\infty }$
defined as
$B_{\infty }$
defined as
is the limit of
![]() $B(\unicode[STIX]{x1D70F})$
for
$B(\unicode[STIX]{x1D70F})$
for
![]() $\unicode[STIX]{x1D70F}\in [a,b]$
with respect to the subsequence
$\unicode[STIX]{x1D70F}\in [a,b]$
with respect to the subsequence
![]() $\{\unicode[STIX]{x1D70F}_{k}\}$
, as shown in Lemma 11.7. Moreover, we also notice that
$\{\unicode[STIX]{x1D70F}_{k}\}$
, as shown in Lemma 11.7. Moreover, we also notice that
![]() $B_{\infty }$
is invariant under the
$B_{\infty }$
is invariant under the
![]() $\unicode[STIX]{x1D70F}$
-translations, and it shows that
$\unicode[STIX]{x1D70F}$
-translations, and it shows that
![]() $B$
is asymptotically cylindrical. Also, it follows from the Morse–Bott condition and Corollary 6.2 that the operator
$B$
is asymptotically cylindrical. Also, it follows from the Morse–Bott condition and Corollary 6.2 that the operator
![]() $B_{\infty }$
is an unbounded self-adjoint operator with trivial kernel. The
$B_{\infty }$
is an unbounded self-adjoint operator with trivial kernel. The
![]() $C^{1}$
-bound of
$C^{1}$
-bound of
![]() $e$
from (11.1) and (9.4) guarantees that the uniform bound of
$e$
from (11.1) and (9.4) guarantees that the uniform bound of
![]() $W^{1,2}(S^{1})$
-norm of
$W^{1,2}(S^{1})$
-norm of
![]() $e(\unicode[STIX]{x1D70F})$
.
$e(\unicode[STIX]{x1D70F})$
.
The above discussion verifies that (11.16) can be fit into the general abstract framework of Theorem 10.11 applied to
![]() $\unicode[STIX]{x1D701}=e$
. Therefore, we immediately obtain the following
$\unicode[STIX]{x1D701}=e$
. Therefore, we immediately obtain the following
![]() $L^{2}$
-exponential estimate.
$L^{2}$
-exponential estimate.
Proposition 11.8. There exists a sufficiently large
![]() $\unicode[STIX]{x1D70F}_{0}>0$
and constants
$\unicode[STIX]{x1D70F}_{0}>0$
and constants
![]() $C_{0}$
,
$C_{0}$
,
![]() $\unicode[STIX]{x1D6FF}_{0}$
such that
$\unicode[STIX]{x1D6FF}_{0}$
such that
for all
![]() $\unicode[STIX]{x1D70F}\geqslant \unicode[STIX]{x1D70F}_{0}$
.
$\unicode[STIX]{x1D70F}\geqslant \unicode[STIX]{x1D70F}_{0}$
.
11.3
 $L^{2}$
-exponential decay of the tangential component
$L^{2}$
-exponential decay of the tangential component
 $du$
I
$du$
I
We summarize previous geometric calculations, especially the equation (11.11), into the following basic equation which we study using the three-interval argument in this section.
Lemma 11.9. We can write the equation (11.11) into the form
so that
![]() $\Vert L(\unicode[STIX]{x1D70F},\cdot )\Vert _{L^{2}(S^{1})}\leqslant Ce^{-\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70F}}$
.
$\Vert L(\unicode[STIX]{x1D70F},\cdot )\Vert _{L^{2}(S^{1})}\leqslant Ce^{-\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70F}}$
.
Proof. We recall
![]() $|du|\leqslant C$
which follows from Corollary 9.6. Furthermore, since
$|du|\leqslant C$
which follows from Corollary 9.6. Furthermore, since
![]() $X_{dg}^{d\unicode[STIX]{x1D706}_{E}}|_{Q}\equiv 0$
, it follows
$X_{dg}^{d\unicode[STIX]{x1D706}_{E}}|_{Q}\equiv 0$
, it follows
Furthermore, by the adaptedness of
![]() $J$
and by the definition of the associated
$J$
and by the definition of the associated
![]() $J_{0}$
, we also have
$J_{0}$
, we also have
![]() $(J-J_{0})|_{Q}\equiv 0$
and so
$(J-J_{0})|_{Q}\equiv 0$
and so
It is manifest that the second term above also carries similar estimate. Combining them, we have established that the right-hand side is bounded by
![]() $C|e|$
from above. Then the required exponential inequality follows from that of
$C|e|$
from above. Then the required exponential inequality follows from that of
![]() $e$
established in Proposition 11.8.◻
$e$
established in Proposition 11.8.◻
In the rest of this section and Section 11.4, we give the proof of the following
Proposition 11.10. There exists some constant
![]() $C_{0}>0$
and
$C_{0}>0$
and
![]() $\unicode[STIX]{x1D6FF}_{0}>0$
such that
$\unicode[STIX]{x1D6FF}_{0}>0$
such that
The proof basically follows the same three-interval argument as in the proof of Theorem 10.11. However, since the current case is much more subtle, we would like to highlight the following points before we start:
(1) unlike the normal component
 $e$
whose governing equation (11.16) is a (inhomogeneous) quasilinear elliptic equation, (11.17) is only (inhomogeneous) quasilinear degenerate elliptic: the limiting operator
$e$
whose governing equation (11.16) is a (inhomogeneous) quasilinear elliptic equation, (11.17) is only (inhomogeneous) quasilinear degenerate elliptic: the limiting operator
 $B$
of its linearization contains nontrivial kernel;
$B$
of its linearization contains nontrivial kernel;(2) nonlinearity of the equation makes somewhat cumbersome to formulate the abstract framework of three-interval argument as in Theorem 10.11 although we believe it is doable. Since this is not the main interest of ours, we directly deal with (11.17) in the present paper postponing such an abstract framework elsewhere in the future;
(3) for the normal component, we directly establish the exponential estimates of the map
 $e$
itself. On the other hand, for the tangential component, partly due to the absence of direct linear structure of
$e$
itself. On the other hand, for the tangential component, partly due to the absence of direct linear structure of
 $u$
and also due to the presence of nontrivial kernel of the asymptotic operator, we prove the exponential decay of the derivative
$u$
and also due to the presence of nontrivial kernel of the asymptotic operator, we prove the exponential decay of the derivative
 $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F})$
first and then prove the exponential convergence to some Reeb orbit afterward;
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F})$
first and then prove the exponential convergence to some Reeb orbit afterward;(4) to obtain the exponential decay of the derivative term, we need to exclude the possibility of a kernel element for the limit obtained in the three-interval argument. In Section 11.4 we use the techniques of the center of mass as an intrinsic geometric coordinates system to exclude the possibility of the vanishing of the limit. This idea appears in [Reference Mundet i Riera and TianMT] and [Reference Oh and ZhuOZ] too;
(5) unlike [Reference Hofer, Wysocki and ZehnderHWZ3] and [Reference BourgeoisBou], our proof directly obtains
 $L^{2}$
-exponential decay instead of showing
$L^{2}$
-exponential decay instead of showing
 $C^{0}$
convergence first and getting exponential decay afterward.
$C^{0}$
convergence first and getting exponential decay afterward.
Starting from now until the end of Section 11.4, we give the proof of Proposition 11.10.
Divide
![]() $[0,\infty )$
into the union of unit intervals
$[0,\infty )$
into the union of unit intervals
![]() $I_{k}=[k,k+1]$
for
$I_{k}=[k,k+1]$
for
![]() $k=0,1,\ldots ,$
and denote by
$k=0,1,\ldots ,$
and denote by
![]() $Z_{k}:=[k,k+1]\times S^{1}$
. In the context below, we also denote by
$Z_{k}:=[k,k+1]\times S^{1}$
. In the context below, we also denote by
![]() $Z^{l}$
the union of three-intervals
$Z^{l}$
the union of three-intervals
![]() $Z_{I}^{l}:=[k,k+1]\times S^{1}$
,
$Z_{I}^{l}:=[k,k+1]\times S^{1}$
,
![]() $Z_{II}^{l}:=[k+1,k+2]\times S^{1}$
and
$Z_{II}^{l}:=[k+1,k+2]\times S^{1}$
and
![]() $Z_{III}^{l}:=[k+2,k+3]\times S^{1}$
.
$Z_{III}^{l}:=[k+2,k+3]\times S^{1}$
.
Consider
![]() $x_{k}:=\Vert \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F})\Vert _{L^{2}(Z_{k})}^{2}$
as symbols in Lemma 10.1. As in the proof of Theorem 10.11, we still use the three-interval inequality as the criterion and consider two situations:
$x_{k}:=\Vert \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F})\Vert _{L^{2}(Z_{k})}^{2}$
as symbols in Lemma 10.1. As in the proof of Theorem 10.11, we still use the three-interval inequality as the criterion and consider two situations:
(1) if there exists some constant
 $\unicode[STIX]{x1D6FF}>0$
such that (11.18)holds for every
$\unicode[STIX]{x1D6FF}>0$
such that (11.18)holds for every $$\begin{eqnarray}\left\Vert \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}\right\Vert _{L^{2}(Z_{k})}^{2}\leqslant \unicode[STIX]{x1D6FE}(2\unicode[STIX]{x1D6FF})\left(\left\Vert \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}\right\Vert _{L^{2}(Z_{k-1})}^{2}+\left\Vert \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}\right\Vert _{L^{2}(Z_{k+1})}^{2}\right)\end{eqnarray}$$
$$\begin{eqnarray}\left\Vert \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}\right\Vert _{L^{2}(Z_{k})}^{2}\leqslant \unicode[STIX]{x1D6FE}(2\unicode[STIX]{x1D6FF})\left(\left\Vert \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}\right\Vert _{L^{2}(Z_{k-1})}^{2}+\left\Vert \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}\right\Vert _{L^{2}(Z_{k+1})}^{2}\right)\end{eqnarray}$$
 $k$
, then from Lemma 10.1, we are done with the proof;
$k$
, then from Lemma 10.1, we are done with the proof;(2) otherwise, we collect all the three-intervals
 $Z^{l_{k}}$
against (11.18), that is, (11.19)In the rest of the proof, we deal with this case.
$Z^{l_{k}}$
against (11.18), that is, (11.19)In the rest of the proof, we deal with this case. $$\begin{eqnarray}\left\Vert \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}\right\Vert _{L^{2}(Z_{II}^{l_{k}})}^{2}>\unicode[STIX]{x1D6FE}(2\unicode[STIX]{x1D6FF})\left(\left\Vert \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}\right\Vert _{L^{2}(Z_{I}^{l_{k}})}^{2}+\left\Vert \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}\right\Vert _{L^{2}(Z_{III}^{l_{k}})}^{2}\right).\end{eqnarray}$$
$$\begin{eqnarray}\left\Vert \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}\right\Vert _{L^{2}(Z_{II}^{l_{k}})}^{2}>\unicode[STIX]{x1D6FE}(2\unicode[STIX]{x1D6FF})\left(\left\Vert \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}\right\Vert _{L^{2}(Z_{I}^{l_{k}})}^{2}+\left\Vert \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}\right\Vert _{L^{2}(Z_{III}^{l_{k}})}^{2}\right).\end{eqnarray}$$
First, if there exists some uniform constant
![]() $C_{1}>0$
such that on each such three-interval
$C_{1}>0$
such that on each such three-interval
then through the same estimates and analysis as for Theorem 10.11, we obtain the exponential decay of
![]() $\Vert \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F})\Vert$
with the presumed rate
$\Vert \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F})\Vert$
with the presumed rate
![]() $\unicode[STIX]{x1D6FF}$
as claimed.
$\unicode[STIX]{x1D6FF}$
as claimed.
Remark 11.11. Here we look at the
![]() $L^{\infty }$
-norm on smaller intervals
$L^{\infty }$
-norm on smaller intervals
![]() $[l_{k}+0.5,l_{k}+2.5]\times S^{1}$
instead of the whole
$[l_{k}+0.5,l_{k}+2.5]\times S^{1}$
instead of the whole
![]() $Z^{l_{k}}=[l_{k},l_{k}+3]\times S^{1}$
is out of consideration for the elliptic bootstrapping argument in Lemma 11.14. However, the change here does not change any argument, since smaller ones are already enough to cover the middle intervals (see Figure 1).
$Z^{l_{k}}=[l_{k},l_{k}+3]\times S^{1}$
is out of consideration for the elliptic bootstrapping argument in Lemma 11.14. However, the change here does not change any argument, since smaller ones are already enough to cover the middle intervals (see Figure 1).
Following the same scheme as for Theorem 10.11, we are going to deal with the case when there is no uniform bound
![]() $C_{1}$
. Then there exists a sequence of constants
$C_{1}$
. Then there exists a sequence of constants
![]() $C_{k}\rightarrow \infty$
and a subsequence of such three-intervals
$C_{k}\rightarrow \infty$
and a subsequence of such three-intervals
![]() $\{Z^{l_{k}}\}$
(still use
$\{Z^{l_{k}}\}$
(still use
![]() $l_{k}$
to denote them) such that
$l_{k}$
to denote them) such that
By Theorem 9.4 and the local uniform
![]() $C^{1}$
-estimate, we can take a subsequence, still denoted by
$C^{1}$
-estimate, we can take a subsequence, still denoted by
![]() $\unicode[STIX]{x1D701}_{k}$
, such that
$\unicode[STIX]{x1D701}_{k}$
, such that
![]() $u(Z^{l_{k}})$
lives in a neighborhood of some closed Reeb orbit
$u(Z^{l_{k}})$
lives in a neighborhood of some closed Reeb orbit
![]() $z_{\infty }$
. Next, we translate the sequence
$z_{\infty }$
. Next, we translate the sequence
![]() $u_{k}:=u|_{Z^{l_{k}}}$
to
$u_{k}:=u|_{Z^{l_{k}}}$
to
![]() $\widetilde{u}_{k}:[0,3]\times S^{1}\rightarrow Q$
by defining
$\widetilde{u}_{k}:[0,3]\times S^{1}\rightarrow Q$
by defining
![]() $\widetilde{u}_{k}(\unicode[STIX]{x1D70F},t)=u_{k}(\unicode[STIX]{x1D70F}+l_{k},t)$
. As before, we also define
$\widetilde{u}_{k}(\unicode[STIX]{x1D70F},t)=u_{k}(\unicode[STIX]{x1D70F}+l_{k},t)$
. As before, we also define
![]() $\widetilde{L}_{k}(\unicode[STIX]{x1D70F},t)=L(\unicode[STIX]{x1D70F}+l_{k},t)$
. From (11.22), we now have
$\widetilde{L}_{k}(\unicode[STIX]{x1D70F},t)=L(\unicode[STIX]{x1D70F}+l_{k},t)$
. From (11.22), we now have
Recalling that
![]() $Q$
carries a natural
$Q$
carries a natural
![]() $S^{1}$
-action induced from the Reeb flow, we equip
$S^{1}$
-action induced from the Reeb flow, we equip
![]() $Q$
with a
$Q$
with a
![]() $S^{1}$
-invariant metric and its associated Levi–Civita connection. In particular, the vector field
$S^{1}$
-invariant metric and its associated Levi–Civita connection. In particular, the vector field
![]() $X_{\unicode[STIX]{x1D706}}$
restricted to
$X_{\unicode[STIX]{x1D706}}$
restricted to
![]() $Q$
is a Killing vector field of the metric and satisfies
$Q$
is a Killing vector field of the metric and satisfies
![]() $\unicode[STIX]{x1D6FB}_{X_{\unicode[STIX]{x1D706}}}X_{\unicode[STIX]{x1D706}}=0$
.
$\unicode[STIX]{x1D6FB}_{X_{\unicode[STIX]{x1D706}}}X_{\unicode[STIX]{x1D706}}=0$
.
Now since the image of
![]() $\widetilde{u}_{k}$
live in neighborhood of a fixed Reeb orbit
$\widetilde{u}_{k}$
live in neighborhood of a fixed Reeb orbit
![]() $z$
in
$z$
in
![]() $Q$
, we can express
$Q$
, we can express
for the normal exponential map
![]() $\exp ^{Z}:NZ\rightarrow Q$
of the locus
$\exp ^{Z}:NZ\rightarrow Q$
of the locus
![]() $Z$
of
$Z$
of
![]() $z$
, where
$z$
, where
![]() $z_{k}(\unicode[STIX]{x1D70F},t)=\unicode[STIX]{x1D70B}_{N}(\widetilde{u}_{k}(\unicode[STIX]{x1D70F},t))$
is the normal projection of
$z_{k}(\unicode[STIX]{x1D70F},t)=\unicode[STIX]{x1D70B}_{N}(\widetilde{u}_{k}(\unicode[STIX]{x1D70F},t))$
is the normal projection of
![]() $\widetilde{u}_{k}(\unicode[STIX]{x1D70F},t)$
to
$\widetilde{u}_{k}(\unicode[STIX]{x1D70F},t)$
to
![]() $Z$
and
$Z$
and
![]() $\unicode[STIX]{x1D701}_{k}(\unicode[STIX]{x1D70F},t)\in N_{z_{k}(\unicode[STIX]{x1D70F},t)}Z=\unicode[STIX]{x1D701}_{z_{k}(\unicode[STIX]{x1D70F},t)}\cap T_{z_{k}(\unicode[STIX]{x1D70F},t)}Q$
. Then
$\unicode[STIX]{x1D701}_{k}(\unicode[STIX]{x1D70F},t)\in N_{z_{k}(\unicode[STIX]{x1D70F},t)}Z=\unicode[STIX]{x1D701}_{z_{k}(\unicode[STIX]{x1D70F},t)}\cap T_{z_{k}(\unicode[STIX]{x1D70F},t)}Q$
. Then
Lemma 11.12.
Proof. To simplify notation, we omit
![]() $k$
here. For each fixed
$k$
here. For each fixed
![]() $(\unicode[STIX]{x1D70F},t)$
, we compute
$(\unicode[STIX]{x1D70F},t)$
, we compute
for a curve
![]() $\unicode[STIX]{x1D6FC}:(-\unicode[STIX]{x1D700},\unicode[STIX]{x1D700})\rightarrow Q$
satisfying
$\unicode[STIX]{x1D6FC}:(-\unicode[STIX]{x1D700},\unicode[STIX]{x1D700})\rightarrow Q$
satisfying
![]() $\unicode[STIX]{x1D6FC}(0)=z(\unicode[STIX]{x1D70F},t)$
,
$\unicode[STIX]{x1D6FC}(0)=z(\unicode[STIX]{x1D70F},t)$
,
![]() $\unicode[STIX]{x1D6FC}^{\prime }(0)=X_{\unicode[STIX]{x1D706}}(z(\unicode[STIX]{x1D70F},t))$
. For example, we can take
$\unicode[STIX]{x1D6FC}^{\prime }(0)=X_{\unicode[STIX]{x1D706}}(z(\unicode[STIX]{x1D70F},t))$
. For example, we can take
![]() $\unicode[STIX]{x1D6FC}(s)=\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D706}}}^{s}(z(\unicode[STIX]{x1D70F},t))$
.
$\unicode[STIX]{x1D6FC}(s)=\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D706}}}^{s}(z(\unicode[STIX]{x1D70F},t))$
.
On the other hand, we compare the initial conditions of the two geodesics
![]() $a\mapsto \exp _{\unicode[STIX]{x1D6FC}(s)}^{Z}a\unicode[STIX]{x1D6F1}_{x}^{\unicode[STIX]{x1D6FC}(s)}(X_{\unicode[STIX]{x1D706}}(x))$
and
$a\mapsto \exp _{\unicode[STIX]{x1D6FC}(s)}^{Z}a\unicode[STIX]{x1D6F1}_{x}^{\unicode[STIX]{x1D6FC}(s)}(X_{\unicode[STIX]{x1D706}}(x))$
and
![]() $a\mapsto \unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D706}}}^{s}(\!\exp _{x}^{Z}a(X_{\unicode[STIX]{x1D706}}(x)))$
with
$a\mapsto \unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D706}}}^{s}(\!\exp _{x}^{Z}a(X_{\unicode[STIX]{x1D706}}(x)))$
with
![]() $x=z(\unicode[STIX]{x1D70F},t)$
. Since
$x=z(\unicode[STIX]{x1D70F},t)$
. Since
![]() $\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D706}}}^{s}$
is an isometry, we derive
$\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D706}}}^{s}$
is an isometry, we derive
Furthermore, we note that
![]() $d\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D706}}}^{s}(X_{\unicode[STIX]{x1D706}}(x))=X_{\unicode[STIX]{x1D706}}(x)$
at
$d\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D706}}}^{s}(X_{\unicode[STIX]{x1D706}}(x))=X_{\unicode[STIX]{x1D706}}(x)$
at
![]() $s=0$
and the field
$s=0$
and the field
![]() $s\mapsto d\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D706}}}^{s}(X_{\unicode[STIX]{x1D706}}(x))$
is parallel along the curve
$s\mapsto d\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D706}}}^{s}(X_{\unicode[STIX]{x1D706}}(x))$
is parallel along the curve
![]() $s\mapsto \unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D706}}}^{s}(x)$
. Therefore by definition of
$s\mapsto \unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D706}}}^{s}(x)$
. Therefore by definition of
![]() $\unicode[STIX]{x1D6F1}_{x}^{\unicode[STIX]{x1D6FC}(s)}(X_{\unicode[STIX]{x1D706}}(z(\unicode[STIX]{x1D70F},t)))$
, we derive
$\unicode[STIX]{x1D6F1}_{x}^{\unicode[STIX]{x1D6FC}(s)}(X_{\unicode[STIX]{x1D706}}(z(\unicode[STIX]{x1D70F},t)))$
, we derive
Combining this discussion, we obtain
for all
![]() $s\in (-\unicode[STIX]{x1D700},\unicode[STIX]{x1D700})$
. Therefore, we obtain
$s\in (-\unicode[STIX]{x1D700},\unicode[STIX]{x1D700})$
. Therefore, we obtain
This shows
![]() $(D_{1}\exp ^{Z})(X_{\unicode[STIX]{x1D706}})=X_{\unicode[STIX]{x1D706}}(\exp _{z(\unicode[STIX]{x1D70F},t)}^{Z}(X_{\unicode[STIX]{x1D706}}(z(\unicode[STIX]{x1D70F},t))))$
.
$(D_{1}\exp ^{Z})(X_{\unicode[STIX]{x1D706}})=X_{\unicode[STIX]{x1D706}}(\exp _{z(\unicode[STIX]{x1D70F},t)}^{Z}(X_{\unicode[STIX]{x1D706}}(z(\unicode[STIX]{x1D70F},t))))$
.
To see
![]() $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}(D_{1}\exp ^{Z})(\unicode[STIX]{x2202}z/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F})=0$
, just note that
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}(D_{1}\exp ^{Z})(\unicode[STIX]{x2202}z/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F})=0$
, just note that
![]() $\unicode[STIX]{x2202}z/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}=k(\unicode[STIX]{x1D70F},t)X_{\unicode[STIX]{x1D706}}(z(\unicode[STIX]{x1D70F},t))$
for some function
$\unicode[STIX]{x2202}z/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}=k(\unicode[STIX]{x1D70F},t)X_{\unicode[STIX]{x1D706}}(z(\unicode[STIX]{x1D70F},t))$
for some function
![]() $k$
, which is parallel to
$k$
, which is parallel to
![]() $X_{\unicode[STIX]{x1D706}}$
and
$X_{\unicode[STIX]{x1D706}}$
and
![]() $z(\unicode[STIX]{x1D70F},t)\in Z$
. Using the definition of
$z(\unicode[STIX]{x1D70F},t)\in Z$
. Using the definition of
![]() $D_{1}\exp ^{Z}(x)(v)$
for
$D_{1}\exp ^{Z}(x)(v)$
for
![]() $v\in T_{x}Q$
at
$v\in T_{x}Q$
at
![]() $x\in Q$
, we compute
$x\in Q$
, we compute
 $$\begin{eqnarray}\displaystyle (D_{1}\exp ^{Z})\left(\frac{\unicode[STIX]{x2202}z}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}\right)(\unicode[STIX]{x1D70F},t) & = & \displaystyle D_{1}\exp ^{Z}(z(\unicode[STIX]{x1D70F},t))(k(\unicode[STIX]{x1D70F},t)X_{\unicode[STIX]{x1D706}}(z(\unicode[STIX]{x1D70F},t)))\nonumber\\ \displaystyle & = & \displaystyle k(\unicode[STIX]{x1D70F},t)D_{1}\exp ^{Z}(z(\unicode[STIX]{x1D70F},t))(X_{\unicode[STIX]{x1D706}}(z(\unicode[STIX]{x1D70F},t))),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (D_{1}\exp ^{Z})\left(\frac{\unicode[STIX]{x2202}z}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}\right)(\unicode[STIX]{x1D70F},t) & = & \displaystyle D_{1}\exp ^{Z}(z(\unicode[STIX]{x1D70F},t))(k(\unicode[STIX]{x1D70F},t)X_{\unicode[STIX]{x1D706}}(z(\unicode[STIX]{x1D70F},t)))\nonumber\\ \displaystyle & = & \displaystyle k(\unicode[STIX]{x1D70F},t)D_{1}\exp ^{Z}(z(\unicode[STIX]{x1D70F},t))(X_{\unicode[STIX]{x1D706}}(z(\unicode[STIX]{x1D70F},t))),\nonumber\end{eqnarray}$$
and hence the
![]() $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}$
projection vanishes.
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}$
projection vanishes.
At last write
and we are done with the first identity claimed.
The second one is proved exactly the same way. ◻
Further noting that
![]() $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}(d_{2}\exp _{z_{k}(\unicode[STIX]{x1D70F},t)}^{Z}):\unicode[STIX]{x1D701}_{z_{k}(\unicode[STIX]{x1D70F},t)}\rightarrow \unicode[STIX]{x1D701}_{z_{k}(\unicode[STIX]{x1D70F},t)}$
is invertible, using this lemma and (11.22), we now have the equation of
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}(d_{2}\exp _{z_{k}(\unicode[STIX]{x1D70F},t)}^{Z}):\unicode[STIX]{x1D701}_{z_{k}(\unicode[STIX]{x1D70F},t)}\rightarrow \unicode[STIX]{x1D701}_{z_{k}(\unicode[STIX]{x1D70F},t)}$
is invertible, using this lemma and (11.22), we now have the equation of
![]() $\unicode[STIX]{x1D701}_{k}$
$\unicode[STIX]{x1D701}_{k}$
where we set
![]() $[\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}(d_{2}\exp )]^{-1}J(\widetilde{u}_{k})[\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}(d_{2}\exp ^{Z})]=:\overline{J}(\unicode[STIX]{x1D70F},t)$
.
$[\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}(d_{2}\exp )]^{-1}J(\widetilde{u}_{k})[\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}(d_{2}\exp ^{Z})]=:\overline{J}(\unicode[STIX]{x1D70F},t)$
.
Next, we rescale this equation by the norm
![]() $\Vert \unicode[STIX]{x1D701}_{k}\Vert _{L^{\infty }([0,3]\times S^{1})}$
:
$\Vert \unicode[STIX]{x1D701}_{k}\Vert _{L^{\infty }([0,3]\times S^{1})}$
:
Lemma 11.13. The norm
![]() $\Vert \unicode[STIX]{x1D701}_{k}\Vert _{L^{\infty }([0,3]\times S^{1})}$
is not zero.
$\Vert \unicode[STIX]{x1D701}_{k}\Vert _{L^{\infty }([0,3]\times S^{1})}$
is not zero.
Proof. Suppose to the contrary that
![]() $\unicode[STIX]{x1D701}_{k}\equiv 0$
. This then implies
$\unicode[STIX]{x1D701}_{k}\equiv 0$
. This then implies
![]() $\widetilde{u}_{k}(\unicode[STIX]{x1D70F},t)\equiv z_{k}(\unicode[STIX]{x1D70F},t)$
for all
$\widetilde{u}_{k}(\unicode[STIX]{x1D70F},t)\equiv z_{k}(\unicode[STIX]{x1D70F},t)$
for all
![]() $(\unicode[STIX]{x1D70F},t)\in [0,3]\times S^{1}$
. Therefore,
$(\unicode[STIX]{x1D70F},t)\in [0,3]\times S^{1}$
. Therefore,
![]() $\unicode[STIX]{x2202}\widetilde{u}_{k}/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}$
is parallel to
$\unicode[STIX]{x2202}\widetilde{u}_{k}/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}$
is parallel to
![]() $X_{\unicode[STIX]{x1D703}}$
on
$X_{\unicode[STIX]{x1D703}}$
on
![]() $[0,3]\times S^{1}$
. In particular
$[0,3]\times S^{1}$
. In particular
![]() $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x2202}\widetilde{u}_{k}/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F})\equiv 0$
. This violates the inequality
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x2202}\widetilde{u}_{k}/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F})\equiv 0$
. This violates the inequality
Therefore, the lemma holds. ◻
Now the rescaled sequence
![]() $\overline{\unicode[STIX]{x1D701}}_{k}:=\unicode[STIX]{x1D701}_{k}/\Vert \unicode[STIX]{x1D701}_{k}\Vert _{L^{\infty }([0,3]\times S^{1})}$
satisfies
$\overline{\unicode[STIX]{x1D701}}_{k}:=\unicode[STIX]{x1D701}_{k}/\Vert \unicode[STIX]{x1D701}_{k}\Vert _{L^{\infty }([0,3]\times S^{1})}$
satisfies
and
The next step is to focus on the right-hand side of (11.26).
Lemma 11.14. The right-hand side of (11.26) converges to zero as
![]() $k\rightarrow \infty$
.
$k\rightarrow \infty$
.
Proof. Since the left-hand side of (11.25) is an elliptic (Cauchy–Riemann type) operator, we have the elliptic estimates
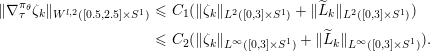 $$\begin{eqnarray}\displaystyle \Vert \unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D70F}}^{\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}}\unicode[STIX]{x1D701}_{k}\Vert _{W^{l,2}([0.5,2.5]\times S^{1})} & {\leqslant} & \displaystyle C_{1}(\Vert \unicode[STIX]{x1D701}_{k}\Vert _{L^{2}([0,3]\times S^{1})}+\Vert \widetilde{L}_{k}\Vert _{L^{2}([0,3]\times S^{1})})\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C_{2}(\Vert \unicode[STIX]{x1D701}_{k}\Vert _{L^{\infty }([0,3]\times S^{1})}+\Vert \widetilde{L}_{k}\Vert _{L^{\infty }([0,3]\times S^{1})}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \Vert \unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D70F}}^{\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}}\unicode[STIX]{x1D701}_{k}\Vert _{W^{l,2}([0.5,2.5]\times S^{1})} & {\leqslant} & \displaystyle C_{1}(\Vert \unicode[STIX]{x1D701}_{k}\Vert _{L^{2}([0,3]\times S^{1})}+\Vert \widetilde{L}_{k}\Vert _{L^{2}([0,3]\times S^{1})})\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C_{2}(\Vert \unicode[STIX]{x1D701}_{k}\Vert _{L^{\infty }([0,3]\times S^{1})}+\Vert \widetilde{L}_{k}\Vert _{L^{\infty }([0,3]\times S^{1})}).\nonumber\end{eqnarray}$$
The Sobolev’s embedding theorem further gives
Hence we have
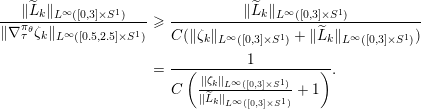 $$\begin{eqnarray}\displaystyle \frac{\Vert \widetilde{L}_{k}\Vert _{L^{\infty }([0,3]\times S^{1})}}{\Vert \unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D70F}}^{\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}}\unicode[STIX]{x1D701}_{k}\Vert _{L^{\infty }([0.5,2.5]\times S^{1})}} & {\geqslant} & \displaystyle \frac{\Vert \widetilde{L}_{k}\Vert _{L^{\infty }([0,3]\times S^{1})}}{C(\Vert \unicode[STIX]{x1D701}_{k}\Vert _{L^{\infty }([0,3]\times S^{1})}+\Vert \widetilde{L}_{k}\Vert _{L^{\infty }([0,3]\times S^{1})})}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{C\left(\frac{\Vert \unicode[STIX]{x1D701}_{k}\Vert _{L^{\infty }([0,3]\times S^{1})}}{\Vert \widetilde{L}_{k}\Vert _{L^{\infty }([0,3]\times S^{1})}}+1\right)}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\Vert \widetilde{L}_{k}\Vert _{L^{\infty }([0,3]\times S^{1})}}{\Vert \unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D70F}}^{\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}}\unicode[STIX]{x1D701}_{k}\Vert _{L^{\infty }([0.5,2.5]\times S^{1})}} & {\geqslant} & \displaystyle \frac{\Vert \widetilde{L}_{k}\Vert _{L^{\infty }([0,3]\times S^{1})}}{C(\Vert \unicode[STIX]{x1D701}_{k}\Vert _{L^{\infty }([0,3]\times S^{1})}+\Vert \widetilde{L}_{k}\Vert _{L^{\infty }([0,3]\times S^{1})})}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{C\left(\frac{\Vert \unicode[STIX]{x1D701}_{k}\Vert _{L^{\infty }([0,3]\times S^{1})}}{\Vert \widetilde{L}_{k}\Vert _{L^{\infty }([0,3]\times S^{1})}}+1\right)}.\nonumber\end{eqnarray}$$
We use our standing assumption (11.21) with
![]() $C_{k}\rightarrow \infty$
as
$C_{k}\rightarrow \infty$
as
![]() $k\rightarrow \infty$
and Lemma 11.12, the left- hand side converges to zero as
$k\rightarrow \infty$
and Lemma 11.12, the left- hand side converges to zero as
![]() $k\rightarrow \infty$
, so we get
$k\rightarrow \infty$
, so we get
Thus the right-hand side of (11.26) converges to zero.◻
Then with the same argument as in the proof of Theorem 10.11, after taking a subsequence, we obtain a limiting section
![]() $\overline{\unicode[STIX]{x1D701}}_{\infty }$
of
$\overline{\unicode[STIX]{x1D701}}_{\infty }$
of
![]() $z_{\infty }^{\ast }\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D703}}$
satisfying
$z_{\infty }^{\ast }\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D703}}$
satisfying
Here to make it compatible with the notation used in Theorem 10.11, we denote by
![]() $B_{\infty }$
the limit operator of
$B_{\infty }$
the limit operator of
![]() $B:=\overline{J}(\unicode[STIX]{x1D70F},t)\unicode[STIX]{x1D6FB}_{t}^{\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}}$
. When applied to horizontal part as in the current case of study, the operator is nothing but the linearization of Reeb orbit
$B:=\overline{J}(\unicode[STIX]{x1D70F},t)\unicode[STIX]{x1D6FB}_{t}^{\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}}$
. When applied to horizontal part as in the current case of study, the operator is nothing but the linearization of Reeb orbit
![]() $z_{\infty }$
followed by action of
$z_{\infty }$
followed by action of
![]() $J$
.
$J$
.
Write
where
![]() $\{e_{i}\}$
is the basis consisting of the eigenfunctions associated to the eigenvalue
$\{e_{i}\}$
is the basis consisting of the eigenfunctions associated to the eigenvalue
![]() $\unicode[STIX]{x1D706}_{i}$
for
$\unicode[STIX]{x1D706}_{i}$
for
![]() $j\geqslant k+1$
with
$j\geqslant k+1$
with
and
![]() $e_{j}$
for
$e_{j}$
for
![]() $j=1,\ldots ,k$
are eigenfunctions of eigenvalue zero. By plugging
$j=1,\ldots ,k$
are eigenfunctions of eigenvalue zero. By plugging
![]() $\overline{\unicode[STIX]{x1D701}}_{\infty }$
into (10.15), we derive
$\overline{\unicode[STIX]{x1D701}}_{\infty }$
into (10.15), we derive
and it follows that
By the same calculation in the proof of Theorem 10.11, it follows
As a conclusion of this section, it remains to show
Lemma 11.15.
This lemma will then lead to contradiction and hence finish the proof of Proposition 11.10. The proof of this nonvanishing is given in the next section via the study of the center of mass.
11.4
 $L^{2}$
-exponential decay of the tangential component
$L^{2}$
-exponential decay of the tangential component
 $du$
II: study of center of mass
$du$
II: study of center of mass
We equip the submanifold with an
![]() $S^{1}$
-invariant metric. Then its associated Levi–Civita connection
$S^{1}$
-invariant metric. Then its associated Levi–Civita connection
![]() $\unicode[STIX]{x1D6FB}$
is also
$\unicode[STIX]{x1D6FB}$
is also
![]() $S^{1}$
-invariant. Denote by
$S^{1}$
-invariant. Denote by
![]() $\exp :U_{o_{Q}}\subset TQ\rightarrow Q\times Q$
the exponential map, and this defines a diffeomorphism between the open neighborhood
$\exp :U_{o_{Q}}\subset TQ\rightarrow Q\times Q$
the exponential map, and this defines a diffeomorphism between the open neighborhood
![]() $U_{o_{Q}}$
of the zero section
$U_{o_{Q}}$
of the zero section
![]() $o_{Q}$
of
$o_{Q}$
of
![]() $TQ$
and some open neighborhood
$TQ$
and some open neighborhood
![]() $U_{\unicode[STIX]{x1D6E5}}$
of the diagonal
$U_{\unicode[STIX]{x1D6E5}}$
of the diagonal
![]() $\unicode[STIX]{x1D6E5}\subset Q\times Q$
. Denote its inverse by
$\unicode[STIX]{x1D6E5}\subset Q\times Q$
. Denote its inverse by
We refer readers to [Reference KarcherK] for the detailed study of the various basic derivative estimates of this map.
The following lemma is a variation of the well-known center of mass techniques from Riemannian geometry with the contact structure being taken into consideration (by introducing the reparameterization function
![]() $h$
in the following statement).
$h$
in the following statement).
Lemma 11.16. Let
![]() $(Q,\unicode[STIX]{x1D703}=\unicode[STIX]{x1D706}|_{Q})$
be the submanifold foliated by closed Reeb orbits of period
$(Q,\unicode[STIX]{x1D703}=\unicode[STIX]{x1D706}|_{Q})$
be the submanifold foliated by closed Reeb orbits of period
![]() $T$
. Then there exists some
$T$
. Then there exists some
![]() $\unicode[STIX]{x1D6FF}>0$
depending only on
$\unicode[STIX]{x1D6FF}>0$
depending only on
![]() $(Q,\unicode[STIX]{x1D703})$
such that for any
$(Q,\unicode[STIX]{x1D703})$
such that for any
![]() $C^{k+1}$
loop
$C^{k+1}$
loop
![]() $\unicode[STIX]{x1D6FE}:S^{1}\rightarrow M$
with
$\unicode[STIX]{x1D6FE}:S^{1}\rightarrow M$
with
![]() $d_{C^{k+1}}(\unicode[STIX]{x1D6FE},\mathfrak{Reeb}(Q,\unicode[STIX]{x1D703}))$
$d_{C^{k+1}}(\unicode[STIX]{x1D6FE},\mathfrak{Reeb}(Q,\unicode[STIX]{x1D703}))$
![]() ${<}\unicode[STIX]{x1D6FF}$
, there exists a unique point
${<}\unicode[STIX]{x1D6FF}$
, there exists a unique point
![]() $m(\unicode[STIX]{x1D6FE})\in Q$
, and a reparameterization map
$m(\unicode[STIX]{x1D6FE})\in Q$
, and a reparameterization map
![]() $h:S^{1}\rightarrow S^{1}$
which is
$h:S^{1}\rightarrow S^{1}$
which is
![]() $C^{k}$
close to
$C^{k}$
close to
![]() $\operatorname{id}_{S^{1}}$
, such that
$\operatorname{id}_{S^{1}}$
, such that
Proof. Consider the functional
defined as
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6F6}(h,m,\unicode[STIX]{x1D6FE})\nonumber\\ \displaystyle & & \displaystyle \quad :=\left(\left(m,\int _{S^{1}}E(m,(\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D703}}}^{Th(t)})^{-1}(\unicode[STIX]{x1D6FE}(t))\,dt)\right)\!,\unicode[STIX]{x1D703}(E(m,(\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D703}}}^{Th(t)})^{-1}(\unicode[STIX]{x1D6FE}(t))))\right)\!,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6F6}(h,m,\unicode[STIX]{x1D6FE})\nonumber\\ \displaystyle & & \displaystyle \quad :=\left(\left(m,\int _{S^{1}}E(m,(\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D703}}}^{Th(t)})^{-1}(\unicode[STIX]{x1D6FE}(t))\,dt)\right)\!,\unicode[STIX]{x1D703}(E(m,(\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D703}}}^{Th(t)})^{-1}(\unicode[STIX]{x1D6FE}(t))))\right)\!,\nonumber\end{eqnarray}$$
where
![]() ${\mathcal{R}}$
denotes the trivial bundle over
${\mathcal{R}}$
denotes the trivial bundle over
![]() $\mathbb{R}\times Q$
over
$\mathbb{R}\times Q$
over
![]() $Q$
.
$Q$
.
If
![]() $\unicode[STIX]{x1D6FE}$
is a Reeb orbit with period
$\unicode[STIX]{x1D6FE}$
is a Reeb orbit with period
![]() $T$
, then
$T$
, then
![]() $h=\operatorname{id}_{S^{1}}$
and
$h=\operatorname{id}_{S^{1}}$
and
![]() $m(\unicode[STIX]{x1D6FE})=\unicode[STIX]{x1D6FE}(0)$
will solve the equation
$m(\unicode[STIX]{x1D6FE})=\unicode[STIX]{x1D6FE}(0)$
will solve the equation
From straightforward calculations
 $$\begin{eqnarray}\displaystyle & & \displaystyle D_{h}\unicode[STIX]{x1D6F6}|_{(\operatorname{id}_{S^{1}},\unicode[STIX]{x1D6FE}(0),\unicode[STIX]{x1D6FE})}(\unicode[STIX]{x1D702})\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\left(m,\int _{S^{1}}d_{2}E|_{(\unicode[STIX]{x1D6FE}(0),\unicode[STIX]{x1D6FE}(0))}(\unicode[STIX]{x1D702}(t)TX_{\unicode[STIX]{x1D703}})\,dt\right)\!,\unicode[STIX]{x1D703}(d_{2}E|_{(\unicode[STIX]{x1D6FE}(0),\unicode[STIX]{x1D6FE}(0))}(\unicode[STIX]{x1D702}(t)TX_{\unicode[STIX]{x1D703}}))\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\left(m,\left(T\int _{S^{1}}\unicode[STIX]{x1D702}(t)\,dt\right)\cdot X_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D6FE}(0))\right)\!,T\unicode[STIX]{x1D702}(t)\right)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle D_{h}\unicode[STIX]{x1D6F6}|_{(\operatorname{id}_{S^{1}},\unicode[STIX]{x1D6FE}(0),\unicode[STIX]{x1D6FE})}(\unicode[STIX]{x1D702})\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\left(m,\int _{S^{1}}d_{2}E|_{(\unicode[STIX]{x1D6FE}(0),\unicode[STIX]{x1D6FE}(0))}(\unicode[STIX]{x1D702}(t)TX_{\unicode[STIX]{x1D703}})\,dt\right)\!,\unicode[STIX]{x1D703}(d_{2}E|_{(\unicode[STIX]{x1D6FE}(0),\unicode[STIX]{x1D6FE}(0))}(\unicode[STIX]{x1D702}(t)TX_{\unicode[STIX]{x1D703}}))\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\left(m,\left(T\int _{S^{1}}\unicode[STIX]{x1D702}(t)\,dt\right)\cdot X_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D6FE}(0))\right)\!,T\unicode[STIX]{x1D702}(t)\right)\nonumber\end{eqnarray}$$
and
 $$\begin{eqnarray}\displaystyle & & \displaystyle D_{m}\unicode[STIX]{x1D6F6}|_{(\operatorname{id}_{S^{1}},\unicode[STIX]{x1D6FE}(0),\unicode[STIX]{x1D6FE})}(v)\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\left(v,\int _{S^{1}}D_{1}E|_{(\unicode[STIX]{x1D6FE}(0),\unicode[STIX]{x1D6FE}(0))}(v)\,dt\right)\!,\unicode[STIX]{x1D703}(D_{1}E|_{(\unicode[STIX]{x1D6FE}(0),\unicode[STIX]{x1D6FE}(0))}(v))\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\left(v,\int _{S^{1}}D_{1}E|_{(\unicode[STIX]{x1D6FE}(0),\unicode[STIX]{x1D6FE}(0))}(v)\,dt\right)\!,\unicode[STIX]{x1D703}(D_{1}E|_{(\unicode[STIX]{x1D6FE}(0),\unicode[STIX]{x1D6FE}(0))}(v))\right)\nonumber\\ \displaystyle & & \displaystyle \quad =((v,v),\unicode[STIX]{x1D703}(v)),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle D_{m}\unicode[STIX]{x1D6F6}|_{(\operatorname{id}_{S^{1}},\unicode[STIX]{x1D6FE}(0),\unicode[STIX]{x1D6FE})}(v)\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\left(v,\int _{S^{1}}D_{1}E|_{(\unicode[STIX]{x1D6FE}(0),\unicode[STIX]{x1D6FE}(0))}(v)\,dt\right)\!,\unicode[STIX]{x1D703}(D_{1}E|_{(\unicode[STIX]{x1D6FE}(0),\unicode[STIX]{x1D6FE}(0))}(v))\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\left(v,\int _{S^{1}}D_{1}E|_{(\unicode[STIX]{x1D6FE}(0),\unicode[STIX]{x1D6FE}(0))}(v)\,dt\right)\!,\unicode[STIX]{x1D703}(D_{1}E|_{(\unicode[STIX]{x1D6FE}(0),\unicode[STIX]{x1D6FE}(0))}(v))\right)\nonumber\\ \displaystyle & & \displaystyle \quad =((v,v),\unicode[STIX]{x1D703}(v)),\nonumber\end{eqnarray}$$
we claim that
![]() $D_{(h,m)}\unicode[STIX]{x1D6F6}$
is transversal to
$D_{(h,m)}\unicode[STIX]{x1D6F6}$
is transversal to
![]() $o_{TM}\times o_{{\mathcal{R}}}$
at the point
$o_{TM}\times o_{{\mathcal{R}}}$
at the point
![]() $(\operatorname{id}_{S^{1}},\unicode[STIX]{x1D6FE}(0),\unicode[STIX]{x1D6FE}(t))$
, where
$(\operatorname{id}_{S^{1}},\unicode[STIX]{x1D6FE}(0),\unicode[STIX]{x1D6FE}(t))$
, where
![]() $\unicode[STIX]{x1D6FE}$
is a Reeb orbit of period
$\unicode[STIX]{x1D6FE}$
is a Reeb orbit of period
![]() $T$
. To see this, notice that for any point in the set
$T$
. To see this, notice that for any point in the set
one can always find its preimage as follows: for any given
![]() $(aX_{\unicode[STIX]{x1D703}}+\unicode[STIX]{x1D707},f)\in TQ\times C^{\infty }(S^{1},\mathbb{R})$
with
$(aX_{\unicode[STIX]{x1D703}}+\unicode[STIX]{x1D707},f)\in TQ\times C^{\infty }(S^{1},\mathbb{R})$
with
![]() $a=\int _{S^{1}}f(t)\,dt$
, the pair
$a=\int _{S^{1}}f(t)\,dt$
, the pair
 $$\begin{eqnarray}\displaystyle v & = & \displaystyle a\cdot X_{\unicode[STIX]{x1D703}}+\unicode[STIX]{x1D707}\nonumber\\ \displaystyle \unicode[STIX]{x1D702}(t) & = & \displaystyle \frac{1}{T}(f(t)-a)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle v & = & \displaystyle a\cdot X_{\unicode[STIX]{x1D703}}+\unicode[STIX]{x1D707}\nonumber\\ \displaystyle \unicode[STIX]{x1D702}(t) & = & \displaystyle \frac{1}{T}(f(t)-a)\nonumber\end{eqnarray}$$
lives in the preimage. This proves surjectivity of the partial derivative
![]() $D_{(h,m)}\unicode[STIX]{x1D6F6}|_{(\operatorname{id}_{S^{1}},\unicode[STIX]{x1D6FE}(0),\unicode[STIX]{x1D6FE})}$
. Then applying the implicit function theorem, we have finished the proof.◻
$D_{(h,m)}\unicode[STIX]{x1D6F6}|_{(\operatorname{id}_{S^{1}},\unicode[STIX]{x1D6FE}(0),\unicode[STIX]{x1D6FE})}$
. Then applying the implicit function theorem, we have finished the proof.◻
Using the center of mass, we can derive the following proposition which will be used to exclude the possibility of the vanishing of
![]() $\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D70F}}^{\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}}\overline{\unicode[STIX]{x1D701}}_{\infty }$
.
$\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D70F}}^{\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}}\overline{\unicode[STIX]{x1D701}}_{\infty }$
.
Proposition 11.17. Recall the rescaling sequence
![]() $\widetilde{\unicode[STIX]{x1D701}}_{k}/L_{k}$
we take in the proof Proposition 11.10 above, and assume for a subsequence,
$\widetilde{\unicode[STIX]{x1D701}}_{k}/L_{k}$
we take in the proof Proposition 11.10 above, and assume for a subsequence,
in
![]() $L^{2}$
. Then
$L^{2}$
. Then
![]() $\int _{S^{1}}(d\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D703}}}^{Tt})^{-1}(\overline{\unicode[STIX]{x1D701}}_{\infty }(\unicode[STIX]{x1D70F},t))\,dt=0$
where
$\int _{S^{1}}(d\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D703}}}^{Tt})^{-1}(\overline{\unicode[STIX]{x1D701}}_{\infty }(\unicode[STIX]{x1D70F},t))\,dt=0$
where
![]() $(d\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D703}}}^{t})^{-1}(\overline{\unicode[STIX]{x1D701}}_{\infty }(\unicode[STIX]{x1D70F},t))\in T_{z(0)}Q$
.
$(d\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D703}}}^{t})^{-1}(\overline{\unicode[STIX]{x1D701}}_{\infty }(\unicode[STIX]{x1D70F},t))\in T_{z(0)}Q$
.
Proof. By the construction of the center of mass applying to maps
![]() $u_{k}(\unicode[STIX]{x1D70F},\cdot ):S^{1}\rightarrow Q$
for
$u_{k}(\unicode[STIX]{x1D70F},\cdot ):S^{1}\rightarrow Q$
for
![]() $\unicode[STIX]{x1D70F}\in [0,3]$
, we have obtained
$\unicode[STIX]{x1D70F}\in [0,3]$
, we have obtained
If we write
![]() $u_{k}(\unicode[STIX]{x1D70F},t)=\exp _{z_{\infty }(\unicode[STIX]{x1D70F},t)}\unicode[STIX]{x1D701}_{k}(\unicode[STIX]{x1D70F},t)$
where
$u_{k}(\unicode[STIX]{x1D70F},t)=\exp _{z_{\infty }(\unicode[STIX]{x1D70F},t)}\unicode[STIX]{x1D701}_{k}(\unicode[STIX]{x1D70F},t)$
where
![]() $z_{\infty }$
is the limit of
$z_{\infty }$
is the limit of
![]() $z_{k}$
defined in (11.23), it follows that
$z_{k}$
defined in (11.23), it follows that
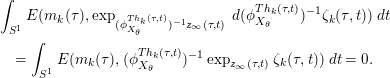 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{S^{1}}E(m_{k}(\unicode[STIX]{x1D70F}),\exp _{(\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D703}}}^{Th_{k}(\unicode[STIX]{x1D70F},t)})^{-1}z_{\infty }(\unicode[STIX]{x1D70F},t)}\,d(\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D703}}}^{Th_{k}(\unicode[STIX]{x1D70F},t)})^{-1}\unicode[STIX]{x1D701}_{k}(\unicode[STIX]{x1D70F},t))\,dt\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{S^{1}}E(m_{k}(\unicode[STIX]{x1D70F}),(\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D703}}}^{Th_{k}(\unicode[STIX]{x1D70F},t)})^{-1}\exp _{z_{\infty }(\unicode[STIX]{x1D70F},t)}\unicode[STIX]{x1D701}_{k}(\unicode[STIX]{x1D70F},t))\,dt=0.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{S^{1}}E(m_{k}(\unicode[STIX]{x1D70F}),\exp _{(\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D703}}}^{Th_{k}(\unicode[STIX]{x1D70F},t)})^{-1}z_{\infty }(\unicode[STIX]{x1D70F},t)}\,d(\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D703}}}^{Th_{k}(\unicode[STIX]{x1D70F},t)})^{-1}\unicode[STIX]{x1D701}_{k}(\unicode[STIX]{x1D70F},t))\,dt\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{S^{1}}E(m_{k}(\unicode[STIX]{x1D70F}),(\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D703}}}^{Th_{k}(\unicode[STIX]{x1D70F},t)})^{-1}\exp _{z_{\infty }(\unicode[STIX]{x1D70F},t)}\unicode[STIX]{x1D701}_{k}(\unicode[STIX]{x1D70F},t))\,dt=0.\end{eqnarray}$$
Recall the following lemma whose proof is direct and we skip.
Lemma 11.18. Let
![]() $\unicode[STIX]{x1D6F1}_{y}^{x}$
is the parallel transport along the short geodesic from
$\unicode[STIX]{x1D6F1}_{y}^{x}$
is the parallel transport along the short geodesic from
![]() $y$
to
$y$
to
![]() $x$
. Then there exists some sufficiently small
$x$
. Then there exists some sufficiently small
![]() $\unicode[STIX]{x1D6FF}>0$
depending only on the given metric on
$\unicode[STIX]{x1D6FF}>0$
depending only on the given metric on
![]() $Q$
and a constant
$Q$
and a constant
![]() $C=C(\unicode[STIX]{x1D6FF})>0$
such that
$C=C(\unicode[STIX]{x1D6FF})>0$
such that
![]() $C(\unicode[STIX]{x1D6FF})\rightarrow 1$
as
$C(\unicode[STIX]{x1D6FF})\rightarrow 1$
as
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
and
$\unicode[STIX]{x1D6FF}\rightarrow 0$
and
In particular
![]() $|E(x,\exp _{y}^{Z}(\cdot ))|\leqslant |\unicode[STIX]{x1D6F1}_{y}^{x}|+C\,d(x,y)$
.
$|E(x,\exp _{y}^{Z}(\cdot ))|\leqslant |\unicode[STIX]{x1D6F1}_{y}^{x}|+C\,d(x,y)$
.
Applying this lemma to (11.31), we obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle \left|\int _{S^{1}}\unicode[STIX]{x1D6F1}_{m_{k}(\unicode[STIX]{x1D70F})}^{(\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D703}}}^{Th_{k}(\unicode[STIX]{x1D70F},t)})^{-1}z_{\infty }(\unicode[STIX]{x1D70F},t)}(d\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D703}}}^{Th(t)})^{-1}\unicode[STIX]{x1D701}_{k}(\unicode[STIX]{x1D70F},t)\,dt\right|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \int _{S^{1}}C\,d(m_{k}(\unicode[STIX]{x1D70F}),(\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D703}}}^{Th_{k}(\unicode[STIX]{x1D70F},t)})^{-1}z_{\infty }(\unicode[STIX]{x1D70F},t))((d\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D703}}}^{Th(t)})^{-1}\unicode[STIX]{x1D701}_{k}(\unicode[STIX]{x1D70F},t))\,dt.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \left|\int _{S^{1}}\unicode[STIX]{x1D6F1}_{m_{k}(\unicode[STIX]{x1D70F})}^{(\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D703}}}^{Th_{k}(\unicode[STIX]{x1D70F},t)})^{-1}z_{\infty }(\unicode[STIX]{x1D70F},t)}(d\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D703}}}^{Th(t)})^{-1}\unicode[STIX]{x1D701}_{k}(\unicode[STIX]{x1D70F},t)\,dt\right|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \int _{S^{1}}C\,d(m_{k}(\unicode[STIX]{x1D70F}),(\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D703}}}^{Th_{k}(\unicode[STIX]{x1D70F},t)})^{-1}z_{\infty }(\unicode[STIX]{x1D70F},t))((d\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D703}}}^{Th(t)})^{-1}\unicode[STIX]{x1D701}_{k}(\unicode[STIX]{x1D70F},t))\,dt.\nonumber\end{eqnarray}$$
We rescale
![]() $\unicode[STIX]{x1D701}_{k}$
by using
$\unicode[STIX]{x1D701}_{k}$
by using
![]() $L_{k}$
and derive that
$L_{k}$
and derive that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \left|\int _{S^{1}}\unicode[STIX]{x1D6F1}_{m_{k}(\unicode[STIX]{x1D70F})}^{(\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D703}}}^{Th_{k}(\unicode[STIX]{x1D70F},t)})^{-1}z_{\infty }(\unicode[STIX]{x1D70F},t)}(d\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D703}}}^{Th_{k}(\unicode[STIX]{x1D70F},t)})^{-1}\frac{\unicode[STIX]{x1D701}_{k}(\unicode[STIX]{x1D70F},t)}{L_{k}}\,dt\right|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \int _{S^{1}}C\,d(m_{k}(\unicode[STIX]{x1D70F}),(\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D703}}}^{Th_{k}(\unicode[STIX]{x1D70F},t)})^{-1}z_{\infty }(\unicode[STIX]{x1D70F},t))\left|(d\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D703}}}^{Th_{k}(\unicode[STIX]{x1D70F},t)})^{-1}\frac{\unicode[STIX]{x1D701}_{k}(\unicode[STIX]{x1D70F},t)}{L_{k}}\right|dt.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \left|\int _{S^{1}}\unicode[STIX]{x1D6F1}_{m_{k}(\unicode[STIX]{x1D70F})}^{(\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D703}}}^{Th_{k}(\unicode[STIX]{x1D70F},t)})^{-1}z_{\infty }(\unicode[STIX]{x1D70F},t)}(d\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D703}}}^{Th_{k}(\unicode[STIX]{x1D70F},t)})^{-1}\frac{\unicode[STIX]{x1D701}_{k}(\unicode[STIX]{x1D70F},t)}{L_{k}}\,dt\right|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \int _{S^{1}}C\,d(m_{k}(\unicode[STIX]{x1D70F}),(\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D703}}}^{Th_{k}(\unicode[STIX]{x1D70F},t)})^{-1}z_{\infty }(\unicode[STIX]{x1D70F},t))\left|(d\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D703}}}^{Th_{k}(\unicode[STIX]{x1D70F},t)})^{-1}\frac{\unicode[STIX]{x1D701}_{k}(\unicode[STIX]{x1D70F},t)}{L_{k}}\right|dt.\nonumber\end{eqnarray}$$
Take
![]() $k\rightarrow \infty$
, and since that
$k\rightarrow \infty$
, and since that
![]() $m_{k}(\unicode[STIX]{x1D70F})\rightarrow z_{\infty }(0)$
and
$m_{k}(\unicode[STIX]{x1D70F})\rightarrow z_{\infty }(0)$
and
![]() $h_{k}\rightarrow \operatorname{id}_{S^{1}}$
uniformly, we get
$h_{k}\rightarrow \operatorname{id}_{S^{1}}$
uniformly, we get
![]() $d(m_{k}(\unicode[STIX]{x1D70F}),(\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D703}}}^{Th_{k}(\unicode[STIX]{x1D70F},t)})^{-1}z_{\infty }(\unicode[STIX]{x1D70F},t))\rightarrow 0$
uniformly over
$d(m_{k}(\unicode[STIX]{x1D70F}),(\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D703}}}^{Th_{k}(\unicode[STIX]{x1D70F},t)})^{-1}z_{\infty }(\unicode[STIX]{x1D70F},t))\rightarrow 0$
uniformly over
![]() $(\unicode[STIX]{x1D70F},t)\in [0,3]\times S^{1}$
as
$(\unicode[STIX]{x1D70F},t)\in [0,3]\times S^{1}$
as
![]() $k\rightarrow \infty$
. Therefore, the right-hand side of this inequality goes to 0. On the other hand by the same reason, we obtain
$k\rightarrow \infty$
. Therefore, the right-hand side of this inequality goes to 0. On the other hand by the same reason, we obtain
uniformly and hence we obtain
![]() $\int _{S^{1}}(d\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D703}}}^{Tt})^{-1}\overline{\unicode[STIX]{x1D701}}_{\infty }\,dt=0$
.◻
$\int _{S^{1}}(d\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D703}}}^{Tt})^{-1}\overline{\unicode[STIX]{x1D701}}_{\infty }\,dt=0$
.◻
Using this proposition, we now prove
![]() $\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D70F}}^{\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}}\overline{\unicode[STIX]{x1D701}}_{\infty }\neq 0$
, which is the last piece of finishing the proof of Proposition 11.10.
$\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D70F}}^{\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}}\overline{\unicode[STIX]{x1D701}}_{\infty }\neq 0$
, which is the last piece of finishing the proof of Proposition 11.10.
Proof of Lemma 11.15.
Suppose to the contrary, that is,
![]() $\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D70F}}^{\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}}\overline{\unicode[STIX]{x1D701}}_{\infty }=0$
, then we would have
$\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D70F}}^{\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}}\overline{\unicode[STIX]{x1D701}}_{\infty }=0$
, then we would have
![]() $J(z_{\infty }(t))\unicode[STIX]{x1D6FB}_{t}\overline{\unicode[STIX]{x1D701}}_{\infty }=0$
from (11.27) and the remark right after it.
$J(z_{\infty }(t))\unicode[STIX]{x1D6FB}_{t}\overline{\unicode[STIX]{x1D701}}_{\infty }=0$
from (11.27) and the remark right after it.
Fix a basis
![]() $\{v_{1},\ldots ,v_{2k}\}$
of
$\{v_{1},\ldots ,v_{2k}\}$
of
![]() $\unicode[STIX]{x1D709}_{z(0)}\subset T_{z(0)}Q$
and define
$\unicode[STIX]{x1D709}_{z(0)}\subset T_{z(0)}Q$
and define
![]() $e_{i}(t)=d\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D703}}}^{t}(v_{i})$
for
$e_{i}(t)=d\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D703}}}^{t}(v_{i})$
for
![]() $i=1,\ldots ,2k$
. Since
$i=1,\ldots ,2k$
. Since
![]() $\unicode[STIX]{x1D6FB}_{t}^{\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}}$
is nothing but the linearization of the Reeb orbit
$\unicode[STIX]{x1D6FB}_{t}^{\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}}$
is nothing but the linearization of the Reeb orbit
![]() $z_{\infty }$
, the Morse–Bott condition implies
$z_{\infty }$
, the Morse–Bott condition implies
![]() $\ker B_{\infty }=\operatorname{span}\{e_{i}(t)\}_{i=1}^{2k}$
. Then one can express
$\ker B_{\infty }=\operatorname{span}\{e_{i}(t)\}_{i=1}^{2k}$
. Then one can express
![]() $\overline{\unicode[STIX]{x1D701}}_{\infty }(t)=\sum _{i=1}^{2k}a_{i}(t)e_{i}(t)$
. Moreover, since
$\overline{\unicode[STIX]{x1D701}}_{\infty }(t)=\sum _{i=1}^{2k}a_{i}(t)e_{i}(t)$
. Moreover, since
![]() $e_{i}$
are parallel (with respect to the
$e_{i}$
are parallel (with respect to the
![]() $S^{1}$
-invariant connection) by construction, it follows
$S^{1}$
-invariant connection) by construction, it follows
![]() $a_{i}$
are constants,
$a_{i}$
are constants,
![]() $i=1,\ldots ,2k$
. Then we can write
$i=1,\ldots ,2k$
. Then we can write
![]() $\overline{\unicode[STIX]{x1D701}}_{\infty }(t)=\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D703}}}^{t}(v)$
, where
$\overline{\unicode[STIX]{x1D701}}_{\infty }(t)=\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D703}}}^{t}(v)$
, where
![]() $v=\sum _{i=1}^{2k}a_{i}v_{i}$
, and further it follows that
$v=\sum _{i=1}^{2k}a_{i}v_{i}$
, and further it follows that
![]() $\int _{S^{1}}(d\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D703}}}^{t})^{-1}(\overline{\unicode[STIX]{x1D701}}_{\infty }(t))\,dt=v$
. On the other hand, from Proposition 11.17,
$\int _{S^{1}}(d\unicode[STIX]{x1D719}_{X_{\unicode[STIX]{x1D703}}}^{t})^{-1}(\overline{\unicode[STIX]{x1D701}}_{\infty }(t))\,dt=v$
. On the other hand, from Proposition 11.17,
![]() $v=0$
and further
$v=0$
and further
![]() $\overline{\unicode[STIX]{x1D701}}_{\infty }\equiv 0$
, which contradicts with
$\overline{\unicode[STIX]{x1D701}}_{\infty }\equiv 0$
, which contradicts with
![]() $\Vert \overline{\unicode[STIX]{x1D701}}_{\infty }\Vert _{L^{\infty }([0,3]\times S^{1})}=1$
.
$\Vert \overline{\unicode[STIX]{x1D701}}_{\infty }\Vert _{L^{\infty }([0,3]\times S^{1})}=1$
.
Thus finally we conclude that
![]() $\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D70F}}^{\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}}\overline{\unicode[STIX]{x1D701}}_{\infty }$
cannot be zero.◻
$\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D70F}}^{\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}}\overline{\unicode[STIX]{x1D701}}_{\infty }$
cannot be zero.◻
This now concludes the proof of Proposition 11.10.
11.5
 $L^{2}$
-exponential decay of the Reeb component of
$L^{2}$
-exponential decay of the Reeb component of
 $dw$
$dw$
We again consider the equation
as an equation for
![]() $e$
. Clearly this is a quasilinear elliptic equation of
$e$
. Clearly this is a quasilinear elliptic equation of
![]() $e$
when
$e$
when
![]() $u$
is fixed. Applying the uniform (local) elliptic estimates to (11.32), the
$u$
is fixed. Applying the uniform (local) elliptic estimates to (11.32), the
![]() $L^{2}$
-exponential decays of
$L^{2}$
-exponential decays of
![]() $e$
and convergence of
$e$
and convergence of
![]() $\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}$
to 0 then lead to the
$\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}$
to 0 then lead to the
![]() $L^{2}$
-exponential decay of
$L^{2}$
-exponential decay of
![]() $\unicode[STIX]{x1D6FB}_{du}e$
. Combining these, we have obtained
$\unicode[STIX]{x1D6FB}_{du}e$
. Combining these, we have obtained
![]() $L^{2}$
-exponential estimates of the
$L^{2}$
-exponential estimates of the
![]() $\unicode[STIX]{x1D70B}\,dw$
.
$\unicode[STIX]{x1D70B}\,dw$
.
Now we consider the original map
![]() $w=(u,e)$
which satisfies (11.4)
$w=(u,e)$
which satisfies (11.4)
where
![]() $\unicode[STIX]{x1D706}=f\unicode[STIX]{x1D706}_{E}$
. We recall that this system is an elliptic system and the corresponding uniform local a priori estimates was established in [Reference Oh and WangOW2]. Then by the elliptic bootstrapping argument using the local uniform a priori estimates on the cylindrical region, we obtain higher-order
$\unicode[STIX]{x1D706}=f\unicode[STIX]{x1D706}_{E}$
. We recall that this system is an elliptic system and the corresponding uniform local a priori estimates was established in [Reference Oh and WangOW2]. Then by the elliptic bootstrapping argument using the local uniform a priori estimates on the cylindrical region, we obtain higher-order
![]() $W^{k,2}$
-exponential decay of
$W^{k,2}$
-exponential decay of
![]() $\unicode[STIX]{x1D70B}\,dw$
for all
$\unicode[STIX]{x1D70B}\,dw$
for all
![]() $k\geqslant 0$
under Hypothesis 9.7.
$k\geqslant 0$
under Hypothesis 9.7.
Next, in the rest of this subsection, we prove the exponential decay of the Reeb component
![]() $w^{\ast }\unicode[STIX]{x1D706}$
. For this purpose, we define a complex-valued function
$w^{\ast }\unicode[STIX]{x1D706}$
. For this purpose, we define a complex-valued function
The following lemma is easy to prove.
Lemma 11.19. Let
![]() $\unicode[STIX]{x1D701}=\unicode[STIX]{x1D70B}(\unicode[STIX]{x2202}w/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F})$
on the cylindrical ends. Then
$\unicode[STIX]{x1D701}=\unicode[STIX]{x1D70B}(\unicode[STIX]{x2202}w/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F})$
on the cylindrical ends. Then
Combining this lemma together with the equation
![]() $d(w^{\ast }\unicode[STIX]{x1D706}\circ j)=0$
, we notice that
$d(w^{\ast }\unicode[STIX]{x1D706}\circ j)=0$
, we notice that
![]() $\unicode[STIX]{x1D6FC}$
satisfies the equations
$\unicode[STIX]{x1D6FC}$
satisfies the equations
where
![]() $\overline{\unicode[STIX]{x2202}}=(1/2)((\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F})+\sqrt{-1}(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}t))$
the standard Cauchy–Riemann operator for the standard complex structure
$\overline{\unicode[STIX]{x2202}}=(1/2)((\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D70F})+\sqrt{-1}(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}t))$
the standard Cauchy–Riemann operator for the standard complex structure
![]() $J_{0}=\sqrt{-1}$
.
$J_{0}=\sqrt{-1}$
.
Notice that from previous section we have already established the
![]() $W^{1,2}$
-exponential decay of
$W^{1,2}$
-exponential decay of
![]() $\unicode[STIX]{x1D708}=(1/2)|\unicode[STIX]{x1D701}|^{2}$
. The exponential decay of
$\unicode[STIX]{x1D708}=(1/2)|\unicode[STIX]{x1D701}|^{2}$
. The exponential decay of
![]() $\unicode[STIX]{x1D6FC}$
follows from the following lemma, whose proof can be proved again by the three-interval method in a much easier way and so omitted.
$\unicode[STIX]{x1D6FC}$
follows from the following lemma, whose proof can be proved again by the three-interval method in a much easier way and so omitted.
Lemma 11.20. Suppose the complex-valued functions
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D708}$
defined on
$\unicode[STIX]{x1D708}$
defined on
![]() $[0,\infty )\times S^{1}$
satisfy
$[0,\infty )\times S^{1}$
satisfy
 $$\begin{eqnarray}\displaystyle \left\{\begin{array}{@{}l@{}}\overline{\unicode[STIX]{x2202}}\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D708}\quad \\ \Vert \unicode[STIX]{x1D708}\Vert _{L^{2}(S^{1})}+\Vert \unicode[STIX]{x1D6FB}\unicode[STIX]{x1D708}\Vert _{L^{2}(S^{1})}\leqslant Ce^{-\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70F}}\quad \text{for some constants}~C,\unicode[STIX]{x1D6FF}>0\quad \\ \lim _{\unicode[STIX]{x1D70F}\rightarrow +\infty }\unicode[STIX]{x1D6FC}=0\quad \end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left\{\begin{array}{@{}l@{}}\overline{\unicode[STIX]{x2202}}\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D708}\quad \\ \Vert \unicode[STIX]{x1D708}\Vert _{L^{2}(S^{1})}+\Vert \unicode[STIX]{x1D6FB}\unicode[STIX]{x1D708}\Vert _{L^{2}(S^{1})}\leqslant Ce^{-\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70F}}\quad \text{for some constants}~C,\unicode[STIX]{x1D6FF}>0\quad \\ \lim _{\unicode[STIX]{x1D70F}\rightarrow +\infty }\unicode[STIX]{x1D6FC}=0\quad \end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
then
![]() $\Vert \unicode[STIX]{x1D6FC}\Vert _{L^{2}(S^{1})}\leqslant \overline{C}e^{-\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70F}}$
for some constant
$\Vert \unicode[STIX]{x1D6FC}\Vert _{L^{2}(S^{1})}\leqslant \overline{C}e^{-\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70F}}$
for some constant
![]() $\overline{C}$
.
$\overline{C}$
.
11.6
 $C^{0}$
exponential convergence
$C^{0}$
exponential convergence
Now we prove
![]() $C^{0}$
-exponential convergence of
$C^{0}$
-exponential convergence of
![]() $w(\unicode[STIX]{x1D70F},\cdot )$
to some Reeb orbit as
$w(\unicode[STIX]{x1D70F},\cdot )$
to some Reeb orbit as
![]() $\unicode[STIX]{x1D70F}\rightarrow \infty$
from the
$\unicode[STIX]{x1D70F}\rightarrow \infty$
from the
![]() $L^{2}$
-exponential estimates presented in previous sections.
$L^{2}$
-exponential estimates presented in previous sections.
Proposition 11.21. Under Hypothesis 9.1, for any contact instanton
![]() $w$
with vanishing charge, there exists a unique Reeb orbit
$w$
with vanishing charge, there exists a unique Reeb orbit
![]() $z(\cdot )=\unicode[STIX]{x1D6FE}(T\cdot ):S^{1}\rightarrow M$
with period
$z(\cdot )=\unicode[STIX]{x1D6FE}(T\cdot ):S^{1}\rightarrow M$
with period
![]() ${\mathcal{T}}>0$
, such that
${\mathcal{T}}>0$
, such that
as
![]() $\unicode[STIX]{x1D70F}\rightarrow +\infty$
, where
$\unicode[STIX]{x1D70F}\rightarrow +\infty$
, where
![]() $d$
denotes the distance on
$d$
denotes the distance on
![]() $M$
defined by the triad metric.
$M$
defined by the triad metric.
Proof. We start with the following lemma
Lemma 11.22. Let
![]() $t\in S^{1}$
be given. Then for any given
$t\in S^{1}$
be given. Then for any given
![]() $\unicode[STIX]{x1D716}>0$
, there exists sufficiently large
$\unicode[STIX]{x1D716}>0$
, there exists sufficiently large
![]() $\unicode[STIX]{x1D70F}_{1}>0$
such that
$\unicode[STIX]{x1D70F}_{1}>0$
such that
for all
![]() $\unicode[STIX]{x1D70F}$
,
$\unicode[STIX]{x1D70F}$
,
![]() $\unicode[STIX]{x1D70F}^{\prime }\geqslant \unicode[STIX]{x1D70F}_{1}$
.
$\unicode[STIX]{x1D70F}^{\prime }\geqslant \unicode[STIX]{x1D70F}_{1}$
.
Proof. Suppose to the contrary that there exist some
![]() $t_{0}\in S^{1}$
and some constant
$t_{0}\in S^{1}$
and some constant
![]() $\unicode[STIX]{x1D716}>0$
, sequences
$\unicode[STIX]{x1D716}>0$
, sequences
![]() $\unicode[STIX]{x1D70F}_{k}\rightarrow \infty$
,
$\unicode[STIX]{x1D70F}_{k}\rightarrow \infty$
,
![]() $p_{k}>0$
such that
$p_{k}>0$
such that
Then combining this with the continuity of
![]() $w$
in
$w$
in
![]() $t$
, there exists some
$t$
, there exists some
![]() $l>0$
small such that
$l>0$
small such that
Therefore,
 $$\begin{eqnarray}\displaystyle & & \displaystyle \!\int _{S^{1}}d(w(\unicode[STIX]{x1D70F}_{k+p_{k}},t),w(\unicode[STIX]{x1D70F}_{k},t))\,dt\nonumber\\ \displaystyle & & \displaystyle \!\quad =\int _{|t-t_{0}|\leqslant l}d(w(\unicode[STIX]{x1D70F}_{k+p_{k}},t),w(\unicode[STIX]{x1D70F}_{k},t))\,dt+\!\int _{|t-t_{0}|>l}d(w(\unicode[STIX]{x1D70F}_{k+p_{k}},t),w(\unicode[STIX]{x1D70F}_{k},t))\,dt\nonumber\\ \displaystyle & & \displaystyle \!\quad \geqslant \int _{|t-t_{0}|\leqslant l}d(w(\unicode[STIX]{x1D70F}_{k+p_{k}},t),w(\unicode[STIX]{x1D70F}_{k},t))\,dt\geqslant \unicode[STIX]{x1D716}l.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \!\int _{S^{1}}d(w(\unicode[STIX]{x1D70F}_{k+p_{k}},t),w(\unicode[STIX]{x1D70F}_{k},t))\,dt\nonumber\\ \displaystyle & & \displaystyle \!\quad =\int _{|t-t_{0}|\leqslant l}d(w(\unicode[STIX]{x1D70F}_{k+p_{k}},t),w(\unicode[STIX]{x1D70F}_{k},t))\,dt+\!\int _{|t-t_{0}|>l}d(w(\unicode[STIX]{x1D70F}_{k+p_{k}},t),w(\unicode[STIX]{x1D70F}_{k},t))\,dt\nonumber\\ \displaystyle & & \displaystyle \!\quad \geqslant \int _{|t-t_{0}|\leqslant l}d(w(\unicode[STIX]{x1D70F}_{k+p_{k}},t),w(\unicode[STIX]{x1D70F}_{k},t))\,dt\geqslant \unicode[STIX]{x1D716}l.\nonumber\end{eqnarray}$$
On the other hand, we compute
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{S^{1}}d(w(\unicode[STIX]{x1D70F}_{k+p_{k}},t),w(\unicode[STIX]{x1D70F}_{k},t))\,dt\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \int _{S^{1}}\int _{\unicode[STIX]{x1D70F}_{k}}^{\unicode[STIX]{x1D70F}_{k+p_{k}}}\left|\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}s}(s,t)\right|ds\,dt=\int _{\unicode[STIX]{x1D70F}_{k}}^{\unicode[STIX]{x1D70F}_{k+p_{k}}}\int _{S^{1}}\left|\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}s}(s,t)\right|dt\,ds\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \int _{\unicode[STIX]{x1D70F}_{k}}^{\unicode[STIX]{x1D70F}_{k+p_{k}}}\left(\int _{S^{1}}\left|\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}s}(s,t)\right|^{2}dt\right)^{1/2}ds\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \int _{\unicode[STIX]{x1D70F}_{k}}^{\unicode[STIX]{x1D70F}_{k+p_{k}}}Ce^{-\unicode[STIX]{x1D6FF}s}\,ds=\frac{C}{\unicode[STIX]{x1D6FF}}(1-e^{-(\unicode[STIX]{x1D70F}_{k+p_{k}}-\unicode[STIX]{x1D70F}_{k})})e^{-\unicode[STIX]{x1D70F}_{k}}\leqslant \frac{C}{\unicode[STIX]{x1D6FF}}e^{-\unicode[STIX]{x1D70F}_{k}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{S^{1}}d(w(\unicode[STIX]{x1D70F}_{k+p_{k}},t),w(\unicode[STIX]{x1D70F}_{k},t))\,dt\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \int _{S^{1}}\int _{\unicode[STIX]{x1D70F}_{k}}^{\unicode[STIX]{x1D70F}_{k+p_{k}}}\left|\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}s}(s,t)\right|ds\,dt=\int _{\unicode[STIX]{x1D70F}_{k}}^{\unicode[STIX]{x1D70F}_{k+p_{k}}}\int _{S^{1}}\left|\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}s}(s,t)\right|dt\,ds\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \int _{\unicode[STIX]{x1D70F}_{k}}^{\unicode[STIX]{x1D70F}_{k+p_{k}}}\left(\int _{S^{1}}\left|\frac{\unicode[STIX]{x2202}w}{\unicode[STIX]{x2202}s}(s,t)\right|^{2}dt\right)^{1/2}ds\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \int _{\unicode[STIX]{x1D70F}_{k}}^{\unicode[STIX]{x1D70F}_{k+p_{k}}}Ce^{-\unicode[STIX]{x1D6FF}s}\,ds=\frac{C}{\unicode[STIX]{x1D6FF}}(1-e^{-(\unicode[STIX]{x1D70F}_{k+p_{k}}-\unicode[STIX]{x1D70F}_{k})})e^{-\unicode[STIX]{x1D70F}_{k}}\leqslant \frac{C}{\unicode[STIX]{x1D6FF}}e^{-\unicode[STIX]{x1D70F}_{k}}.\nonumber\end{eqnarray}$$
When
![]() $\unicode[STIX]{x1D70F}_{k}$
sufficiently large, this inequality gives rise to a contradiction to (11.34). Hence the proof.◻
$\unicode[STIX]{x1D70F}_{k}$
sufficiently large, this inequality gives rise to a contradiction to (11.34). Hence the proof.◻
Now using the subsequence convergence from Theorem 9.4, we can pick a subsequence
![]() $\{\unicode[STIX]{x1D70F}_{k}\}$
and a closed Reeb orbit
$\{\unicode[STIX]{x1D70F}_{k}\}$
and a closed Reeb orbit
![]() $(\unicode[STIX]{x1D6FE},T)$
such that
$(\unicode[STIX]{x1D6FE},T)$
such that
uniformly in
![]() $t$
. Then the above lemma immediately implies
$t$
. Then the above lemma immediately implies
![]() $w(\unicode[STIX]{x1D70F},t)$
uniformly converges to
$w(\unicode[STIX]{x1D70F},t)$
uniformly converges to
![]() $z(t)$
for any
$z(t)$
for any
![]() $t\in S^{1}$
.
$t\in S^{1}$
.
It remains to show that this convergence is uniform in
![]() $t$
. Suppose to the contrary that there exist some
$t$
. Suppose to the contrary that there exist some
![]() $\unicode[STIX]{x1D716}>0$
and some sequence
$\unicode[STIX]{x1D716}>0$
and some sequence
![]() $(\unicode[STIX]{x1D70F}_{k},t_{k})$
such that
$(\unicode[STIX]{x1D70F}_{k},t_{k})$
such that
Since
![]() $t_{k}\in S^{1}$
, we can further take a subsequence, still denoted by
$t_{k}\in S^{1}$
, we can further take a subsequence, still denoted by
![]() $t_{k}$
, such that
$t_{k}$
, such that
![]() $t_{k}\rightarrow t_{0}\in S^{1}$
. We can take
$t_{k}\rightarrow t_{0}\in S^{1}$
. We can take
![]() $k$
so large that
$k$
so large that
![]() $d(z(t_{k}),z(t_{0}))\leqslant (1/2)\unicode[STIX]{x1D716}$
. We also note
$d(z(t_{k}),z(t_{0}))\leqslant (1/2)\unicode[STIX]{x1D716}$
. We also note
by which we can make the distance less than
![]() $(1/2)\unicode[STIX]{x1D716}$
by taking
$(1/2)\unicode[STIX]{x1D716}$
by taking
![]() $k$
sufficiently large.
$k$
sufficiently large.
Combing these, we derive
 $$\begin{eqnarray}\displaystyle d(w(\unicode[STIX]{x1D70F}_{k},t_{0}),z(t_{0})) & {\geqslant} & \displaystyle d(w(\unicode[STIX]{x1D70F}_{k},t_{k}),z(t_{k}))-d(w(\unicode[STIX]{x1D70F}_{k},t_{k}),w(\unicode[STIX]{x1D70F}_{k},t_{0}))\nonumber\\ \displaystyle & & \displaystyle -\,d(z(t_{k}),z(t_{0}))\nonumber\\ \displaystyle & {\geqslant} & \displaystyle 2\unicode[STIX]{x1D716}-{\textstyle \frac{1}{2}}\unicode[STIX]{x1D716}-{\textstyle \frac{1}{2}}\unicode[STIX]{x1D716}=\unicode[STIX]{x1D716}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle d(w(\unicode[STIX]{x1D70F}_{k},t_{0}),z(t_{0})) & {\geqslant} & \displaystyle d(w(\unicode[STIX]{x1D70F}_{k},t_{k}),z(t_{k}))-d(w(\unicode[STIX]{x1D70F}_{k},t_{k}),w(\unicode[STIX]{x1D70F}_{k},t_{0}))\nonumber\\ \displaystyle & & \displaystyle -\,d(z(t_{k}),z(t_{0}))\nonumber\\ \displaystyle & {\geqslant} & \displaystyle 2\unicode[STIX]{x1D716}-{\textstyle \frac{1}{2}}\unicode[STIX]{x1D716}-{\textstyle \frac{1}{2}}\unicode[STIX]{x1D716}=\unicode[STIX]{x1D716}\nonumber\end{eqnarray}$$
for all sufficiently large
![]() $k$
’s. This gives rise to contradiction to the pointwise convergence
$k$
’s. This gives rise to contradiction to the pointwise convergence
![]() $w(\unicode[STIX]{x1D70F}_{k},t_{k})\rightarrow z(t_{0})$
, which finishes the proof of uniform convergence for
$w(\unicode[STIX]{x1D70F}_{k},t_{k})\rightarrow z(t_{0})$
, which finishes the proof of uniform convergence for
![]() $t\in S^{1}$
and hence completes the proof.◻
$t\in S^{1}$
and hence completes the proof.◻
Then the following
![]() $C^{0}$
-exponential convergence immediately follows.
$C^{0}$
-exponential convergence immediately follows.
Proposition 11.23. There exist some constants
![]() $C>0$
,
$C>0$
,
![]() $\unicode[STIX]{x1D6FF}>0$
and
$\unicode[STIX]{x1D6FF}>0$
and
![]() $\unicode[STIX]{x1D70F}_{0}$
large such that for any
$\unicode[STIX]{x1D70F}_{0}$
large such that for any
![]() $\unicode[STIX]{x1D70F}>\unicode[STIX]{x1D70F}_{0}$
,
$\unicode[STIX]{x1D70F}>\unicode[STIX]{x1D70F}_{0}$
,
Proof. For any
![]() $\unicode[STIX]{x1D70F}<\unicode[STIX]{x1D70F}_{+}$
, similarly as in the previous proof,
$\unicode[STIX]{x1D70F}<\unicode[STIX]{x1D70F}_{+}$
, similarly as in the previous proof,
Take
![]() $\unicode[STIX]{x1D70F}_{+}\rightarrow +\infty$
and using the
$\unicode[STIX]{x1D70F}_{+}\rightarrow +\infty$
and using the
![]() $C^{0}$
convergence of
$C^{0}$
convergence of
![]() $w$
part, that is, Proposition 11.21, we get
$w$
part, that is, Proposition 11.21, we get
This proves the first inequality. ◻
11.7
 $C^{\infty }$
-exponential decay of
$C^{\infty }$
-exponential decay of
 $dw-X_{\unicode[STIX]{x1D706}}(w)\,d\unicode[STIX]{x1D70F}$
$dw-X_{\unicode[STIX]{x1D706}}(w)\,d\unicode[STIX]{x1D70F}$
We recall the coordinate expression of
![]() $w=(u,e)$
under the identification of a tubular neighborhood of
$w=(u,e)$
under the identification of a tubular neighborhood of
![]() $Q$
with a neighborhood of the zero section of the normal bundle of
$Q$
with a neighborhood of the zero section of the normal bundle of
![]() $Q$
. So far, we have established the following:
$Q$
. So far, we have established the following:
∙
 $W^{1,2}$
-exponential decay of the normal component
$W^{1,2}$
-exponential decay of the normal component
 $e$
;
$e$
;∙
 $L^{2}$
-exponential decay of the derivative
$L^{2}$
-exponential decay of the derivative
 $du$
of the base component
$du$
of the base component
 $u$
;
$u$
;∙
 $C^{0}$
-exponential convergence of
$C^{0}$
-exponential convergence of
 $w(\unicode[STIX]{x1D70F},\cdot )\rightarrow z(\cdot )$
as
$w(\unicode[STIX]{x1D70F},\cdot )\rightarrow z(\cdot )$
as
 $\unicode[STIX]{x1D70F}\rightarrow \infty$
for some closed Reeb orbit
$\unicode[STIX]{x1D70F}\rightarrow \infty$
for some closed Reeb orbit
 $z$
.
$z$
.
Now we are ready to complete the proof of
![]() $C^{\infty }$
-exponential convergence
$C^{\infty }$
-exponential convergence
![]() $w(\unicode[STIX]{x1D70F},\cdot )\rightarrow z$
by establishing the
$w(\unicode[STIX]{x1D70F},\cdot )\rightarrow z$
by establishing the
![]() $C^{\infty }$
-exponential decay of
$C^{\infty }$
-exponential decay of
![]() $dw-X_{\unicode[STIX]{x1D706}}(w)\,dt$
. The proof of the latter decay is now in order which will be carried out by the bootstrapping arguments applied to the system (11.4).
$dw-X_{\unicode[STIX]{x1D706}}(w)\,dt$
. The proof of the latter decay is now in order which will be carried out by the bootstrapping arguments applied to the system (11.4).
Combining the above three, we have obtained
![]() $L^{2}$
-exponential estimates of the full derivative
$L^{2}$
-exponential estimates of the full derivative
![]() $dw$
. As already used in Section 11.5, we consider the equation
$dw$
. As already used in Section 11.5, we consider the equation
where
![]() $\unicode[STIX]{x1D706}=f\unicode[STIX]{x1D706}_{E}$
, under Hypothesis 9.7. By the bootstrapping argument using the local uniform a priori estimates on the cylindrical region (see [Reference Oh and WangOW2] for the details), we obtain higher-order
$\unicode[STIX]{x1D706}=f\unicode[STIX]{x1D706}_{E}$
, under Hypothesis 9.7. By the bootstrapping argument using the local uniform a priori estimates on the cylindrical region (see [Reference Oh and WangOW2] for the details), we obtain higher-order
![]() $W^{k,2}$
-exponential decays of the term
$W^{k,2}$
-exponential decays of the term
for all
![]() $k\geqslant 0$
, where
$k\geqslant 0$
, where
![]() $w(\unicode[STIX]{x1D70F},\cdot )$
converges to
$w(\unicode[STIX]{x1D70F},\cdot )$
converges to
![]() $z$
as
$z$
as
![]() $\unicode[STIX]{x1D70F}\rightarrow \infty$
in
$\unicode[STIX]{x1D70F}\rightarrow \infty$
in
![]() $C^{0}$
sense. This, combined with the Sobolev’s embedding, then completes proof of
$C^{0}$
sense. This, combined with the Sobolev’s embedding, then completes proof of
![]() $C^{\infty }$
-convergence of
$C^{\infty }$
-convergence of
![]() $w(\unicode[STIX]{x1D70F},\cdot )\rightarrow z$
as
$w(\unicode[STIX]{x1D70F},\cdot )\rightarrow z$
as
![]() $\unicode[STIX]{x1D70F}\rightarrow \infty$
.
$\unicode[STIX]{x1D70F}\rightarrow \infty$
.
12 Exponential decay: general Morse–Bott case
In this section, we consider the general case of the Morse–Bott submanifold. For this one, it is enough to consider the normalized contact triad
![]() $(F,f\unicode[STIX]{x1D706}_{F},J)$
where
$(F,f\unicode[STIX]{x1D706}_{F},J)$
where
![]() $J$
is adapted to the zero section
$J$
is adapted to the zero section
![]() $Q$
.
$Q$
.
Write
![]() $w=(u,s)=(u,\unicode[STIX]{x1D707},e)$
, where
$w=(u,s)=(u,\unicode[STIX]{x1D707},e)$
, where
![]() $\unicode[STIX]{x1D707}\in u^{\ast }JT{\mathcal{N}}$
and
$\unicode[STIX]{x1D707}\in u^{\ast }JT{\mathcal{N}}$
and
![]() $e\in u^{\ast }E$
. By the calculations in Section 7, and with similar calculation of Section 11, the
$e\in u^{\ast }E$
. By the calculations in Section 7, and with similar calculation of Section 11, the
![]() $e$
part can be dealt with exactly the same as in the prequantization case, whose details are skipped here.
$e$
part can be dealt with exactly the same as in the prequantization case, whose details are skipped here.
After the
![]() $e$
-part is taken care of, for the
$e$
-part is taken care of, for the
![]() $(u,\unicode[STIX]{x1D707})$
part, we derive
$(u,\unicode[STIX]{x1D707})$
part, we derive
 $$\begin{eqnarray}\left(\begin{array}{@{}c@{}}\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}{\displaystyle \frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}}\\ \unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D707}\end{array}\right)+J\left(\begin{array}{@{}c@{}}\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}{\displaystyle \frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}t}}\\ \unicode[STIX]{x1D6FB}_{t}\unicode[STIX]{x1D707}\end{array}\right)=L,\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}c@{}}\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}{\displaystyle \frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}\unicode[STIX]{x1D70F}}}\\ \unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D707}\end{array}\right)+J\left(\begin{array}{@{}c@{}}\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D703}}{\displaystyle \frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}t}}\\ \unicode[STIX]{x1D6FB}_{t}\unicode[STIX]{x1D707}\end{array}\right)=L,\end{eqnarray}$$
where
![]() $|L|\leqslant Ce^{-\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70F}}$
similarly as for the prequantization case.
$|L|\leqslant Ce^{-\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70F}}$
similarly as for the prequantization case.
Then we apply the three-interval argument whose details are similar to the prequantization case and so are omitted. We only need to establish as in the prequantization case for the limiting
![]() $(\overline{\unicode[STIX]{x1D701}}_{\infty },\overline{\unicode[STIX]{x1D707}}_{\infty })$
is not in kernel of
$(\overline{\unicode[STIX]{x1D701}}_{\infty },\overline{\unicode[STIX]{x1D707}}_{\infty })$
is not in kernel of
![]() $B_{\infty }$
.
$B_{\infty }$
.
If
![]() $(\overline{\unicode[STIX]{x1D701}}_{\infty },\overline{\unicode[STIX]{x1D707}}_{\infty })$
is in the kernel of
$(\overline{\unicode[STIX]{x1D701}}_{\infty },\overline{\unicode[STIX]{x1D707}}_{\infty })$
is in the kernel of
![]() $B_{\infty }$
, then by the Morse–Bott condition, we have
$B_{\infty }$
, then by the Morse–Bott condition, we have
![]() $\overline{\unicode[STIX]{x1D707}}_{\infty }=0$
. With the same procedure for introducing the center of mass, we can use the same argument to prove that
$\overline{\unicode[STIX]{x1D707}}_{\infty }=0$
. With the same procedure for introducing the center of mass, we can use the same argument to prove that
![]() $\overline{\unicode[STIX]{x1D701}}_{\infty }$
must vanish if it is contained in the kernel of
$\overline{\unicode[STIX]{x1D701}}_{\infty }$
must vanish if it is contained in the kernel of
![]() $B_{\infty }$
. This will then prove the following proposition.
$B_{\infty }$
. This will then prove the following proposition.
Proposition 12.1. For any
![]() $k=0,1,\ldots ,$
there exists some constant
$k=0,1,\ldots ,$
there exists some constant
![]() $C_{k}>0$
and
$C_{k}>0$
and
![]() $\unicode[STIX]{x1D6FF}_{k}>0$
$\unicode[STIX]{x1D6FF}_{k}>0$
for each
![]() $k\geqslant 0$
.
$k\geqslant 0$
.
13 The case of asymptotically cylindrical symplectic manifolds
In this section, we explain how we can apply the three-interval method and our tensorial scheme to noncompact symplectic manifolds with asymptotically cylindrical ends. Here we use Bao’s precise definition [Reference BaoBa] of the asymptotically cylindrical ends but restricted to the case where the asymptotical manifold is a contact manifold
![]() $(V,\unicode[STIX]{x1D709})$
. In this section, we denote a contact manifold by
$(V,\unicode[STIX]{x1D709})$
. In this section, we denote a contact manifold by
![]() $V$
, instead of
$V$
, instead of
![]() $M$
which is what we used in the previous sections, to make comparison of our definition with Bao’s transparent.
$M$
which is what we used in the previous sections, to make comparison of our definition with Bao’s transparent.
Let
![]() $(V,\unicode[STIX]{x1D709})$
be a closed contact manifold of dimension
$(V,\unicode[STIX]{x1D709})$
be a closed contact manifold of dimension
![]() $2n+1$
and let
$2n+1$
and let
![]() $J$
be an almost complex structure on
$J$
be an almost complex structure on
![]() $W=[0,\infty )\times V$
. We denote
$W=[0,\infty )\times V$
. We denote
a smooth vector field on
![]() $W$
, and let
$W$
, and let
![]() $\unicode[STIX]{x1D709}\subset TW$
be a subbundle defined by
$\unicode[STIX]{x1D709}\subset TW$
be a subbundle defined by
Then we have splitting
and denote by
![]() $i:\mathbb{R}\{\unicode[STIX]{x2202}/\unicode[STIX]{x2202}r\}\oplus \mathbb{R}\{\mathbf{R}\}\rightarrow \mathbb{R}\{\unicode[STIX]{x2202}/\unicode[STIX]{x2202}r\}\oplus \mathbb{R}\{\mathbf{R}\}$
the almost complex structure
$i:\mathbb{R}\{\unicode[STIX]{x2202}/\unicode[STIX]{x2202}r\}\oplus \mathbb{R}\{\mathbf{R}\}\rightarrow \mathbb{R}\{\unicode[STIX]{x2202}/\unicode[STIX]{x2202}r\}\oplus \mathbb{R}\{\mathbf{R}\}$
the almost complex structure
We denote by
![]() $\unicode[STIX]{x1D706}$
and
$\unicode[STIX]{x1D706}$
and
![]() $\unicode[STIX]{x1D70E}$
the dual 1-forms of
$\unicode[STIX]{x1D70E}$
the dual 1-forms of
![]() $\unicode[STIX]{x2202}/\unicode[STIX]{x2202}r$
and
$\unicode[STIX]{x2202}/\unicode[STIX]{x2202}r$
and
![]() $\mathbf{R}$
such that
$\mathbf{R}$
such that
![]() $\unicode[STIX]{x1D706}|_{\unicode[STIX]{x1D709}}=0=\unicode[STIX]{x1D70E}|_{\unicode[STIX]{x1D709}}$
. In particular,
$\unicode[STIX]{x1D706}|_{\unicode[STIX]{x1D709}}=0=\unicode[STIX]{x1D70E}|_{\unicode[STIX]{x1D709}}$
. In particular,
We denote by
![]() $T_{s}:[0,\infty )\times V\rightarrow [-s,\infty )\times V$
the translation
$T_{s}:[0,\infty )\times V\rightarrow [-s,\infty )\times V$
the translation
![]() $T_{s}(r,v)=(r+s,v)$
and call a tensor on
$T_{s}(r,v)=(r+s,v)$
and call a tensor on
![]() $W$
is translational invariant if it is invariant under the translation.
$W$
is translational invariant if it is invariant under the translation.
The following definition is the special case of the one in [Reference BaoBa] restricted to the contact-type asymptotical boundary.
Definition 13.1. (Asymptotically cylindrical
![]() $(W,\unicode[STIX]{x1D714},J)$
[Reference BaoBa]) The almost complex structure is called
$(W,\unicode[STIX]{x1D714},J)$
[Reference BaoBa]) The almost complex structure is called
![]() $C^{\ell }$
-asymptotically cylindrical if there exists a 2-form
$C^{\ell }$
-asymptotically cylindrical if there exists a 2-form
![]() $\unicode[STIX]{x1D714}$
on
$\unicode[STIX]{x1D714}$
on
![]() $W$
such that the pair
$W$
such that the pair
![]() $(J,\unicode[STIX]{x1D714})$
satisfies the following:
$(J,\unicode[STIX]{x1D714})$
satisfies the following:
-
 $\text{(AC1)}$
$\text{(AC1)}$
 $\unicode[STIX]{x2202}/\unicode[STIX]{x2202}r\!\rfloor \unicode[STIX]{x1D714}=0=\mathbf{R}\!\rfloor \unicode[STIX]{x1D714}$
;
$\unicode[STIX]{x2202}/\unicode[STIX]{x2202}r\!\rfloor \unicode[STIX]{x1D714}=0=\mathbf{R}\!\rfloor \unicode[STIX]{x1D714}$
;-
 $\text{(AC2)}$
$\text{(AC2)}$
 $\unicode[STIX]{x1D714}|_{\unicode[STIX]{x1D709}}(v,J\,v)\geqslant 0$
and equality holds if and only if
$\unicode[STIX]{x1D714}|_{\unicode[STIX]{x1D709}}(v,J\,v)\geqslant 0$
and equality holds if and only if
 $v=0$
;
$v=0$
;-
 $\text{(AC3)}$
$\text{(AC3)}$
there exists a smooth translational invariant almost complex structure
 $J_{\infty }$
on
$J_{\infty }$
on
 $\mathbb{R}\times V$
and constants
$\mathbb{R}\times V$
and constants
 $R_{\ell }>0$
and
$R_{\ell }>0$
and
 $C_{\ell }$
,
$C_{\ell }$
,
 $\unicode[STIX]{x1D6FF}_{\ell }>0$
$\unicode[STIX]{x1D6FF}_{\ell }>0$
 $$\begin{eqnarray}\Vert (J-J_{\infty })|_{[r,\infty )\times V}\Vert _{C^{\ell }}\leqslant C_{\ell }e^{-\unicode[STIX]{x1D6FF}_{\ell }r}\end{eqnarray}$$
$$\begin{eqnarray}\Vert (J-J_{\infty })|_{[r,\infty )\times V}\Vert _{C^{\ell }}\leqslant C_{\ell }e^{-\unicode[STIX]{x1D6FF}_{\ell }r}\end{eqnarray}$$
for all
 $r\geqslant R_{\ell }$
. Here the norm is computed in terms of the translational invariant metric
$r\geqslant R_{\ell }$
. Here the norm is computed in terms of the translational invariant metric
 $g_{\infty }$
and a translational invariant connection;
$g_{\infty }$
and a translational invariant connection;-
 $\text{(AC4)}$
$\text{(AC4)}$
there exists a smooth translational invariant closed 2-form
 $\unicode[STIX]{x1D714}_{\infty }$
on
$\unicode[STIX]{x1D714}_{\infty }$
on
 $\mathbb{R}\times V$
such that
$\mathbb{R}\times V$
such that  $$\begin{eqnarray}\Vert (\unicode[STIX]{x1D714}-\unicode[STIX]{x1D714}_{\infty })|_{[r,\infty )\times V}\Vert _{C^{\ell }}\leqslant C_{\ell }e^{-\unicode[STIX]{x1D6FF}_{\ell }r}\end{eqnarray}$$
$$\begin{eqnarray}\Vert (\unicode[STIX]{x1D714}-\unicode[STIX]{x1D714}_{\infty })|_{[r,\infty )\times V}\Vert _{C^{\ell }}\leqslant C_{\ell }e^{-\unicode[STIX]{x1D6FF}_{\ell }r}\end{eqnarray}$$
for all
 $r\geqslant R_{\ell }$
;
$r\geqslant R_{\ell }$
;-
 $\text{(AC5)}$
$\text{(AC5)}$
 $(J_{\infty },\unicode[STIX]{x1D714}_{\infty })$
satisfies (AC1) and (AC2);
$(J_{\infty },\unicode[STIX]{x1D714}_{\infty })$
satisfies (AC1) and (AC2);-
 $\text{(AC6)}$
$\text{(AC6)}$
 $\mathbf{R}_{\infty }\!\rfloor d\unicode[STIX]{x1D706}_{\infty }=0$
, where
$\mathbf{R}_{\infty }\!\rfloor d\unicode[STIX]{x1D706}_{\infty }=0$
, where
 $\mathbf{R}_{\infty }:=\lim _{s\rightarrow \infty }T_{s}^{\ast }\mathbf{R}$
,
$\mathbf{R}_{\infty }:=\lim _{s\rightarrow \infty }T_{s}^{\ast }\mathbf{R}$
,
 $\unicode[STIX]{x1D706}_{\infty }:=\lim _{s\rightarrow \infty }T_{s}^{\ast }\unicode[STIX]{x1D706}$
where both limit exist on
$\unicode[STIX]{x1D706}_{\infty }:=\lim _{s\rightarrow \infty }T_{s}^{\ast }\unicode[STIX]{x1D706}$
where both limit exist on
 $\mathbb{R}\times V$
by (AC3);
$\mathbb{R}\times V$
by (AC3);-
 $\text{(AC7)}$
$\text{(AC7)}$
 $\mathbf{R}_{\infty }(r,v)=J_{\infty }(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}r)\in T_{(r,v)}(\{r\}\times V)$
.
$\mathbf{R}_{\infty }(r,v)=J_{\infty }(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}r)\in T_{(r,v)}(\{r\}\times V)$
.
For the purpose of current paper, we restrict ourselves to the case when
![]() $\unicode[STIX]{x1D706}_{\infty }$
is a contact form of a contact manifold
$\unicode[STIX]{x1D706}_{\infty }$
is a contact form of a contact manifold
![]() $(V,\unicode[STIX]{x1D709})$
and
$(V,\unicode[STIX]{x1D709})$
and
![]() $\mathbf{R}$
the translational invariant vector field induced by the Reeb vector field on
$\mathbf{R}$
the translational invariant vector field induced by the Reeb vector field on
![]() $V$
associated to the contact form
$V$
associated to the contact form
![]() $\unicode[STIX]{x1D706}_{\infty }$
of
$\unicode[STIX]{x1D706}_{\infty }$
of
![]() $(V,\unicode[STIX]{x1D709})$
. More precisely, we have
$(V,\unicode[STIX]{x1D709})$
. More precisely, we have
with respect to the canonical splitting
![]() $T_{(r,v)}W=\mathbb{R}\oplus T_{v}V$
. Furthermore, we also assume that
$T_{(r,v)}W=\mathbb{R}\oplus T_{v}V$
. Furthermore, we also assume that
![]() $(V,\unicode[STIX]{x1D706}_{\infty },J_{\infty })$
is a contact triad.
$(V,\unicode[STIX]{x1D706}_{\infty },J_{\infty })$
is a contact triad.
Now suppose that
![]() $Q\subset V$
is a Morse–Bott submanifold of closed Reeb orbits of
$Q\subset V$
is a Morse–Bott submanifold of closed Reeb orbits of
![]() $\unicode[STIX]{x1D706}_{\infty }$
and that
$\unicode[STIX]{x1D706}_{\infty }$
and that
![]() $\widetilde{u}:[0,\infty )\times S^{1}\rightarrow W$
is a
$\widetilde{u}:[0,\infty )\times S^{1}\rightarrow W$
is a
![]() $\widetilde{J}$
-holomorphic curve for which the Subsequence theorem given in [Reference BaoBa, Section 3.2] holds. We also assume that
$\widetilde{J}$
-holomorphic curve for which the Subsequence theorem given in [Reference BaoBa, Section 3.2] holds. We also assume that
![]() $J_{\infty }$
is adapted to
$J_{\infty }$
is adapted to
![]() $Q$
in the sense of Definition 8.2. Let
$Q$
in the sense of Definition 8.2. Let
![]() $\unicode[STIX]{x1D70F}_{k}\rightarrow \infty$
be a sequence such that
$\unicode[STIX]{x1D70F}_{k}\rightarrow \infty$
be a sequence such that
![]() $a(\unicode[STIX]{x1D70F}_{k},t)\rightarrow \infty$
and
$a(\unicode[STIX]{x1D70F}_{k},t)\rightarrow \infty$
and
![]() $w(\unicode[STIX]{x1D70F}_{k},t)\rightarrow z$
uniformly as
$w(\unicode[STIX]{x1D70F}_{k},t)\rightarrow z$
uniformly as
![]() $k\rightarrow \infty$
where
$k\rightarrow \infty$
where
![]() $z$
is a closed Reeb orbit whose image is contained in
$z$
is a closed Reeb orbit whose image is contained in
![]() $Q$
. By the local uniform elliptic estimates, we may assume that the same uniform convergence holds on the intervals
$Q$
. By the local uniform elliptic estimates, we may assume that the same uniform convergence holds on the intervals
as
![]() $k\rightarrow \infty$
. On these intervals, we can write the equation
$k\rightarrow \infty$
. On these intervals, we can write the equation
![]() $\overline{\unicode[STIX]{x2202}}_{\widetilde{J}}\,\widetilde{u}=0$
as
$\overline{\unicode[STIX]{x2202}}_{\widetilde{J}}\,\widetilde{u}=0$
as
We can write the endomorphism
![]() $(\widetilde{J}-J_{\infty })(r,\unicode[STIX]{x1D6E9})=:M(r,\unicode[STIX]{x1D6E9})$
where
$(\widetilde{J}-J_{\infty })(r,\unicode[STIX]{x1D6E9})=:M(r,\unicode[STIX]{x1D6E9})$
where
![]() $(r,\unicode[STIX]{x1D6E9})\in \mathbb{R}\times V$
so that
$(r,\unicode[STIX]{x1D6E9})\in \mathbb{R}\times V$
so that
for all
![]() $r\geqslant R_{0}$
. Therefore,
$r\geqslant R_{0}$
. Therefore,
![]() $u=(a,w)$
with
$u=(a,w)$
with
![]() $a=r\circ \widetilde{u}$
,
$a=r\circ \widetilde{u}$
,
![]() $w=\unicode[STIX]{x1D6E9}\circ \widetilde{u}$
satisfies
$w=\unicode[STIX]{x1D6E9}\circ \widetilde{u}$
satisfies
Decomposing
![]() $\overline{\unicode[STIX]{x2202}}_{J_{\infty }}\widetilde{u}$
and
$\overline{\unicode[STIX]{x2202}}_{J_{\infty }}\widetilde{u}$
and
![]() $\unicode[STIX]{x2202}\widetilde{u}/\unicode[STIX]{x2202}t$
with respect to the decomposition
$\unicode[STIX]{x2202}\widetilde{u}/\unicode[STIX]{x2202}t$
with respect to the decomposition
we have derived
where
![]() $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D709}}$
is the projection to
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D709}}$
is the projection to
![]() $\unicode[STIX]{x1D709}$
with respect to the contact form
$\unicode[STIX]{x1D709}$
with respect to the contact form
![]() $\unicode[STIX]{x1D706}_{\infty }$
and
$\unicode[STIX]{x1D706}_{\infty }$
and
![]() $\unicode[STIX]{x1D70B}_{\mathbb{C}}$
is the projection to
$\unicode[STIX]{x1D70B}_{\mathbb{C}}$
is the projection to
![]() $\mathbb{R}\cdot \unicode[STIX]{x2202}/\unicode[STIX]{x2202}r\oplus \mathbb{R}\cdot X_{\unicode[STIX]{x1D706}_{\infty }}$
with respect to the cylindrical
$\mathbb{R}\cdot \unicode[STIX]{x2202}/\unicode[STIX]{x2202}r\oplus \mathbb{R}\cdot X_{\unicode[STIX]{x1D706}_{\infty }}$
with respect to the cylindrical
![]() $(W,\unicode[STIX]{x1D714}_{\infty },J_{\infty })$
. Then we obtain from (13.4)
$(W,\unicode[STIX]{x1D714}_{\infty },J_{\infty })$
. Then we obtain from (13.4)
as
![]() $a\rightarrow \infty$
. By the subsequence convergence theorem assumption and local a priori estimates on
$a\rightarrow \infty$
. By the subsequence convergence theorem assumption and local a priori estimates on
![]() $\widetilde{u}$
, we have immediately obtained the following
$\widetilde{u}$
, we have immediately obtained the following
where
![]() $w=\exp _{Z}(\unicode[STIX]{x1D709}_{G}+\unicode[STIX]{x1D709}_{{\mathcal{F}}}+e)$
is the decomposition similarly as before. Now we can apply exactly the same proof as the one given in the previous section to establish the exponential decay property of
$w=\exp _{Z}(\unicode[STIX]{x1D709}_{G}+\unicode[STIX]{x1D709}_{{\mathcal{F}}}+e)$
is the decomposition similarly as before. Now we can apply exactly the same proof as the one given in the previous section to establish the exponential decay property of
![]() $dw$
.
$dw$
.
For the component
![]() $a$
, we can use (13.6) and the argument used in [Reference Oh and WangOW2] and obtain the necessary exponential property as before.
$a$
, we can use (13.6) and the argument used in [Reference Oh and WangOW2] and obtain the necessary exponential property as before.
Acknowledgments
Rui Wang would like to thank Erkao Bao and Ke Zhu for useful discussions. Both authors are extremely grateful to the anonymous referee, who read the paper carefully, pointed out many typos and errors and provided valuable suggestions to improve the presentation of this paper.
Appendix A. Proof of Proposition 8.3
In this appendix, we prove contractibility of the set of
![]() $Q$
-adapted
$Q$
-adapted
![]() $CR$
-almost complex structures postponed from the proof of Proposition 8.3.
$CR$
-almost complex structures postponed from the proof of Proposition 8.3.
We first notice that for any
![]() $d\unicode[STIX]{x1D706}$
-compatible
$d\unicode[STIX]{x1D706}$
-compatible
![]() $CR$
-almost complex structure
$CR$
-almost complex structure
![]() $J$
,
$J$
,
![]() $(TQ\cap JTQ)\cap T{\mathcal{F}}=\{0\}$
: this is because for any
$(TQ\cap JTQ)\cap T{\mathcal{F}}=\{0\}$
: this is because for any
![]() $v\in (TQ\cap JTQ)\cap T{\mathcal{F}}$
,
$v\in (TQ\cap JTQ)\cap T{\mathcal{F}}$
,
since
![]() $Jv\in TQ$
and
$Jv\in TQ$
and
![]() $v\in T{\mathcal{F}}=\ker \unicode[STIX]{x1D714}_{Q}$
. Therefore,
$v\in T{\mathcal{F}}=\ker \unicode[STIX]{x1D714}_{Q}$
. Therefore,
![]() $(TQ\cap JTQ)$
and
$(TQ\cap JTQ)$
and
![]() $T{\mathcal{F}}$
are linearly independent.
$T{\mathcal{F}}$
are linearly independent.
We now give the following lemma.
Lemma A.1.
![]() $J$
satisfies the condition
$J$
satisfies the condition
![]() $JTQ\subset TQ+JT{\mathcal{N}}$
if and only if it satisfies
$JTQ\subset TQ+JT{\mathcal{N}}$
if and only if it satisfies
![]() $TQ=(TQ\cap JTQ)\oplus T{\mathcal{F}}$
.
$TQ=(TQ\cap JTQ)\oplus T{\mathcal{F}}$
.
Proof. It is obvious to see that
![]() $TQ=(TQ\cap JTQ)\oplus T{\mathcal{F}}$
indicates
$TQ=(TQ\cap JTQ)\oplus T{\mathcal{F}}$
indicates
![]() $J$
is
$J$
is
![]() $Q$
-adapted.
$Q$
-adapted.
It remains to prove the other direction. For this, we only need to prove that
![]() $TQ\subset (TQ\cap JTQ)+T{\mathcal{F}}$
by the discussion right in front of the statement of the lemma.
$TQ\subset (TQ\cap JTQ)+T{\mathcal{F}}$
by the discussion right in front of the statement of the lemma.
Let
![]() $v\in TQ$
. By the definition of the adapted condition,
$v\in TQ$
. By the definition of the adapted condition,
![]() $Jv\in TQ+JT{\mathcal{N}}$
. Therefore, we can write
$Jv\in TQ+JT{\mathcal{N}}$
. Therefore, we can write
for some
![]() $w\in TQ$
and
$w\in TQ$
and
![]() $u\in T{\mathcal{N}}$
. Then it follows that
$u\in T{\mathcal{N}}$
. Then it follows that
![]() $v=-Jw+u$
, noting that
$v=-Jw+u$
, noting that
![]() $Jw\in TQ\cap JTQ$
, we derive
$Jw\in TQ\cap JTQ$
, we derive
![]() $v\in (TQ\cap JTQ)+T{\mathcal{F}}$
and so we have finished the proof.◻
$v\in (TQ\cap JTQ)+T{\mathcal{F}}$
and so we have finished the proof.◻
This lemma shows that any
![]() $Q$
-adapted
$Q$
-adapted
![]() $J$
naturally defines a splitting
$J$
naturally defines a splitting
We also note that such
![]() $J$
preserves the subbundle
$J$
preserves the subbundle
![]() $TQ+JT{\mathcal{F}}\subset TM$
and so defines an invariant splitting
$TQ+JT{\mathcal{F}}\subset TM$
and so defines an invariant splitting
Conversely, for given splittings (A.1), (A.2), we can always choose
![]() $Q$
-adapted
$Q$
-adapted
![]() $J$
so that
$J$
so that
![]() $TQ\cap JTQ=G$
but the choice of such
$TQ\cap JTQ=G$
but the choice of such
![]() $J$
is not unique.
$J$
is not unique.
It is easy to see that the set of such splittings forms a contractible manifold (see [Reference Oh and ParkOP, Lemma 4.1] for a proof). We also note that the 2-form
![]() $d\unicode[STIX]{x1D706}$
induces nondegenerate (fiberwise) bilinear 2-forms on
$d\unicode[STIX]{x1D706}$
induces nondegenerate (fiberwise) bilinear 2-forms on
![]() $G$
and
$G$
and
![]() $E$
which we denote by
$E$
which we denote by
![]() $\unicode[STIX]{x1D714}_{G}$
and
$\unicode[STIX]{x1D714}_{G}$
and
![]() $\unicode[STIX]{x1D714}_{E}$
. Now we denote by
$\unicode[STIX]{x1D714}_{E}$
. Now we denote by
![]() ${\mathcal{J}}_{G,E}(\unicode[STIX]{x1D706};Q)$
the subset of
${\mathcal{J}}_{G,E}(\unicode[STIX]{x1D706};Q)$
the subset of
![]() ${\mathcal{J}}(\unicode[STIX]{x1D706};Q)$
consisting of
${\mathcal{J}}(\unicode[STIX]{x1D706};Q)$
consisting of
![]() $J\in {\mathcal{J}}(\unicode[STIX]{x1D706};Q)$
that satisfy (A.1), (A.2). Then
$J\in {\mathcal{J}}(\unicode[STIX]{x1D706};Q)$
that satisfy (A.1), (A.2). Then
![]() ${\mathcal{J}}(\unicode[STIX]{x1D706};Q)$
forms a fibration
${\mathcal{J}}(\unicode[STIX]{x1D706};Q)$
forms a fibration
Therefore, it is enough to prove that
![]() ${\mathcal{J}}_{G,E}(\unicode[STIX]{x1D706};Q)$
is contractible for each fixed
${\mathcal{J}}_{G,E}(\unicode[STIX]{x1D706};Q)$
is contractible for each fixed
![]() $G$
,
$G$
,
![]() $E$
.
$E$
.
We denote each
![]() $J:TM\rightarrow TM$
as a block
$J:TM\rightarrow TM$
as a block
![]() $4\times 4$
matrix in terms of the splitting
$4\times 4$
matrix in terms of the splitting
Then one can easily check that the
![]() $Q$
-adaptedness of
$Q$
-adaptedness of
![]() $J$
implies
$J$
implies
![]() $J$
must have the form
$J$
must have the form
 $$\begin{eqnarray}\left(\begin{array}{@{}cccc@{}}0 & 0 & \operatorname{Id} & 0\\ 0 & J_{G} & 0 & 0\\ -\operatorname{Id} & 0 & 0 & 0\\ 0 & B & 0 & J_{E}\end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}cccc@{}}0 & 0 & \operatorname{Id} & 0\\ 0 & J_{G} & 0 & 0\\ -\operatorname{Id} & 0 & 0 & 0\\ 0 & B & 0 & J_{E}\end{array}\right)\end{eqnarray}$$
where
![]() $J_{G}:G\rightarrow G$
is
$J_{G}:G\rightarrow G$
is
![]() $\unicode[STIX]{x1D714}_{G}$
-compatible and
$\unicode[STIX]{x1D714}_{G}$
-compatible and
![]() $J_{E}:E\rightarrow E$
is
$J_{E}:E\rightarrow E$
is
![]() $\unicode[STIX]{x1D714}_{E}$
-compatible, and
$\unicode[STIX]{x1D714}_{E}$
-compatible, and
![]() $B$
satisfies the relation
$B$
satisfies the relation
![]() $BJ_{G}=0$
which in turn implies
$BJ_{G}=0$
which in turn implies
![]() $B=0$
. Since each set of such
$B=0$
. Since each set of such
![]() $J_{G}$
’s or of such
$J_{G}$
’s or of such
![]() $J_{E}$
’s is contractible, it follows that
$J_{E}$
’s is contractible, it follows that
![]() ${\mathcal{J}}_{G,E}(\unicode[STIX]{x1D706};Q)$
is contractible. This finishes the proof of contractibility of
${\mathcal{J}}_{G,E}(\unicode[STIX]{x1D706};Q)$
is contractible. This finishes the proof of contractibility of
![]() ${\mathcal{J}}(\unicode[STIX]{x1D706};Q)$
.
${\mathcal{J}}(\unicode[STIX]{x1D706};Q)$
.
Appendix B. Proof of Theorem 9.4
In this appendix, we provide the proof of Theorem 9.4 borrowing the exposition from [Reference Oh and WangOW2].
For a given contact instanton
![]() $w:[0,\infty )\times S^{1}\rightarrow M$
, we define maps
$w:[0,\infty )\times S^{1}\rightarrow M$
, we define maps
![]() $w_{s}:[-s,\infty )\times S^{1}\rightarrow M$
by
$w_{s}:[-s,\infty )\times S^{1}\rightarrow M$
by
![]() $w_{s}(\unicode[STIX]{x1D70F},t)=w(\unicode[STIX]{x1D70F}+s,t)$
. For any compact set
$w_{s}(\unicode[STIX]{x1D70F},t)=w(\unicode[STIX]{x1D70F}+s,t)$
. For any compact set
![]() $K\subset \mathbb{R}$
, there exists sufficiently large
$K\subset \mathbb{R}$
, there exists sufficiently large
![]() $s_{0}$
such that for every
$s_{0}$
such that for every
![]() $s\geqslant s_{0}$
,
$s\geqslant s_{0}$
,
![]() $K\subset [-s,\infty )$
. For such
$K\subset [-s,\infty )$
. For such
![]() $s\geqslant s_{0}$
, we also get an
$s\geqslant s_{0}$
, we also get an
![]() $[s_{0},\infty )$
-family of maps by defining
$[s_{0},\infty )$
-family of maps by defining
![]() $w_{s}^{K}:=w_{s}|_{K\times S^{1}}:K\times S^{1}\rightarrow M$
.
$w_{s}^{K}:=w_{s}|_{K\times S^{1}}:K\times S^{1}\rightarrow M$
.
The asymptotic behavior of
![]() $w$
at infinity can be understood by studying the limit of the sequence of maps
$w$
at infinity can be understood by studying the limit of the sequence of maps
![]() $\{w_{s}^{K}:K\times S^{1}\rightarrow M\}_{s\in [s_{0},\infty )}$
, for any compact set
$\{w_{s}^{K}:K\times S^{1}\rightarrow M\}_{s\in [s_{0},\infty )}$
, for any compact set
![]() $K\subset \mathbb{R}$
.
$K\subset \mathbb{R}$
.
First of all, it is easy to check that under Hypothesis 9.1, the family
![]() $\{w_{s}^{K}:K\times S^{1}\rightarrow M\}_{s\in [s_{0},\infty )}$
satisfies the following:
$\{w_{s}^{K}:K\times S^{1}\rightarrow M\}_{s\in [s_{0},\infty )}$
satisfies the following:
(1)
 $\overline{\unicode[STIX]{x2202}}^{\unicode[STIX]{x1D70B}}w_{s}^{K}=0$
,
$\overline{\unicode[STIX]{x2202}}^{\unicode[STIX]{x1D70B}}w_{s}^{K}=0$
,
 $d((w_{s}^{K})^{\ast }\unicode[STIX]{x1D706}\circ j)=0$
, for every
$d((w_{s}^{K})^{\ast }\unicode[STIX]{x1D706}\circ j)=0$
, for every
 $s\in [s_{0},\infty )$
;
$s\in [s_{0},\infty )$
;(2)
 $\lim _{s\rightarrow \infty }\Vert d^{\unicode[STIX]{x1D70B}}w_{s}^{K}\Vert _{L^{2}(K\times S^{1})}=0$
;
$\lim _{s\rightarrow \infty }\Vert d^{\unicode[STIX]{x1D70B}}w_{s}^{K}\Vert _{L^{2}(K\times S^{1})}=0$
;(3)
 $\Vert dw_{s}^{K}\Vert _{C^{0}(K\times S^{1})}\leqslant \Vert dw\Vert _{C^{0}([0,\infty )\times S^{1})}<\infty$
.
$\Vert dw_{s}^{K}\Vert _{C^{0}(K\times S^{1})}\leqslant \Vert dw\Vert _{C^{0}([0,\infty )\times S^{1})}<\infty$
.
From (1) and (3) together with the compactness of the target manifold
![]() $M$
(which provides the uniform
$M$
(which provides the uniform
![]() $L^{2}(K\times S^{1})$
bound) and the coercive estimate for contact-instanton equation derived in [Reference Oh and WangOW2, Theorem 5.7], we obtain
$L^{2}(K\times S^{1})$
bound) and the coercive estimate for contact-instanton equation derived in [Reference Oh and WangOW2, Theorem 5.7], we obtain
for some constant
![]() $C_{K;(3,2)}$
independent of
$C_{K;(3,2)}$
independent of
![]() $s$
. Then it follows from the compactness of the embedding of
$s$
. Then it follows from the compactness of the embedding of
![]() $W^{3,2}(K\times S^{1})$
into
$W^{3,2}(K\times S^{1})$
into
![]() $C^{1,\unicode[STIX]{x1D6FC}}(K\times S^{1})$
, with
$C^{1,\unicode[STIX]{x1D6FC}}(K\times S^{1})$
, with
![]() $0<\unicode[STIX]{x1D6FC}<1$
, that the set
$0<\unicode[STIX]{x1D6FC}<1$
, that the set
![]() $\{w_{s}^{K}:K\times S^{1}\rightarrow M\}_{s\in [s_{0},\infty )}$
is sequentially compact. Therefore, for any sequence
$\{w_{s}^{K}:K\times S^{1}\rightarrow M\}_{s\in [s_{0},\infty )}$
is sequentially compact. Therefore, for any sequence
![]() $s_{k}\rightarrow \infty$
, there exists a subsequence, still denoted by
$s_{k}\rightarrow \infty$
, there exists a subsequence, still denoted by
![]() $s_{k}$
, that converges to a map
$s_{k}$
, that converges to a map
![]() $w_{\infty }^{K}\in C^{1,\unicode[STIX]{x1D6FC}}(K\times S^{1},M)$
in
$w_{\infty }^{K}\in C^{1,\unicode[STIX]{x1D6FC}}(K\times S^{1},M)$
in
![]() $C^{1,\unicode[STIX]{x1D6FC}}(K\times S^{1},M)$
as
$C^{1,\unicode[STIX]{x1D6FC}}(K\times S^{1},M)$
as
![]() $k\rightarrow \infty$
.
$k\rightarrow \infty$
.
Combined with (2), we derive the convergence
Finally by taking (1) into consideration, we also derive that both
![]() $(w_{\infty }^{K})^{\ast }\unicode[STIX]{x1D706}$
and
$(w_{\infty }^{K})^{\ast }\unicode[STIX]{x1D706}$
and
![]() $(w_{\infty }^{K})^{\ast }\unicode[STIX]{x1D706}\circ j$
are harmonic 1-forms.
$(w_{\infty }^{K})^{\ast }\unicode[STIX]{x1D706}\circ j$
are harmonic 1-forms.
Recall that these limiting maps
![]() $w_{\infty }^{K}$
have common extension
$w_{\infty }^{K}$
have common extension
![]() $w_{\infty }:\mathbb{R}\times S^{1}\rightarrow M$
by the nature of the diagonal argument which takes a sequence of compact sets
$w_{\infty }:\mathbb{R}\times S^{1}\rightarrow M$
by the nature of the diagonal argument which takes a sequence of compact sets
![]() $K$
in the way one including another and exhausting full
$K$
in the way one including another and exhausting full
![]() $\mathbb{R}$
as
$\mathbb{R}$
as
![]() $k\rightarrow \infty$
. Then
$k\rightarrow \infty$
. Then
![]() $w_{\infty }$
is
$w_{\infty }$
is
![]() $C^{1,\unicode[STIX]{x1D6FC}}$
(actually
$C^{1,\unicode[STIX]{x1D6FC}}$
(actually
![]() $C^{\infty }$
) and satisfies
$C^{\infty }$
) and satisfies
and
![]() $dw_{\infty }=(w_{\infty })^{\ast }\unicode[STIX]{x1D706}\otimes X_{\unicode[STIX]{x1D706}}$
. We also note that both
$dw_{\infty }=(w_{\infty })^{\ast }\unicode[STIX]{x1D706}\otimes X_{\unicode[STIX]{x1D706}}$
. We also note that both
![]() $(w_{\infty })^{\ast }\unicode[STIX]{x1D706}$
and
$(w_{\infty })^{\ast }\unicode[STIX]{x1D706}$
and
![]() $(w_{\infty })^{\ast }\unicode[STIX]{x1D706}\circ j$
are bounded harmonic one-forms on
$(w_{\infty })^{\ast }\unicode[STIX]{x1D706}\circ j$
are bounded harmonic one-forms on
![]() $\mathbb{R}\times S^{1}$
. Therefore, they must be written into the forms
$\mathbb{R}\times S^{1}$
. Therefore, they must be written into the forms
where
![]() $a$
,
$a$
,
![]() $b$
are some constants. Now we show that such
$b$
are some constants. Now we show that such
![]() $a$
and
$a$
and
![]() $b$
are actually related to
$b$
are actually related to
![]() ${\mathcal{T}}$
and
${\mathcal{T}}$
and
![]() ${\mathcal{Q}}$
as follows
${\mathcal{Q}}$
as follows
Lemma B.1.
Proof. Take an arbitrary point
![]() $r\in K$
. Using the
$r\in K$
. Using the
![]() $C^{1,\unicode[STIX]{x1D6FC}}$
-convergence of some sequence
$C^{1,\unicode[STIX]{x1D6FC}}$
-convergence of some sequence
![]() $w_{s_{k}}|_{\{r\}\times S^{1}}$
to
$w_{s_{k}}|_{\{r\}\times S^{1}}$
to
![]() $w_{\infty }|_{\{r\}\times S^{1}}$
, we derive
$w_{\infty }|_{\{r\}\times S^{1}}$
, we derive
 $$\begin{eqnarray}\displaystyle b=\int _{\{r\}\times S^{1}}(w_{\infty }|_{\{r\}\times S^{1}})^{\ast }\unicode[STIX]{x1D706} & = & \displaystyle \int _{\{r\}\times S^{1}}\lim _{k\rightarrow \infty }(w_{s_{k}}|_{\{r\}\times S^{1}})^{\ast }\unicode[STIX]{x1D706}\nonumber\\ \displaystyle & = & \displaystyle \lim _{k\rightarrow \infty }\int _{\{r\}\times S^{1}}(w_{s_{k}}|_{\{r\}\times S^{1}})^{\ast }\unicode[STIX]{x1D706}\nonumber\\ \displaystyle & = & \displaystyle \lim _{k\rightarrow \infty }\int _{\{r+s_{k}\}\times S^{1}}(w|_{\{r+s_{k}\}\times S^{1}})^{\ast }\unicode[STIX]{x1D706}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle b=\int _{\{r\}\times S^{1}}(w_{\infty }|_{\{r\}\times S^{1}})^{\ast }\unicode[STIX]{x1D706} & = & \displaystyle \int _{\{r\}\times S^{1}}\lim _{k\rightarrow \infty }(w_{s_{k}}|_{\{r\}\times S^{1}})^{\ast }\unicode[STIX]{x1D706}\nonumber\\ \displaystyle & = & \displaystyle \lim _{k\rightarrow \infty }\int _{\{r\}\times S^{1}}(w_{s_{k}}|_{\{r\}\times S^{1}})^{\ast }\unicode[STIX]{x1D706}\nonumber\\ \displaystyle & = & \displaystyle \lim _{k\rightarrow \infty }\int _{\{r+s_{k}\}\times S^{1}}(w|_{\{r+s_{k}\}\times S^{1}})^{\ast }\unicode[STIX]{x1D706}.\nonumber\end{eqnarray}$$
On the other hand, recalling
![]() $w^{\ast }d\unicode[STIX]{x1D706}=(1/2)|d^{\unicode[STIX]{x1D70B}}w|^{2}$
and applying Stokes’ formula and finiteness of the
$w^{\ast }d\unicode[STIX]{x1D706}=(1/2)|d^{\unicode[STIX]{x1D70B}}w|^{2}$
and applying Stokes’ formula and finiteness of the
![]() $\unicode[STIX]{x1D70B}$
-energy on
$\unicode[STIX]{x1D70B}$
-energy on
![]() $[0,\infty )\times S^{1}$
, the latter becomes
$[0,\infty )\times S^{1}$
, the latter becomes
which proves
![]() $a={\mathcal{T}}$
. On the other hand, using the closeness of
$a={\mathcal{T}}$
. On the other hand, using the closeness of
![]() $w^{\ast }\unicode[STIX]{x1D706}\circ j$
and Stokes’ formula, we easily compute
$w^{\ast }\unicode[STIX]{x1D706}\circ j$
and Stokes’ formula, we easily compute
 $$\begin{eqnarray}\displaystyle -a=\int _{\{r\}\times S^{1}}(w_{\infty }|_{\{r\}\times S^{1}})^{\ast }\unicode[STIX]{x1D706}\circ j & = & \displaystyle \int _{\{r\}\times S^{1}}\lim _{k\rightarrow \infty }(w_{s_{k}}|_{\{r\}\times S^{1}})^{\ast }\unicode[STIX]{x1D706}\circ j\nonumber\\ \displaystyle & = & \displaystyle \lim _{k\rightarrow \infty }\int _{\{r\}\times S^{1}}(w_{s_{k}}|_{\{r\}\times S^{1}})^{\ast }\unicode[STIX]{x1D706}\circ j\nonumber\\ \displaystyle & = & \displaystyle \lim _{k\rightarrow \infty }\int _{\{r+s_{k}\}\times S^{1}}(w|_{\{r+s_{k}\}\times S^{1}})^{\ast }\unicode[STIX]{x1D706}\circ j={\mathcal{Q}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle -a=\int _{\{r\}\times S^{1}}(w_{\infty }|_{\{r\}\times S^{1}})^{\ast }\unicode[STIX]{x1D706}\circ j & = & \displaystyle \int _{\{r\}\times S^{1}}\lim _{k\rightarrow \infty }(w_{s_{k}}|_{\{r\}\times S^{1}})^{\ast }\unicode[STIX]{x1D706}\circ j\nonumber\\ \displaystyle & = & \displaystyle \lim _{k\rightarrow \infty }\int _{\{r\}\times S^{1}}(w_{s_{k}}|_{\{r\}\times S^{1}})^{\ast }\unicode[STIX]{x1D706}\circ j\nonumber\\ \displaystyle & = & \displaystyle \lim _{k\rightarrow \infty }\int _{\{r+s_{k}\}\times S^{1}}(w|_{\{r+s_{k}\}\times S^{1}})^{\ast }\unicode[STIX]{x1D706}\circ j={\mathcal{Q}}.\nonumber\end{eqnarray}$$
Here in our derivation, we used Remark 9.3. This proves the lemma. ◻
By the connectedness of
![]() $[0,\infty )\times S^{1}$
, the image of
$[0,\infty )\times S^{1}$
, the image of
![]() $w_{\infty }$
is contained in a single leaf of the Reeb foliation. If
$w_{\infty }$
is contained in a single leaf of the Reeb foliation. If
![]() $\unicode[STIX]{x1D6FE}:\mathbb{R}\rightarrow M$
is a parameterization of the leaf so that it satisfies
$\unicode[STIX]{x1D6FE}:\mathbb{R}\rightarrow M$
is a parameterization of the leaf so that it satisfies
![]() $\dot{\unicode[STIX]{x1D6FE}}=X_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D6FE})$
, then we can write
$\dot{\unicode[STIX]{x1D6FE}}=X_{\unicode[STIX]{x1D706}}(\unicode[STIX]{x1D6FE})$
, then we can write
![]() $w_{\infty }(\unicode[STIX]{x1D70F},t)=\unicode[STIX]{x1D6FE}(s(\unicode[STIX]{x1D70F},t))$
, where
$w_{\infty }(\unicode[STIX]{x1D70F},t)=\unicode[STIX]{x1D6FE}(s(\unicode[STIX]{x1D70F},t))$
, where
![]() $s:\mathbb{R}\times S^{1}\rightarrow \mathbb{R}$
and
$s:\mathbb{R}\times S^{1}\rightarrow \mathbb{R}$
and
![]() $s=-{\mathcal{Q}}\,\unicode[STIX]{x1D70F}+{\mathcal{T}}\,t+c_{0}$
since
$s=-{\mathcal{Q}}\,\unicode[STIX]{x1D70F}+{\mathcal{T}}\,t+c_{0}$
since
![]() $ds=-{\mathcal{Q}}\,d\unicode[STIX]{x1D70F}+{\mathcal{T}}\,dt$
, where
$ds=-{\mathcal{Q}}\,d\unicode[STIX]{x1D70F}+{\mathcal{T}}\,dt$
, where
![]() $c_{0}$
is some constant.
$c_{0}$
is some constant.
This implies that if
![]() ${\mathcal{T}}\neq 0$
${\mathcal{T}}\neq 0$
![]() $\unicode[STIX]{x1D6FE}$
defines a closed Reeb orbit of period
$\unicode[STIX]{x1D6FE}$
defines a closed Reeb orbit of period
![]() $T$
. On the other hand, if
$T$
. On the other hand, if
![]() $T=0$
but
$T=0$
but
![]() ${\mathcal{Q}}\neq 0$
, we can only conclude that
${\mathcal{Q}}\neq 0$
, we can only conclude that
![]() $\unicode[STIX]{x1D6FE}$
is some Reeb trajectory parameterized by
$\unicode[STIX]{x1D6FE}$
is some Reeb trajectory parameterized by
![]() $\unicode[STIX]{x1D70F}\in \mathbb{R}$
.
$\unicode[STIX]{x1D70F}\in \mathbb{R}$
.
Remark B.2. Of course, if both
![]() ${\mathcal{T}}$
and
${\mathcal{T}}$
and
![]() ${\mathcal{Q}}$
vanish,
${\mathcal{Q}}$
vanish,
![]() $w_{\infty }$
is a constant map. In [Reference OhOh2], it is shown that such a puncture is a removable singularity under the finiteness of a suitably defined Hofer-type energy.
$w_{\infty }$
is a constant map. In [Reference OhOh2], it is shown that such a puncture is a removable singularity under the finiteness of a suitably defined Hofer-type energy.
Appendix C. Sobolev’s inequality for the sections of
 ${\mathcal{E}}_{1}\rightarrow \mathbb{R}$
${\mathcal{E}}_{1}\rightarrow \mathbb{R}$
In this section, we give the proof of (10.20) for the sections of the bundle
![]() ${\mathcal{E}}_{1}\rightarrow \mathbb{R}$
whose fiber is a Hilbert space possibly with infinite dimension.
${\mathcal{E}}_{1}\rightarrow \mathbb{R}$
whose fiber is a Hilbert space possibly with infinite dimension.
As in the main text, we assume
![]() ${\mathcal{E}}_{2}\subset {\mathcal{E}}_{1}$
a pair of Hilbert bundles that satisfies all the properties and is equipped with a compatible connection
${\mathcal{E}}_{2}\subset {\mathcal{E}}_{1}$
a pair of Hilbert bundles that satisfies all the properties and is equipped with a compatible connection
![]() $\unicode[STIX]{x1D6FB}$
. We denote by
$\unicode[STIX]{x1D6FB}$
. We denote by
![]() $\unicode[STIX]{x1D6F1}_{s}^{\unicode[STIX]{x1D70F}}$
the parallel transport from the fiber
$\unicode[STIX]{x1D6F1}_{s}^{\unicode[STIX]{x1D70F}}$
the parallel transport from the fiber
![]() ${\mathcal{E}}_{s}$
to
${\mathcal{E}}_{s}$
to
![]() ${\mathcal{E}}_{\unicode[STIX]{x1D70F}}$
.
${\mathcal{E}}_{\unicode[STIX]{x1D70F}}$
.
Proposition C.1. Let
![]() $I\subset \mathbb{R}$
be a closed interval and
$I\subset \mathbb{R}$
be a closed interval and
![]() $\unicode[STIX]{x1D701}:I\rightarrow {\mathcal{E}}_{2}$
be a smooth section. Then there exists
$\unicode[STIX]{x1D701}:I\rightarrow {\mathcal{E}}_{2}$
be a smooth section. Then there exists
![]() $C_{3}=C_{3}(I)>0$
depending only on the length
$C_{3}=C_{3}(I)>0$
depending only on the length
![]() $|I|$
of the interval but independent of
$|I|$
of the interval but independent of
![]() $\unicode[STIX]{x1D701}$
such that
$\unicode[STIX]{x1D701}$
such that
Proof. Thanks to (10.18), there must be a point
![]() $\unicode[STIX]{x1D70F}_{0}\in I_{k}$
such that
$\unicode[STIX]{x1D70F}_{0}\in I_{k}$
such that
where
![]() $|I|$
is the length of the interval
$|I|$
is the length of the interval
![]() $I$
. Then for any
$I$
. Then for any
![]() $\unicode[STIX]{x1D70F}\in I$
, we write
$\unicode[STIX]{x1D70F}\in I$
, we write
Therefore, we obtain
Applying the Hölder’s inequality, we derive
 $$\begin{eqnarray}\displaystyle \int _{\unicode[STIX]{x1D70F}_{0}}^{\unicode[STIX]{x1D70F}}|\unicode[STIX]{x1D6FB}_{s}\unicode[STIX]{x1D701}(s)|_{{\mathcal{E}}_{1},\unicode[STIX]{x1D70F}}\,ds & {\leqslant} & \displaystyle \sqrt{|I|}\sqrt{\int _{\unicode[STIX]{x1D70F}_{0}}^{\unicode[STIX]{x1D70F}}|\unicode[STIX]{x1D6FB}_{s}\unicode[STIX]{x1D701}(s)|_{{\mathcal{E}}_{1},\unicode[STIX]{x1D70F}}^{2}\,ds}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \sqrt{|I|}\sqrt{\int _{I}|\unicode[STIX]{x1D6FB}_{s}\unicode[STIX]{x1D701}(s)|_{{\mathcal{E}}_{1},\unicode[STIX]{x1D70F}}^{2}\,ds}\leqslant \sqrt{|I|}\,\Vert \unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D701}\Vert _{L^{2}(I,{\mathcal{E}}_{1})}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{\unicode[STIX]{x1D70F}_{0}}^{\unicode[STIX]{x1D70F}}|\unicode[STIX]{x1D6FB}_{s}\unicode[STIX]{x1D701}(s)|_{{\mathcal{E}}_{1},\unicode[STIX]{x1D70F}}\,ds & {\leqslant} & \displaystyle \sqrt{|I|}\sqrt{\int _{\unicode[STIX]{x1D70F}_{0}}^{\unicode[STIX]{x1D70F}}|\unicode[STIX]{x1D6FB}_{s}\unicode[STIX]{x1D701}(s)|_{{\mathcal{E}}_{1},\unicode[STIX]{x1D70F}}^{2}\,ds}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \sqrt{|I|}\sqrt{\int _{I}|\unicode[STIX]{x1D6FB}_{s}\unicode[STIX]{x1D701}(s)|_{{\mathcal{E}}_{1},\unicode[STIX]{x1D70F}}^{2}\,ds}\leqslant \sqrt{|I|}\,\Vert \unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D701}\Vert _{L^{2}(I,{\mathcal{E}}_{1})}\nonumber\end{eqnarray}$$
since
![]() $\unicode[STIX]{x1D70F}_{0}$
,
$\unicode[STIX]{x1D70F}_{0}$
,
![]() $\unicode[STIX]{x1D70F}\in I$
. Combining the two, we have obtained
$\unicode[STIX]{x1D70F}\in I$
. Combining the two, we have obtained
for all
![]() $\unicode[STIX]{x1D70F}\in I$
. By setting
$\unicode[STIX]{x1D70F}\in I$
. By setting
![]() $C_{3}=2\max \{\!\sqrt{|I|},1/\sqrt{|I|}\}$
, we have finished the proof.◻
$C_{3}=2\max \{\!\sqrt{|I|},1/\sqrt{|I|}\}$
, we have finished the proof.◻