Hostname: page-component-6bf8c574d5-8gtf8 Total loading time: 0 Render date: 2025-02-19T00:20:46.008Z Has data issue: false hasContentIssue false
  • English
  • Français

ANALYTIC PROPERTIES OF EISENSTEIN SERIES AND STANDARD 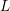$L$-FUNCTIONS

Part of: Zeta and $L$-functions: analytic theory Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  21 July 2020

OLIVER STEIN
OLIVER STEIN*
Affiliation:
Fakultät für Informatik und Mathematik, Ostbayerische Technische Hochschule Regensburg, Galgenbergstraße 32, 93053 Regensburg, Germany email oliver.stein@oth-regensburg.de
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove a functional equation for a vector valued real analytic Eisenstein series transforming with the Weil representation of 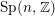$\operatorname{Sp}(n,\mathbb{Z})$ on 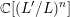$\mathbb{C}[(L^{\prime }/L)^{n}]$. By relating such an Eisenstein series with a real analytic Jacobi Eisenstein series of degree $n$, a functional equation for such an Eisenstein series is proved. Employing a doubling method for Jacobi forms of higher degree established by Arakawa, we transfer the aforementioned functional equation to a zeta function defined by the eigenvalues of a Jacobi eigenform. Finally, we obtain the analytic continuation and a functional equation of the standard 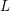$L$-function attached to a Jacobi eigenform, which was already proved by Murase, however in a different way.

MSC classification

Primary: 11F27: Theta series; Weil representation; theta correspondences 11F55: Other groups and their modular and automorphic forms (several variables) 11F66: Langlands $L$-functions; one variable Dirichlet series and functional equations 11M41: Other Dirichlet series and zeta functions
Type
Article
Information
Nagoya Mathematical Journal , Volume 244 , December 2021 , pp. 168 - 203
Check for updates
Copyright
© 2020 Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arakawa, T., Real analytic Eisenstein series for the Jacobi group , Abh. Math. Sem. Univ. Hamburg 60 (1990), 131–148.Google Scholar
Arakawa, T., Jacobi Eisenstein series and a basis problem for Jacobi forms , Comment. Math. Univ. St. Paul. 43(2) (1994), 181–216.Google Scholar
Arthur, J., Eisenstein series and the trace formula , Proc. Symp. Pure Math. 33 (1979), 27–63.Google Scholar
Asmuth, C., Weil representations of symplectic p-adic groups , Amer. J. Math. 101(4) (1979), 885–908.10.2307/2373921CrossRefGoogle Scholar
Böcherer, S., Über die funktionalgleichung automorpher L-funktionen zur siegelschen modulgruppe , J. Reine Angew. Math. 362 (1985), 146–168.Google Scholar
Bouganis, T. and Marzec, J., On the analytic properties of the standard L-function attached to Siegel–Jacobi modular forms , Doc. Math. 24 2613–2684.Google Scholar
Bruinier, J. H., Ehlen, S. and Freitag, E., Lattices with many Borchers products , Math. Comp. 85(300) (2016), 1953–1981.CrossRefGoogle Scholar
Bruinier, J. H., Funke, J. and Kudla, S., Degenerate Whittaker functions for [[()[]mml:mo lspace="1em" rspace="0em"[]()]]Sp[[()[]/mml:mo[]()]](n, ℝ) , Int. Math. Res. Not. 1 (2018), 1–56.Google Scholar
Bruinier, J. H. and Kühn, U., Integrals of automorphic Green’s functions associated to Heegner divisors , Int. Math. Res. Not. 31 (2003), 1687–1729.CrossRefGoogle Scholar
Bruinier, J. H. and Stein, O., The Weil representation and Hecke operators for vector valued modular forms , Math. Z. 264 (2010), 249–270.CrossRefGoogle Scholar
Bruinier, J. H. and Yang, T., Faltings heights of CM cycles and derivatives of L-functions , Invent. Math. 177 (2009), 631–681.10.1007/s00222-009-0192-8CrossRefGoogle Scholar
Fleig, P., Gustafsson, H., Kleinschmidt, A. and Persson, D., Eisenstein Series and Automorphic Representations. With Applications in String Theory, Cambridge Studies in Advanced Mathematics 176 , Cambridge University Press, Cambridge, 2018.CrossRefGoogle Scholar
Garrett, P., “ Pullbacks of Eisenstein series; applications ”, in Automorphic Forms of Several Variables. Taniguchi Symposium, Katata 1983, Birkhäuser, Boston, 1984, 114–137.Google Scholar
Gelbart, S. S., Weil’s Representation and the Spectrum of the Metaplectic Group, Lecture Notes in Mathematics 530 , Springer, Berlin-New York, 1976.CrossRefGoogle Scholar
Hironaka, Y. and Sato, F., Local densities of representation of quadratic forms over p-adic integers (the non-dyadic case) , J. Number Theory 83 (2000), 106–136.Google Scholar
Hörmann, F., The Weil representation and Eisenstein series, Notes, http://home.mathematik.uni-freiburg.de/hoermann/, 2015.Google Scholar
Kalinin, V. L., Eisenstein series on the symplectic group , Math. USSR-Sb. 32 (1977), 449–476.Google Scholar
Katsurada, H., An explicit formula for Siegel series , Amer. J. Math. 121(2) (1999), 415–452.CrossRefGoogle Scholar
Kedlaya, K. S., p-adic Differential Equations, Cambridge Studies in Advanced Mathematics 125 , Cambridge University Press, Cambridge, 2010.CrossRefGoogle Scholar
Kitaoka, Y., Arithmetic of Quadratic Forms, Cambridge University Press, Cambridge, 1993.10.1017/CBO9780511666155CrossRefGoogle Scholar
Kudla, S., Central derivatives of Eisenstein series and Height pairings , Ann. of Math (2) 146(3) (1997), 545–646.CrossRefGoogle Scholar
Kudla, S., “ Some Extensions of the Siegel–Weil formula ”, in Eisenstein Series and Applications, Progr. Math. 258 , Birkhäuser Boston, Boston, MA, 2008, 205–237.CrossRefGoogle Scholar
Kudla, S. and Rallis, S., On the Weil–Siegel formula , J. Reine Angew. Math. 387 (1988), 1–68.Google Scholar
Kudla, S. and Yang, T., Eisenstein series for SL(2) , Sci. China 53 (2010), 2275–2316.10.1007/s11425-010-4097-1CrossRefGoogle Scholar
Liu, Y., Arithmetic theta lifting and L-derivatives for unitary groups, I , Algebra Number Theory 5(7) (2011), 849–921.CrossRefGoogle Scholar
Liu, Y., Arithmetic theta lifting and L-derivatives for unitary groups, II , Algebra Number Theory 5(7) (2011), 923–1000.CrossRefGoogle Scholar
Miranda, R. and Morrison, D. R., Embeddings of integral quadratic forms, preprint, http://web.math.ucsb.edu/∼drm/manuscripts/eiqf.pdf.Google Scholar
Murase, A., L-functions attached to Jacobi forms of degree n, Part I. The basic identity , J. Reine Angew. Math. 401 (1989), 122–156.Google Scholar
Murase, A., L-functions attached to Jacobi forms of degree n. Part II. Functional equation , Math. Ann. 290 (1991), 247–276.CrossRefGoogle Scholar
Nguyen, A. H., Siegel theta series and the Weil representation, Diploma Thesis, Universität zu Köln, 2008.Google Scholar
Runge, B., Theta functions and Siegel–Jacobi forms , Acta Math. 175(2) (1995), 165–196.10.1007/BF02393304CrossRefGoogle Scholar
Scharlau, W., Quadratic and Hermitian forms, Grundlehren der mathematischen Wissenschaften 270 , Springer, Berlin, 1985.CrossRefGoogle Scholar
Shimura, G., Confluent hypergeometric functions on tube domains , Math. Ann. 260 (1982), 269–302.CrossRefGoogle Scholar
Stein, O., Analytic properties of the standard $L$ -function attached to a vector valued modular form, in preparation.Google Scholar
Sugano, T., Jacobi forms and the theta lifting , Comment. Math. Univ. St. Pauli 44 (1995), 1–58.Google Scholar
Weil, A., Sur certains groupes d’ operateurs unitaires , Acta Math. 111 (1964), 143–211.CrossRefGoogle Scholar
Yang, T., An explicit formula for local densities of quadratic forms , J. Number Theory 72 (1998), 309–356.CrossRefGoogle Scholar
Zhang, W., Modularity of generating functions of special cycles on Shimura varieties, Ph.D. thesis, Columbia University, 2009.Google Scholar
Ziegler, C., Jacobi forms of higher degree , Abh. Math. Sem. Univ. Hamburg 59 (1989), 191–224.CrossRefGoogle Scholar