Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-10T16:13:32.541Z Has data issue: false hasContentIssue false
  • English
  • Français

Annihilator, Completeness and Convergence of Wavelet System

Published online by Cambridge University Press:  11 January 2016

Kwok-Pun Ho
Kwok-Pun Ho*
Affiliation:
Department of Mathematics, Hong Kong University of Science and Technology, Clear Water Bay, Hong Kong, China, makho@ust.hk
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that if 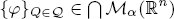is a frame and {ψＱ}Ｑ∈Q ∈ ∩ Mα(ℝn) is its dual frame (for the definition of Mα(ℝn), see Definition 2.1), where Q is the collection of dyadic cubes, then for any f ∈ S′(ℝn), there exists a sequence of polynomials, PL,L′,L″, such that

(0.1)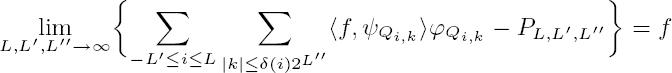

in the topology of S′(ℝn), where δ(i) = max(2i, 1). We prove this result by explicitly constructing the polynomials PL,L′,L″. Furthermore, using the above result, we assert that the linear span of the one-dimensional wavelet system is dense in a function space if and only if the dual space of this function space has an trivial intersection with the set of polynomials. This is proved by using the annihilator of the one-dimensional wavelet system.

Keywords

42B3542C1542C4046E3547B38
Type
Research Article
Information
Nagoya Mathematical Journal , Volume 188 , December 2007 , pp. 59 - 105
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 2007

References

[1] Coifman, R. and Meyer, Y., Wavelets: Calderón-Zygmund and Multilinear Operators, Cambridge studies in adv. math., #48, Cambridge Univ. Press, 1997.Google Scholar
[2] Conway, J., A Course in Functional Analysis, Graduate texts in mathematics, #96, Springer-Verlag, 1990.Google Scholar
[3] Daubechies, I., Ten Lectures on Wavelets, CBMS-NSF regional conference series in applied mathematics #61, Society for Industrial and Applied Mathematics, 1992.Google Scholar
[4] Fix, G. and Strang, G., A Fourier analysis of the finite element variational method, Construct. Aspects of Funct. Anal. (1971), 796–830.Google Scholar
[5] Frazier, M. and Jawerth, B., Decomposition of Besov spaces, Indiana Univ. Math., 34 (1985), 777–799.Google Scholar
[6] Frazier, M. and Jawerth, B., A Discrete Transform and Decomposition of Distribution Spaces, J. Funct. Anal., 93 (1990), 34–170.Google Scholar
[7] Frazier, M., Jawerth, B. and Weiss, G., Littlewood-Paley Theory and the Study of Function Spaces, CBMS Regional Conference Ser., #79, American Math. Society, 1991.Google Scholar
[8] Hernàndez, E. and Weiss, G., A first Course on Wavelets, CRC Press, 1996.CrossRefGoogle Scholar
[9] Ho, K.-P., Frame associated with Expansive Matrix Dilation, Collect. Math., 54 (2003), 217–254.Google Scholar
[10] Ho, K.-P., Remarks on Littlewood-Paley analysis, Canad. J. Math., to appear.Google Scholar
[11] Jaffard, S. and Meyer, Y., Wavelet Methods for Pointwise Regularity and Local Oscillations of Functions, Mem. Amer. Math. Soc., #123, 1996.Google Scholar
[12] Kelly, S., Kon, M. and Raphael, L., Pointwise convergence of wavelet expansions, Bull. Amer. Math. Soc. (N.S.), 30 (1994), no. 1, 87–94.CrossRefGoogle Scholar
[13] Kelly, S., Kon, M. and Raphael, L., Local convergence for wavelet expansions, J. Funct. Anal., 126 (1994), no. 1, 102–138.Google Scholar
[14] Mallat, S., A Wavelet Tour of Signal Processing, Academic Press, 1999.Google Scholar
[15] Meyer, Y., Wavelets and Operators, Cambridge studies in adv. math., #1, Cambridge Univ. Press, 1992.Google Scholar
[16] Meyer, Y., Wavelets, Vibrations and Scalings, CRM Monograph Series, #1, AMS, 1998.Google Scholar
[17] Meyer, Y., Oscillating Patterns in Image Processing and Nonlinear Evolution Equations, University Lecture Series, #1, AMS, 2001.Google Scholar
[18] Peetre, J., New thoughts on Besov spaces, Duke University Mathematics Series #1, Mathematics Depatrment, Duke University, 1976.Google Scholar
[19] Singer, I., Bases in Banach spaces I, Springer-Verlag, 1970.Google Scholar
[20] Treves, F., Topological Vector Spaces, Distributions and Kernels, Pure and Applied Maths., #1, Academic Press, 1967.Google Scholar
[21] Walnut, D., An Introduction to Wavelet Analysis, Birkhauser, 2002.Google Scholar
[22] Walter, G., Pointwise convergence of wavelet expansions, J. Approx. Theory, 80 (1995), no. 1, 108–118.Google Scholar
[23] Walter, G., Wavelets and generalized functions. Wavelets: A Tutorial in Theory and Application, Wavelet Anal. Appl., #1, Academic Press, 1992, pp. 51–70.Google Scholar
[24] Wojtaszczyk, P., A Mathematical Introduction to Wavelets, Cambridge University Press, 1997.Google Scholar
[25] Young, R., An introduction to nonharmonic Fourier series, Academic Press, 2001.Google Scholar
[26] Zayed, A., Pointwise convergence of a class of non-orthogonal wavelet expansions, Proc. Amer. Math. Soc., 128 (2000), no. 12, 3629–3637.CrossRefGoogle Scholar