Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T08:05:32.485Z Has data issue: false hasContentIssue false
  • English
  • Français

The arc-length variation of analytic capacity and a conformal geometry

Published online by Cambridge University Press:  22 January 2016

Takafumi Murai
Takafumi Murai*
Affiliation:
Department of Mathematics School of Science Nagoya University, Chikusa-ku, Nagoya, 464-01, Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a domain Ω in the extended complex plane C ∪{∞}, H∞(Ω) denotes the Banach space of bounded analytic functions in Ω with supremum norm ∥ · ∥H∞ For ζ ∈ Ω, we put

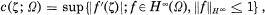
where f′(∞) = lim,z→∞z{f (∞) = f(z)} if ζ = ∞.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 125 , March 1992 , pp. 151 - 216
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1992

References

[ 1 ] Ahlfors, L., Bounded analytic functions, Duke. Math. J., 14 (1947), 1–11.CrossRefGoogle Scholar
[ 2 ] Ahlfors, L. and Beurling, A., Conformal invariants and function-theoretic null sets, Acta Math., 83 (1950), 100–134.CrossRefGoogle Scholar
[ 3 ] Baker, W. II, Kernel functions on domains with hyperelliptic double, Trans. Amer. Math. Soc, 231 (1977), 339–347.CrossRefGoogle Scholar
[ 4 ] Bergman, S., The kernel function and conformal mapping, Math. Surveys V, Amer. Math. Soc, New York, 1950.Google Scholar
[ 5 ] Davie, A., Analytic capacity and approximation problems, Trans. Amer. Math. Soc, 171 (1972), 409–444.CrossRefGoogle Scholar
[ 6 ] Fay, J. D., Theta functions on Riemann surfaces, Lecture Notes in Math. 352, Springer-Verlag, Berlin, 1973.Google Scholar
[ 7 ] Gamelin, T., Uniform Algebras, Chelsea, New York, 1984.Google Scholar
[ 8 ] Garabedian, P., Schwarz’s lemma and the Szegö kernel function, Trans. Amer. Math. Soc, 67 (1949), 1–35.Google Scholar
[ 9 ] Garabedian, P., Distortion of length in conformal mapping, Duke Math. J., 16 (1949), 439–459.CrossRefGoogle Scholar
[10] Garabedian, P. and Schiffer, M., Identities in the theory of conformal mapping, Trans. Amer. Math. Soc, 65 (1949), 187–238.CrossRefGoogle Scholar
[11] Garnett, J., Analytic capacity and measure, Lecture Notes in Math. 297, Springer-Verlag, Berlin, 1972.Google Scholar
[12] Hancock, H., Lectures on the theory of elliptic functions, Dover, New York, 1958.Google Scholar
[13] Havinson, S. Ya., Analytic capacity of sets, joint non-triviality of various classes of analytic functions and the Schwarz lemma in arbitrary domains, (Russian) Mat. Sb., 54 (1961), 3–50.Google Scholar
[14] Hejhal, D. A., Theta functions, kernel functions and Abel integrals, Mem. Amer. Math. Soc, 129 (1972).Google Scholar
[15] Komatu, Y., Conformal mapping II, (Japanese) Kyoritsu, Tokyo, 1947.Google Scholar
[16] Milne-Thomson, L. M., Theoretical hydrodynamics, Fifth edition, Macmillan, London, 1968.CrossRefGoogle Scholar
[17] Murai, T., A real variable method for the Cauchy transform, and analytic capacity, Lecture Notes in Math. 1307, Springer-Verlag, Berlin, 1988.Google Scholar
[18] Murai, T., The power 3/2 appearing in the estimate of analytic capacity, Pacific J. Math., 143 (1990), 313–340.CrossRefGoogle Scholar
[19] Murai, T., Analytic capacity for two segments, Nagoya Math. J., 122 (1991), 19–42.CrossRefGoogle Scholar
[20] Murai, T., A formula for analytic separation capacity, Kōdal Math. J., 13 (1990), 265–288.Google Scholar
[21] Nehari, Z., Conformal mapping, Dover, New York, 1952.Google Scholar
[22] Pommerenke, Ch., Über die analytische Kapazität, Arch. Math., 11 (1960), 270–277.CrossRefGoogle Scholar
[23] Sario, L. and Oikawa, K., Capacity functions, Springer-Verlag, Berlin, 1969.CrossRefGoogle Scholar
[24] Schiffer, M., On various types of orthogonalization, Duke Math. J., 17 (1950), 329–366.CrossRefGoogle Scholar
[25] Schiffer, M., Some recent developments in the theory of conformal mapping; in Courant, R., Dirichlet’s principle, 249–318, Pure Appl. Math. III, Interscience, New York, 1967.Google Scholar
[26] Schiffer, M. and Hawley, N. S., Connections and conformal mapping, Acta Math., 107 (1962), 175–274.CrossRefGoogle Scholar
[27] Schiffer, M. and Hawley, N. S., Half-order differentials on Riemann surfaces, Acta Math., 115 (1966), 199–236.Google Scholar
[28] Schiffer, M. and Spencer, D. C., Functionals of finite Riemann surfaces, Princeton Univ. Press, New Jersey, 1954.Google Scholar
[29] Smith, E. P., The Garabedian function of an arbitrary compact set, Pacific J. Math., 51 (1974), 289–300.CrossRefGoogle Scholar
[30] Suita, N., On a metric induced by analytic capacity, Kōdai Math. Sem. Rep., 25 (1973), 215–218.Google Scholar
[31] Suita, N., On a metric induced by analytic capacity II, Kōdai Math. Sem. Rep., 27 (1976), 159–162.Google Scholar
[32] Suita, N., On subadditivity of analytic capacity for two continua, Kōdai Math. J., 7 (1984), 73–75.Google Scholar
[33] Tsuji, M., Potential theory in modern function theory, Maruzen, Tokyo, 1975.Google Scholar
[34] Vitushkin, A. G., Analytic capacity of sets in problems of approximation theory, (Russian) Uspehi Mat. Nauk, 22 (1967), 141–199.Google Scholar
[35] Zalcman, L., Analytic capacity and rational approximation, Lecture Notes in Math. 50, Springer-Verlag, Berlin, 1968.Google Scholar