Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-10T17:19:51.294Z Has data issue: false hasContentIssue false
  • English
  • Français

ASYMPTOTIC EXPANSION OF THE DENSITY FOR HYPOELLIPTIC ROUGH DIFFERENTIAL EQUATION

Part of: Limit theorems Stochastic processes Stochastic analysis

Published online by Cambridge University Press:  04 November 2019

YUZURU INAHAMA  and
NOBUAKI NAGANUMA
YUZURU INAHAMA
Affiliation:
Graduate School of Mathematics, Kyushu University. 744, Motooka, Nishi-ku, Fukuoka, 819-0395, Japan email inahama@math.kyushu-u.ac.jp
NOBUAKI NAGANUMA
Affiliation:
Graduate School of Engineering Science, Osaka University. 1-3, Machikaneyama, Toyonaka, Osaka, 560-8531, Japan email naganuma@sigmath.es.osaka-u.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

We study a rough differential equation driven by fractional Brownian motion with Hurst parameter 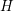$H$$(1/4<H\leqslant 1/2)$. Under Hörmander’s condition on the coefficient vector fields, the solution has a smooth density for each fixed time. Using Watanabe’s distributional Malliavin calculus, we obtain a short time full asymptotic expansion of the density under quite natural assumptions. Our main result can be regarded as a “fractional version” of Ben Arous’ famous work on the off-diagonal asymptotics.

MSC classification

Primary: 60H07: Stochastic calculus of variations and the Malliavin calculus
Secondary: 60F99: None of the above, but in this section 60G22: Fractional processes, including fractional Brownian motion
Type
Article
Information
Nagoya Mathematical Journal , Volume 243 , September 2021 , pp. 11 - 41
Check for updates
Copyright
© 2019 Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author was partially supported by JSPS KAKENHI Grant Number JP15K04922. The second author was partially supported by JSPS KAKENHI Grant Number JP17K14202.

References

Ben Arous, G., Développement asymptotique du noyau de la chaleur hypoelliptique hors du cut-locus, Ann. Sci. Éc. Norm. Sup. (4) 21(3) (1988), 307–331.Google Scholar
Boedihardjo, H., Geng, X. and Qian, Z., Quasi-sure existence of Gaussian rough paths and large deviation principles for capacities, Osaka J. Math. 53(4) (2016), 941–970.Google Scholar
Biagini, F., Hu, Y., Øksendal, B. and Zhang, T., Stochastic Calculus for Fractional Brownian Motion and Applications, Probability and its Applications (New York), Springer-Verlag London, Ltd, London, 2008.Google Scholar
Bismut, J.-M., Large Deviations and the Malliavin Calculus, Progress in Mathematics 45, Birkhäuser Boston, Inc, Boston, MA, 1984.Google Scholar
Baudoin, F., Nualart, E., Ouyang, C. and Tindel, S., On probability laws of solutions to differential systems driven by a fractional Brownian motion, Ann. Probab. 44(4) (2016), 2554–2590.Google Scholar
Baudoin, F. and Ouyang, C., Small-time kernel expansion for solutions of stochastic differential equations driven by fractional Brownian motions, Stochastic Process. Appl. 121(4) (2011), 759–792.Google Scholar
Baudoin, F., Ouyang, C. and Zhang, X., Varadhan estimates for rough differential equations driven by fractional Brownian motions, Stochastic Process. Appl. 125(2) (2015), 634–652.Google Scholar
Baudoin, F., Ouyang, C. and Zhang, X., Smoothing effect of rough differential equations driven by fractional Brownian motions, Ann. Inst. Henri Poincaré Probab. Stat. 52(1) (2016), 412–428.Google Scholar
Cass, T. and Friz, P. K., Densities for rough differential equations under Hörmander’s condition, Ann. of Math. (2) 171(3) (2010), 2115–2141.Google Scholar
Cass, T., Friz, P. K. and Victoir, N. B., Non-degeneracy of Wiener functionals arising from rough differential equations, Trans. Amer. Math. Soc. 361(6) (2009), 3359–3371.Google Scholar
Cass, T., Hairer, M., Litterer, C. and Tindel, S., Smoothness of the density for solutions to Gaussian rough differential equations, Ann. Probab. 43(1) (2015), 188–239.Google Scholar
Cass, T., Litterer, C. and Lyons, T. J., Integrability and tail estimates for Gaussian rough differential equations, Ann. Probab. 41(4) (2013), 3026–3050.Google Scholar
Coutin, L. and Qian, Z., Stochastic analysis, rough path analysis and fractional Brownian motions, Probab. Theory Related Fields 122(1) (2002), 108–140.10.1007/s004400100158Google Scholar
Driscoll, P., Smoothness of densities for area-like processes of fractional Brownian motion, Probab. Theory Related Fields 155(1–2) (2013), 1–34.10.1007/s00440-011-0389-9Google Scholar
Decreusefond, L. and Üstünel, A. S., Stochastic analysis of the fractional Brownian motion, Potential Anal. 10(2) (1999), 177–214.Google Scholar
Friz, P. K., Gess, B., Gulisashvili, A. and Riedel, S., The Jain-Monrad criterion for rough paths and applications to random Fourier series and non-Markovian Hörmander theory, Ann. Probab. 44(1) (2016), 684–738.Google Scholar
Friz, P. K. and Oberhauser, H., A generalized Fernique theorem and applications, Proc. Amer. Math. Soc. 138(10) (2010), 3679–3688.Google Scholar
Friz, P. K. and Victoir, N. B., A variation embedding theorem and applications, J. Funct. Anal. 239(2) (2006), 631–637.Google Scholar
Friz, P. K. and Victoir, N. B., Large deviation principle for enhanced Gaussian processes, Ann. Inst. Henri Poincaré Probab. Statist. 43(6) (2007), 775–785.Google Scholar
Friz, P. K. and Victoir, N. B., Multidimensional Stochastic Processes as Rough Paths: Theory and Applications, Cambridge Studies in Advanced Mathematics 120, Cambridge University Press, Cambridge, 2010.Google Scholar
Gess, B., Ouyang, C. and Tindel, S., Density bounds for solutions to differential equations driven by Gaussian rough paths, preprint, 2017, arXiv:1712.02740.Google Scholar
Hairer, M. and Pillai, N. S., Ergodicity of hypoelliptic SDEs driven by fractional Brownian motion, Ann. Inst. Henri Poincaré Probab. Stat. 47(2) (2011), 601–628.Google Scholar
Hairer, M. and Pillai, N. S., Regularity of laws and ergodicity of hypoelliptic SDEs driven by rough paths, Ann. Probab. 41(4) (2013), 2544–2598.10.1214/12-AOP777Google Scholar
Hu, Y. and Tindel, S., Smooth density for some nilpotent rough differential equations, J. Theoret. Probab. 26(3) (2013), 722–749.Google Scholar
Hu, Y., Analysis on Gaussian Spaces, World Scientific Publishing Co. Pte. Ltd, Hackensack, NJ, 2017.Google Scholar
Inahama, Yuzuru, A stochastic Taylor-like expansion in the rough path theory, J. Theoret. Probab. 23(3) (2010), 671–714.Google Scholar
Inahama, Y., Malliavin differentiability of solutions of rough differential equations, J. Funct. Anal. 267(5) (2014), 1566–1584.Google Scholar
Inahama, Y., Short time kernel asymptotics for Young SDE by means of Watanabe distribution theory, J. Math. Soc. Japan 68(2) (2016), 535–577.Google Scholar
Inahama, Y., Short time kernel asymptotics for rough differential equation driven by fractional Brownian motion, Electron. J. Probab. 21(34) (2016), 29 pp.Google Scholar
Ikeda, N. and Watanabe, S., Stochastic Differential Equations and Diffusion Processes, 2nd ed., North-Holland Mathematical Library 24, North-Holland Publishing Co, Amsterdam, 1989, Kodansha, Ltd., Tokyo.Google Scholar
Lyons, T. J., Caruana, M. and Lévy, T., Differential Equations Driven by Rough Paths, Lecture Notes in Mathematics 1908, Springer, Berlin, 2007, Lectures from the 34th Summer School on Probability Theory held in Saint-Flour, July 6–24, 2004, With an introduction concerning the Summer School by Jean Picard.Google Scholar
Lyons, T. J. and Qian, Z., System Control and Rough Paths, Oxford Mathematical Monographs, Oxford University Press, Oxford, 2002, Oxford Science Publications.Google Scholar
Matsumoto, H. and Taniguchi, S., Stochastic Analysis, Itô and Malliavin Calculus in Tandem, Japanese ed., Cambridge Studies in Advanced Mathematics 159, Cambridge University Press, Cambridge, 2017.Google Scholar
Nualart, D., The Malliavin Calculus and Related Topics, 2nd ed., Probability and its Applications (New York), Springer, Berlin, 2006.Google Scholar
Shigekawa, I., Stochastic Analysis, Translations of Mathematical Monographs 224, American Mathematical Society, Providence, RI, 2004, Translated from the 1998 Japanese original by the author, Iwanami Series in Modern Mathematics.Google Scholar
Watanabe, S., Analysis of Wiener functionals (Malliavin calculus) and its applications to heat kernels, Ann. Probab. 15(1) (1987), 1–39.Google Scholar