Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kim, Seung Won
and
Lee, Jong Bum
2007.
Averaging formula for Nielsen coincidence numbers.
Nagoya Mathematical Journal,
Vol. 186,
Issue. ,
p.
69.
LEE, Jong Bum
and
ZHAO, Xuezhi
2007.
Homotopy minimal periods for expanding maps on infra-nilmanifolds.
Journal of the Mathematical Society of Japan,
Vol. 59,
Issue. 1,
Lee, Jong Bum
and
Lee, Kyung Bai
2009.
Averaging Formula for Nielsen Numbers of Maps on Infra-Solvmanifolds of Type (R).
Nagoya Mathematical Journal,
Vol. 196,
Issue. ,
p.
117.
Dekimpe, Karel
and
Penninckx, Pieter
2010.
Coincidence theory for infra-nilmanifolds.
Topology and its Applications,
Vol. 157,
Issue. 10-11,
p.
1815.
Liang, Zhibin
and
Zhao, Xuezhi
2012.
Self-maps on flat manifolds with infinitely many periods.
Discrete & Continuous Dynamical Systems - A,
Vol. 32,
Issue. 6,
p.
2223.
Ha, Ku Yong
Lee, Jong Bum
and
Penninckx, Pieter
2012.
Formulas for the Reidemeister, Lefschetz and Nielsen coincidence number of maps between infra-nilmanifolds.
Fixed Point Theory and Applications,
Vol. 2012,
Issue. 1,
Heath, Philip R.
2015.
Groupoids and relations among Reidemeister and among Nielsen numbers.
Topology and its Applications,
Vol. 181,
Issue. ,
p.
3.
Brown, Robert F.
2015.
Construction of multiply fixed n-valued maps.
Topology and its Applications,
Vol. 196,
Issue. ,
p.
249.
Fel'shtyn, Alexander
and
Lee, Jong Bum
2015.
The Nielsen and Reidemeister numbers of maps on infra-solvmanifolds of type (R).
Topology and its Applications,
Vol. 181,
Issue. ,
p.
62.
Zhang, Baoqun
and
Zhao, Xuezhi
2017.
Difference cochains and Reidemeister traces.
Chinese Annals of Mathematics, Series B,
Vol. 38,
Issue. 6,
p.
1365.
Jiang, Bo Ju
and
Zhao, Xue Zhi
2018.
Some developments in Nielsen fixed point theory.
Acta Mathematica Sinica, English Series,
Vol. 34,
Issue. 1,
p.
91.
Lee, Jong Bum
and
Yoo, Won Sok
2019.
Algebraic Topology and Related Topics.
p.
177.
Yoo, Won Sok
2020.
The R∞ property for crystallographic groups of Sol14.
Journal of Algebra and Its Applications,
Vol. 19,
Issue. 04,
p.
2050072.
Li, Changbok
2021.
Calculation of Nielsen periodic numbers on infra-nilmanifolds.
Topology and its Applications,
Vol. 302,
Issue. ,
p.
107839.
Ha, Ku Yong
Lee, Jong Bum
and
Yoo, Won Sok
2023.
The Reidemeister numbers and the Hirsch ranks for preimage subgroups.
Journal of Fixed Point Theory and Applications,
Vol. 25,
Issue. 1,
Dekimpe, Karel
and
van Den Bussche, Iris
2023.
An averaging formula for Nielsen numbers on infra-solvmanifolds.
Journal of Fixed Point Theory and Applications,
Vol. 25,
Issue. 1,
Li, Changbok
2023.
Calculation of Nielsen periodic numbers on infra-solvmanifolds of type (R).
Topology and its Applications,
Vol. 330,
Issue. ,
p.
108487.
Li, Changbok
2024.
Calculation of Nielsen periodic numbers on infra-solvmanifolds.
Topology and its Applications,
Vol. 357,
Issue. ,
p.
109073.
Dekimpe, Karel
and
De Weerdt, Lore
2024.
An Averaging Formula for Nielsen Numbers of Affine n-Valued Maps on Infra-Nilmanifolds.
Bulletin of the Brazilian Mathematical Society, New Series,
Vol. 55,
Issue. 4,
Dekimpe, Karel
and
De Weerdt, Lore
2025.
Averaging formulas for the Reidemeister trace, Lefschetz and Nielsen numbers of n-valued maps.
Journal of Fixed Point Theory and Applications,
Vol. 27,
Issue. 2,

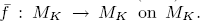 . We prove a question raised by McCord, which is for any
. We prove a question raised by McCord, which is for any 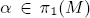 with
with 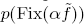 an essential fixed point class, fix
an essential fixed point class, fix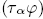 =1. As a consequence, we obtain the following averaging formula for Nielsen numbers
=1. As a consequence, we obtain the following averaging formula for Nielsen numbers